标签:

前面两章中讲到的SVM的求解方式都是基于这样一个前提:我们最终求得的直线或者曲线都能把两种不同的分完完全全得区分开来,就是所谓的Hard-Margin,但是这样的方式有时候就会造成过拟合,如上图所示,因为这样的方式并不能把那些所谓的噪声给屏蔽掉.

为了抵消这些噪声的影响,我们在Hard-Margin的基础上增加了一项,这一项表示的是拟合的结果跟yn不一致的情况.同时改变了约束条件,对于能够正确拟合那些点,我们还是要求其能够满足
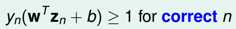
但是对于那些是噪声的点,我们就不加任何约束了.
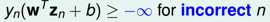

所以,这里最后需要求最优解的式子就变成了上图黄色方框中的式子,但是这个式子并不是线性的,所以不能用QP来求解.
同时我们注意到之前提到的Dual和Kernel方法都不能把small error和large error,也就是这些犯错的点距离margin边界有多远,描述出来.

所以最后我们引入了一个参数,这个参数表示的是每一个训练的点违反margin的要求有多少,然后把我们需要求解的方程和约束表示成了上述的例子.

上图中就把margin violation这个概念在图中画出来了,violation指的就是该点距离margin boundary的大小.同时C越大,就要求这个violation就越小.
接下去就是怎么解这个方程的问题了.这里我们采用Dual SVM里用过了拉格朗日乘数法来进行求解.

所以我们将方程写成拉格朗日乘式,把两个约束条件都加了进去.

这里先对En求导,得到an和bn之间的关系,然后根据约束条件,把bn的约束移除,之后把En也从式子中消去了.
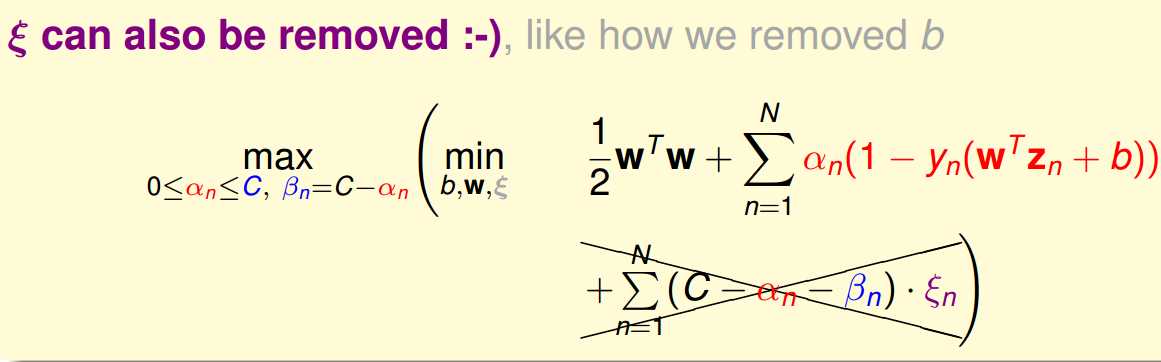

所以最后的式子跟Hard-Margin中SVM的表达方式基本一样,只是an多了一个对其上限的要求.

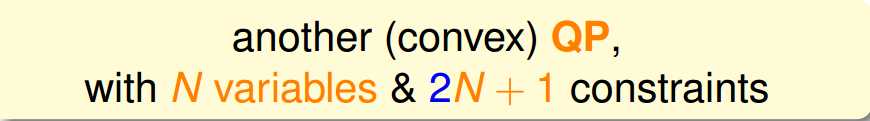
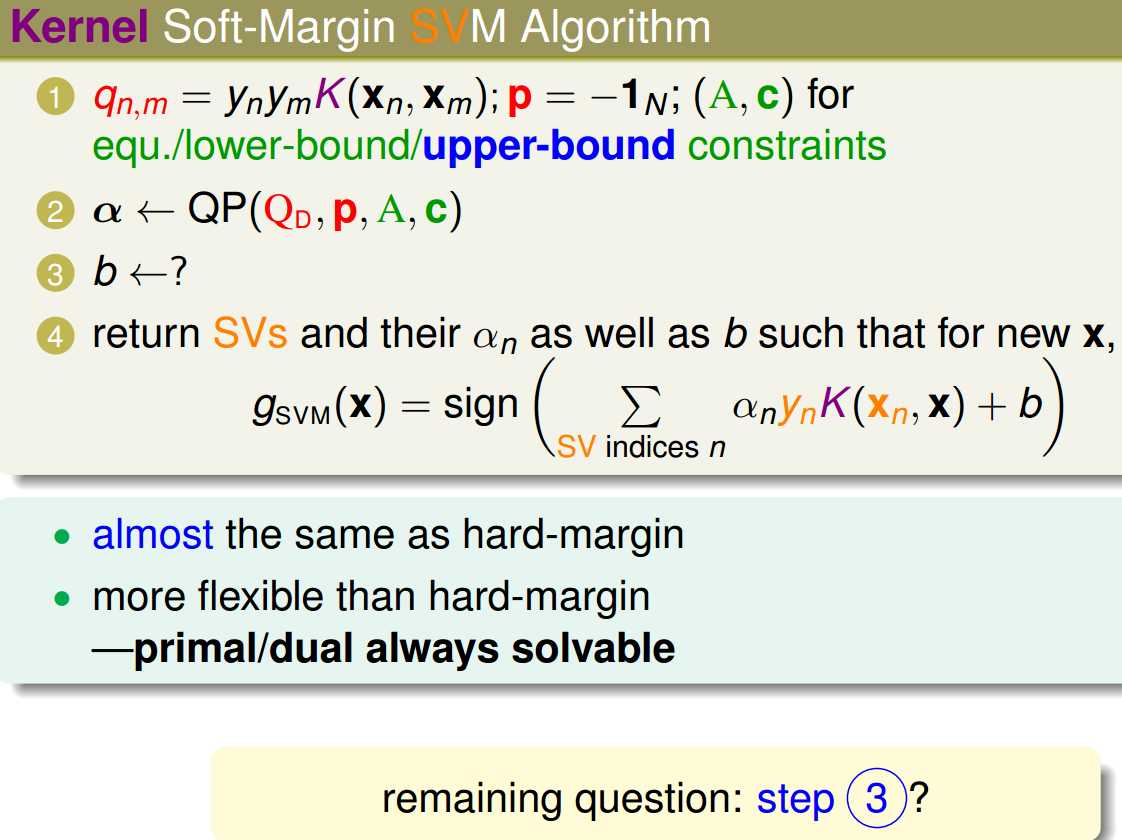
我们把他写成用kernel进行求解的过程,基本上跟hard-margin的求解过程一致,然后再来看看b的求解.

之前对hard-margin SVM进行求解的时候,最后只取an>0的一个点,然后求出相应的b, 对于soft-margin的b进行求解的时候,如果只要求an>0, 那么式子中还有一项未知, 再加上 an<C的条件,才能把b求出来.那么这些an代表的就是在margin boundary上而且没有margin violation的那些SV.
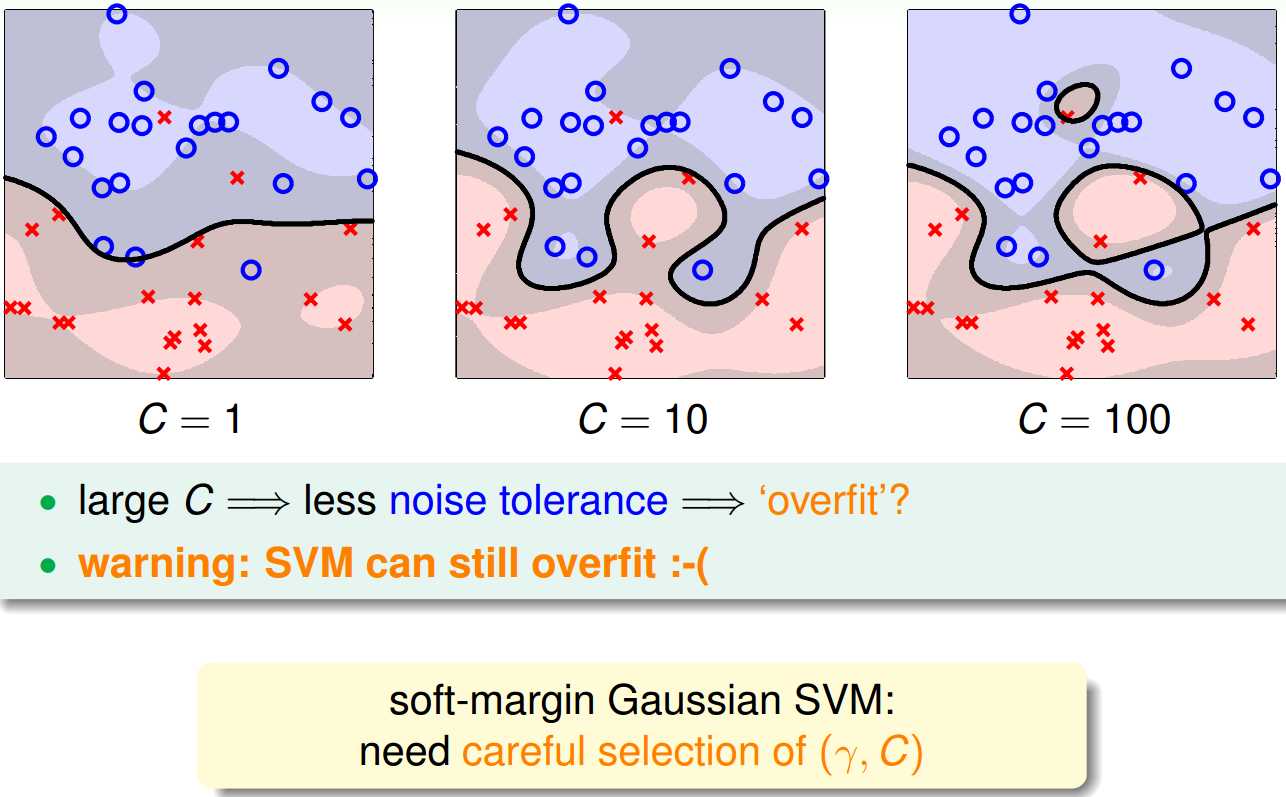
上图就是说soft-margin SVM还是有可能会过拟合的,所以还是要小心地去选取这些参数.
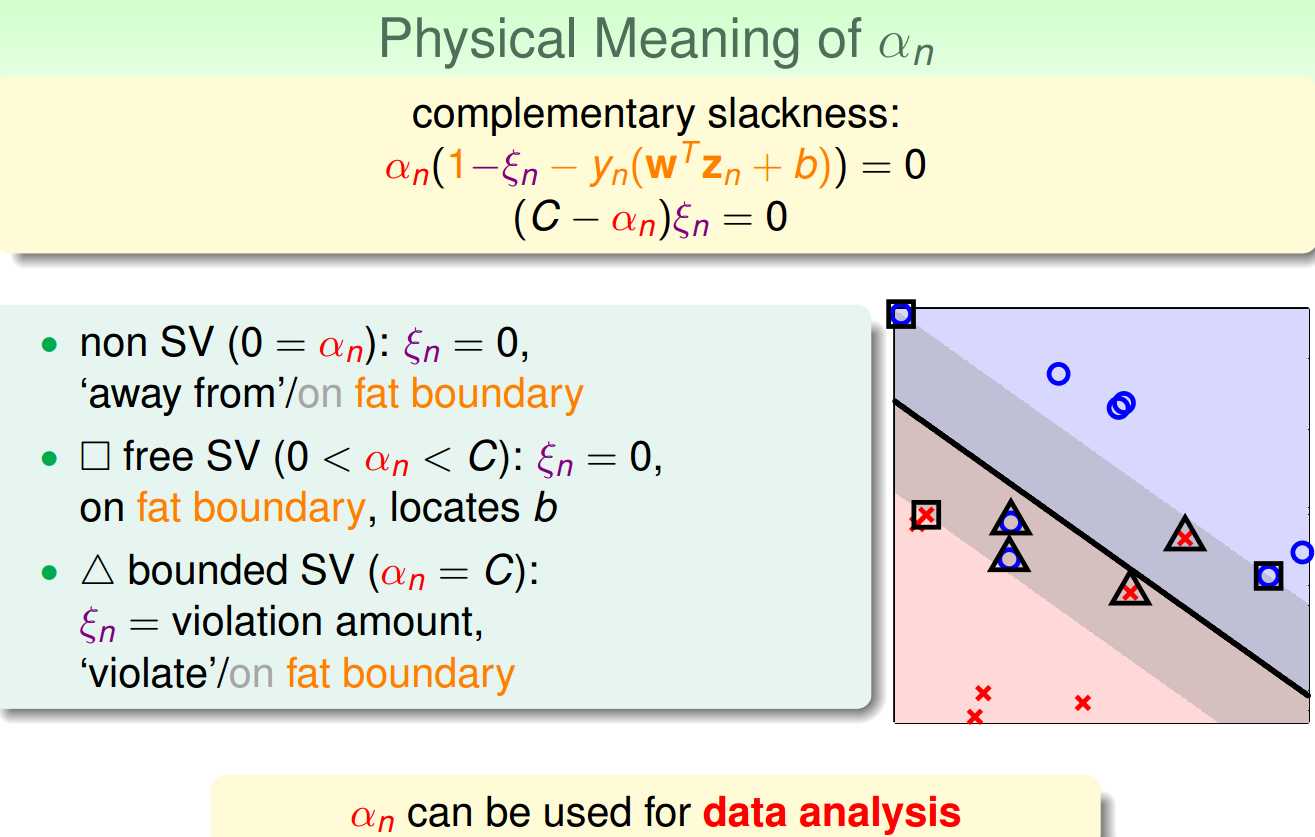
上图中就把不同an所对应的图像上的意义表示了出来,其中an=0的话就是说,没有violation,这些点都是远离margin boundary或者在上面的点.(圆形)
0<an<C的那些点就是落在margin boundary上的那些点.(正方形)
an=C的话就是在margin boundary里面违反了margin 要求的那些点(三角形)
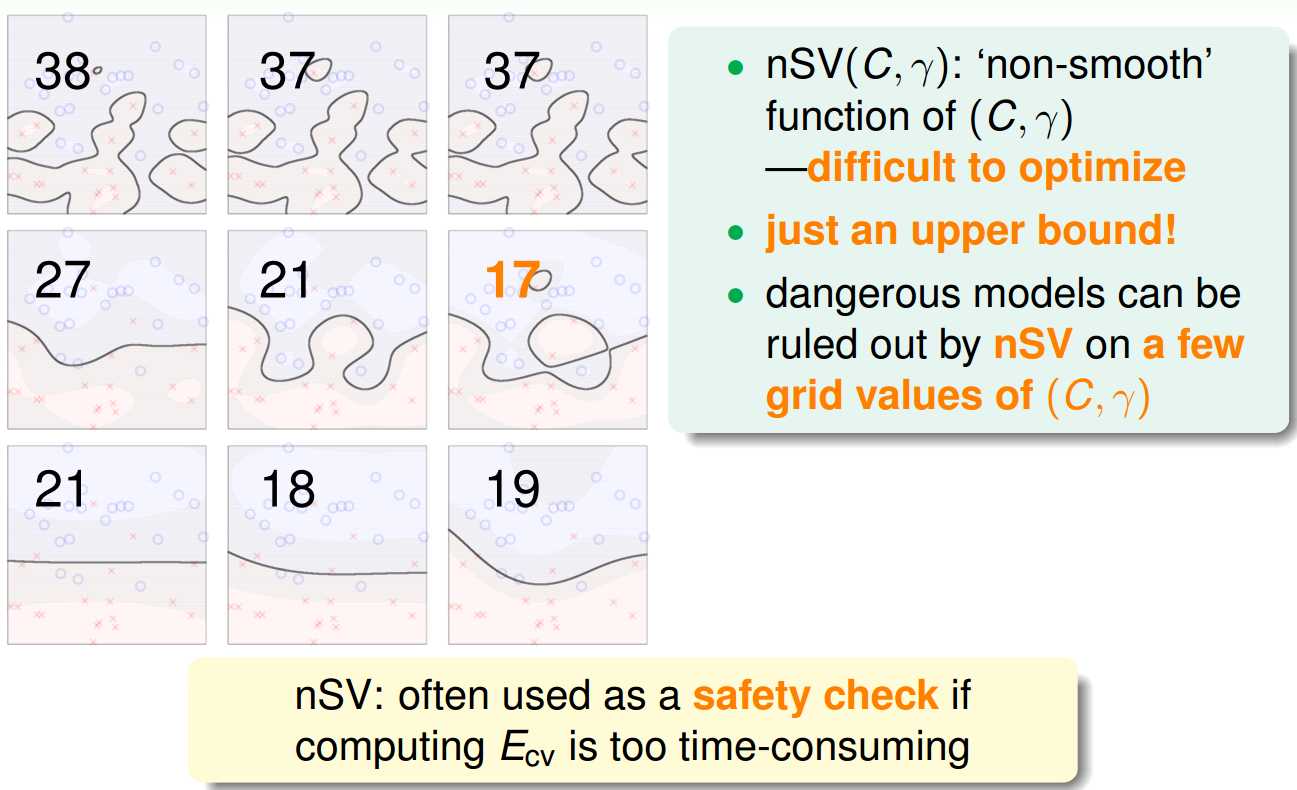
最后,Eloocv给出了一个用于估算Ecv的一个上界,公式表示这个上界跟SV的数量有关,证明的思路就是说如果(Xn,Yn)不是SV,其an=0,那么当去掉(Xn,Yn)的时候,最终得到的a1,a2…,an也依然是优的解,不会改变.这个结论通常可以在Cross Validation中用来估计该情形下的Ecv.

总结:


上图中,我们把原先的约束条件用max里面的函数替换掉,于是本来是有约束的形式变成了没有约束条件的形式.

这样我们就看到了SVM的没有约束条件的形式就跟之前我们在做L2 Regularization的时候得到的形式很接近了,一方面我们希望最后得到的w足够短,另一方面又希望得出的Err足够小,但是我们得到的Unconstrained Form有两个问题:一个是QP不适用,另一方面max无法微分,所以解起来有困难.

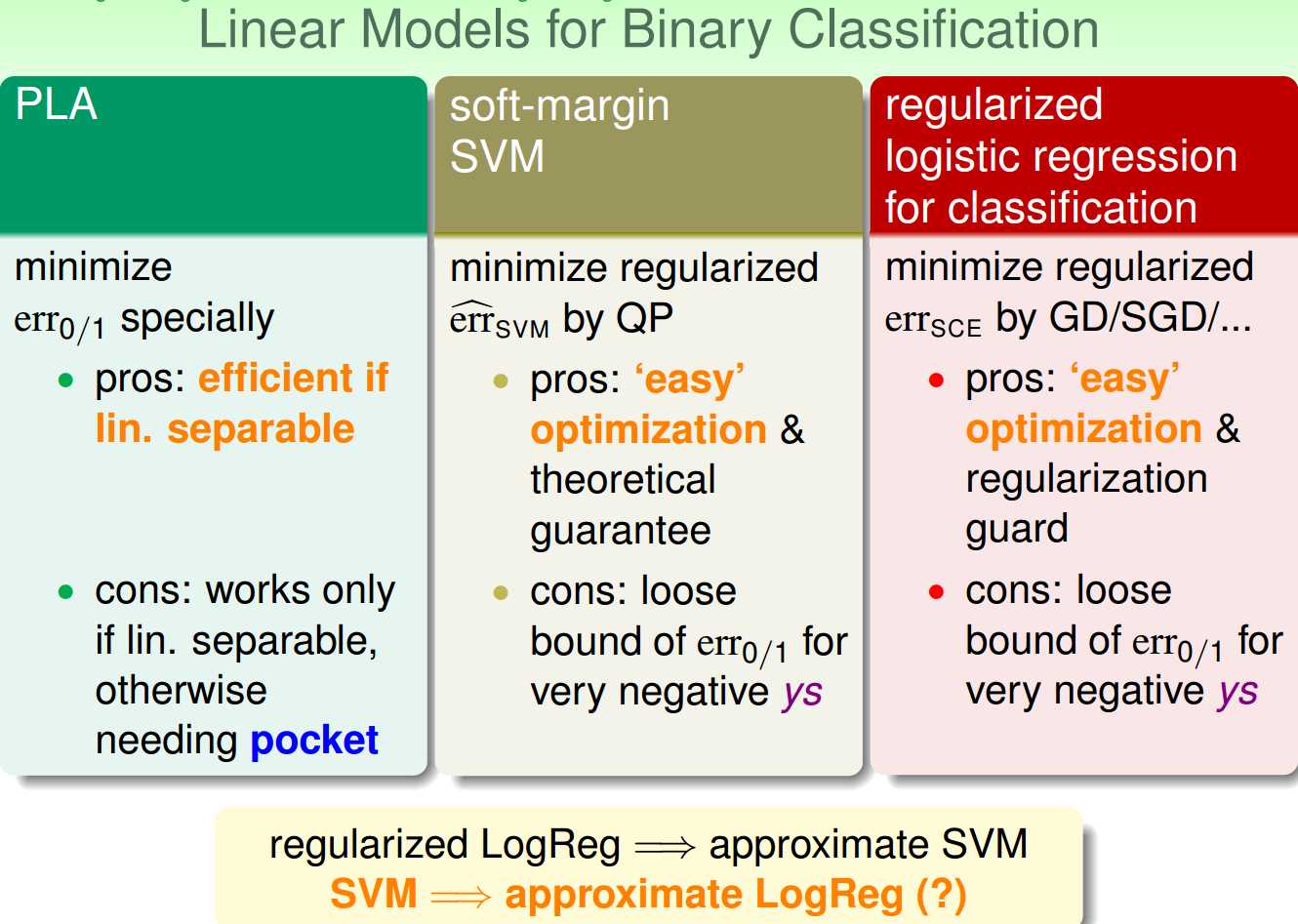
上图比较了四种学习模型的形式,指出了四种模型之间的联系

接下去我们在类比下Pocket Model, SVM和Logistic Regression之间在Err上的联系,从图像上看到,SVM和Logistic Regression在ys很小的时候,得到的Err的upper bound都很大,在ys很大的时候,Err都趋向于零.
所以,SVM和L2-regularized logistic regression是很类似的.
标签:
原文地址:http://www.cnblogs.com/enzyme/p/5764753.html