poj1840

标签：

Description

Input

Output

Sample Input

37 29 41 43 47

Sample Output

654

Source

大致题意：

给出一个5元3次方程，输入其5个系数，求它的解的个数

其中系数 ai∈[-50,50]  自变量xi∈[-50,0）∪（0,50]

注意：

  若x1 =a, x2=b ,x3=c ,x4=d,x5=e时，与 x1=b, x2=a ,x3=c ,x4 =d, x5=e 代入方程后都得到值0，那么他们视为不同的解。

解题思路：

直观的思路：暴力枚举，O(n^5)

题目Time Limit=5000ms，1ms大约可以执行1000条语句，那么5000ms最多执行500W次

每个变量都有100种可能值，那么暴力枚举，5层循环，就是要执行100^5=100E次，等着TLE吧。。。。

要AC这题，就要对方程做一个变形

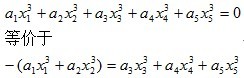
即先枚举x1和x2的组合，把所有出现过的 左值 记录打表，然后再枚举x3 x4 x5的组合得到的 右值，如果某个右值等于已经出现的左值，那么我们就得到了一个解

时间复杂度从 O(n^5)降低到 O(n^2+n^3)，大约执行100W次

我们先定义一个映射数组hash[]，初始化为0

对于方程左边，当x1=m  ,  x2= n时得到sum，则把用hash[]记录sum : hash[sum]++，表示sum这个值出现了1次

之所以是记录“次数”，而不是记录“是否已出现”，

是因为我们不能保证函数的映射为 1对1 映射，更多的是存在 多对1映射。

例如当 a1=a2时，x1=m  ,  x2= n我们得到了sum，但x1=n  ,  x2= m时我们也会得到sum，但是我们说这两个是不同的解，这就是 多对1 的情况了，如果单纯记录sum是否出现过，则会使得 解的个数 减少。

其次，为了使得 搜索sum是否出现 的操作为o(1)，我们把sum作为下标，那么hash数组的上界就取决于a1 a2 x1 x2的组合，四个量的极端值均为50

因此上界为 50*50^3+50*50^3=12500000，由于sum也可能为负数，因此我们对hash[]的上界进行扩展，扩展到25000000，当sum<0时，我们令sum+=25000000存储到hash[]

由于数组很大，必须使用全局定义

同时由于数组很大，用int定义必然会MLE，因此要用char或者short定义数组，推荐short

一遍过。 

AC代码：

#include<cstdio>
#include<cstring>
using namespace std;
#define N 25000000
#define t 50
int a1,a2,a3,a4,a5;
short hash[N+1];
int main(){
	while(scanf("%d%d%d%d%d",&a1,&a2,&a3,&a4,&a5)==5){
		memset(hash,0,sizeof hash);
		for(int x1=-t;x1<=t;x1++){
			if(!x1) continue;
			for(int x2=-t;x2<=t;x2++){
				if(!x2) continue;
				int sum=(a1*x1*x1*x1+a2*x2*x2*x2)*(-1);
				if(sum<0) sum+=N;
				hash[sum]++;
			}
		}
		int ans=0;
		for(int x3=-t;x3<=t;x3++){
			if(!x3) continue;
			for(int x4=-t;x4<=t;x4++){
				if(!x4) continue;
				for(int x5=-t;x5<=t;x5++){
					if(!x5) continue;
					int sum=(a3*x3*x3*x3+a4*x4*x4*x4+a5*x5*x5*x5);
				    if(sum<0) sum+=N;
				    if(hash[sum])
					ans+=hash[sum];
				}
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}

poj1840

标签：

原文地址：http://www.cnblogs.com/shenben/p/5765885.html