标签:
1、小波分析的发展
在传统的傅里叶分析中,信号完全是在频域展开的,不包含任何时域的信息,因为信号的频域非常重要,这样的处理对某些领域来说是很恰当的。但其丢弃的时域信息对于某些领域来说同样的很重要,,所以人们对傅里叶变换进行了推广,提出了很多能表征时域和频域信息的嘻哈处理方法。如短时傅里叶变换,Gabor变换,时频分析,小波变换等。
短时傅里叶变换只能在一个分辨率上进行,对很多应用来说不够精确,存在很大缺陷。小波分析克服了短时傅里叶变换在单分辨率上的缺陷,具有多分辨率分析的特点。在时域和频域都有表征信号局部信息的能力,时间窗和频率窗都可以根据信号的具体形态来动态调整。
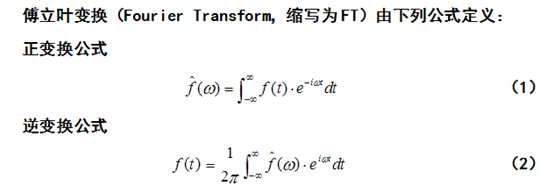
加窗傅里叶变换:
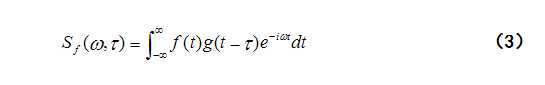
小波变换:
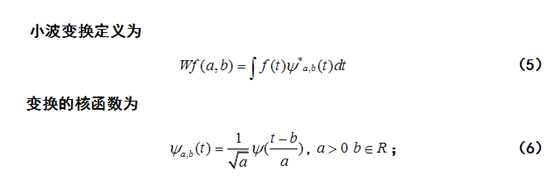
小波变换的公式有内积形式和卷积形式,两种形式的实质都是一样的.它要求的就是一个个小波分量的系数也就是"权"。其直观意义就是首先用一个时窗最窄,频窗最宽的小波作为尺子去一步步地"量"信号,也就是去比较信号与小波的相似程度.信号局部与小波越相似,则小波变换的值越大,否则越小!当一步比较完成后,再将尺子拉长一倍,又去一步步地比较,从而得出一组组数据.如此这般循环,最后得出的就是信号的小波分解(小波级数)。
2、信号的分解
傅里叶级数将周期信号分解为了一个个倍频分量的叠加,基函数是正交的,也就是通常所说的标准正交基.通过分解我们就能将特定的频率成分提取出来而实现特定的各种需要,如滤波,消噪等,傅里叶变换则将倍频谱转换为了连续谱,其意义差不多.小波变换也是一种信号分解思想:只不过它是将信号分解为一个个频带信号的叠加.其中的低频部分作为信号的近似,高频部分作为信号的细节.所谓的细节部分就是一组组小波分量的叠加,也就是常说的小波级数。
3、尺度函数与小波函数
小波函数是由尺度函数构造的,尺度函数的性质决定了小波函数的性质。尺度函数从滤波器的角度看是低通滤波器,而小波函数是高通滤波器。尺度函数又称为小波父函数.根据双尺度方程,可以由尺度函数生成小波.进行信号处理时,先要对信号进行副近.也就是用尺度函数对信号进行分解.尺度函数的频带与待分析信号的频带相同,然后将逼近函数分别在尺度空间和小波空间中进行分解.就得到了信号的低频粗略部分和高频细节部分.此时新的尺度函数频带是原信号频带的一半.小波函数的频带是另一半(高频部分).由此实现了对原信号的按频带分解!
4、小波分析与傅里叶分析的比较
小波分析可以说是一种广义上的傅里叶分析,小波分析的存在性证明,小波基的构造及结果分析都以来傅里叶分析,两者相辅相成,比较后有以下特点:
(1)傅里叶分析实质是吧能量有限的信号f(t)分解到{ejwt}为正交基的空间上去;小波分析的实质是吧能量有限的信号f(t)分解到W-j(j=1,2,…J)和W-j所构成的空间上去。
(2)傅里叶用到的基函数只有sin(wt),cos(wt),exp(jwt),具有唯一性;小波用到的函数则不具有我唯一性,同一个工程用不同的小波函数分析有时结果相差甚远,小波函数的选取是小波分析应用中的一个难题,目前往往通过经验和不断实验来选择小波函数。
(3)在频域中,傅里叶分析具有具有良好的局部化能力,特别是对于那些频率成分比较简单的确定性信号,傅里叶分析很容易把信号表示成各频率成分叠加和形式,但是在时域中,傅里叶分析没有局部化能力,即无法从信号f(t)的傅里叶分析F(W)中看出f(t)任一时间点附近的形态。因为F(W)是关于w的谐波分量的振幅,在傅里叶展开形式中,它是由f(t)的整体形态决定的。
(4)在小波分析尺度中,尺度a的 值越大,傅里叶分析中w的值越小。
(5)如果用信号通过滤波器来解释,他们的不同之处在于:对短时傅里叶变换,带通滤波器的带宽与中心频率无关,相反,小波分析带通滤波器的带宽则正比于中心频率,称之为等Q结构(Q为滤波器的品质因数)。
标签:
原文地址:http://www.cnblogs.com/WJ-0808/p/5766801.html