标签:
首先我们来看一个线性回归的问题,在下面的例子中,我们选取不同维度的特征来对我们的数据进行拟合。
对于上面三个图像做如下解释:
选取一个特征 ,
, 来拟合数据,可以看出来拟合情况并不是很好,有些数据误差还是比较大
来拟合数据,可以看出来拟合情况并不是很好,有些数据误差还是比较大
针对第一个,我们增加了额外的特征 ,
, ,这时我们可以看出情况就好了很多。
,这时我们可以看出情况就好了很多。
这个时候可能有疑问,是不是特征选取的越多越好,维度越高越好呢?所以针对这个疑问,如最右边图,我们用5揭多项式使得数据点都在同一条曲线上,为![]() 。此时它对于训练集来说做到了很好的拟合效果,但是,我们不认为它是一个好的假设,因为它不能够做到更好的预测。
。此时它对于训练集来说做到了很好的拟合效果,但是,我们不认为它是一个好的假设,因为它不能够做到更好的预测。
针对上面的分析,我们认为第二个是一个很好的假设,而第一个图我们称之为欠拟合(underfitting),而最右边的情况我们称之为过拟合(overfitting)
所以我们知道特征的选择对于学习算法的性能来说非常重要,所以现在我们要引入局部加权线性回归,它使得特征的选择对于算法来说没那么重要,也就是更随性了。
在我们原始的线性回归中,对于输入变量 ,我们要预测,通常要做:
,我们要预测,通常要做:
而对于局部加权线性回归来说,我们要做:
 为权值,从上面我们可以看出,如果
为权值,从上面我们可以看出,如果 很大,我们将很难去使得
很大,我们将很难去使得 小,所以如果
小,所以如果 很小,则它所产生的影响也就很小。
很小,则它所产生的影响也就很小。
通常我们选择 的形式如下所示:
的形式如下所示:
上式中参数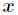 为新预测的样本特征数据,它是一个向量,参数
为新预测的样本特征数据,它是一个向量,参数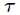 控制了权值变化的速率,
控制了权值变化的速率, 和
和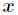 的图像如下
的图像如下
可以看到
(1)如果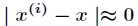 ,则
,则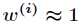 。
。
(2)如果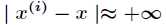 ,则
,则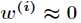 。
。
也即,离 很近的样本,权值接近于1,而对于离
很近的样本,权值接近于1,而对于离 很远的样本,此时权值接近于0,这样就是在
很远的样本,此时权值接近于0,这样就是在 局部构成线性回归,它依赖的也只是
局部构成线性回归,它依赖的也只是 周边的点
周边的点
图中红色直线使用线性回归做的结果,黑色直线使用LWR做的结果,可以看到局部加权回归的效果较好。
注意:
的形式跟高斯函数很像,但是它和高斯函数一点关系都没有,
是波长参数,
越大远距离样本权值下降更快。
局部加权回归在每一次预测新样本时都会重新的确定参数,从而达到更好的预测效果当数据规模比较大的时候计算量很大,学习效率很低。并且局部加权回归也不是一定就是避免underfitting。
对于线性回归算法,一旦拟合出适合训练数据的参数θi’s,保存这些参数θi’s,对于之后的预测,不需要再使用原始训练数据集,所以是参数学习算法。
对于局部加权线性回归算法,每次进行预测都需要全部的训练数据(每次进行的预测得到不同的参数θi’s),没有固定的参数θi’s,所以是非参数算法。
局部加权线性回归(Locally weighted linear regression)
标签:
原文地址:http://www.cnblogs.com/czdbest/p/5767138.html