标签:
二叉查找树(BST)是二叉树的一个重要的应用,它在二叉树的基础上加上了这样的一个性质:对于树中的每一个节点来说,如果有左儿子的话,它的左儿子的值一定小于它本身的值,如果有右儿子的话,它的右儿子的值一定大于它本身的值。
二叉查找树的操作一般有插入、删除和查找,这几个操作的平均时间复杂度都为O(logn),插入和查找操作很简单,删除操作会复杂一点,除此之外,因为二叉树的中序遍历是一个有序序列,我就额外加上了一个中序遍历操作。
二叉查找树的应用不是很多,因为它最坏的时候跟线性表差不多,大部分会应用到它的升级版,平衡二叉树和红黑树,这两棵树都能把时间复杂度稳定在O(logn)左右。虽然不会用到,但是二叉查找树是一定要学好的,毕竟它是平衡二叉树和红黑树的基础。
完整代码:
//二叉查找树节点信息 template<class T> class TreeNode { public: TreeNode():lson(NULL),rson(NULL),freq(1){} T data;//值 unsigned int freq;//频率 TreeNode* lson;//指向左儿子的坐标 TreeNode* rson;//指向右儿子的坐标 }; //二叉查找树类的属性和方法声明 template<class T> class BST { private: TreeNode<T>* root;//根节点 void insertpri(TreeNode<T>* &node,T x);//插入 TreeNode<T>* findpri(TreeNode<T>* node,T x);//查找 void insubtree(TreeNode<T>* node);//中序遍历 void Deletepri(TreeNode<T>* &node,T x);//删除 public: BST():root(NULL){} void insert(T x);//插入接口 TreeNode<T>* find(T x);//查找接口 void Delete(T x);//删除接口 void traversal();//遍历接口 }; //插入 template<class T> void BST<T>::insertpri(TreeNode<T>* &node,T x) { if(node==NULL)//如果节点为空,就在此节点处加入x信息 { node=new TreeNode<T>(); node->data=x; return; } if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中插入x { insertpri(node->lson,x); } else if(node->data<x)//如果x大于节点的值,就继续在节点的右子树中插入x { insertpri(node->rson,x); } else ++(node->freq);//如果相等,就把频率加1 } //插入接口 template<class T> void BST<T>::insert(T x) { insertpri(root,x); } //查找 template<class T> TreeNode<T>* BST<T>::findpri(TreeNode<T>* node,T x) { if(node==NULL)//如果节点为空说明没找到,返回NULL { return NULL; } if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中查找x { return findpri(node->lson,x); } else if(node->data<x)//如果x大于节点的值,就继续在节点的左子树中查找x { return findpri(node->rson,x); } else return node;//如果相等,就找到了此节点 } //查找接口 template<class T> TreeNode<T>* BST<T>::find(T x) { return findpri(root,x); } //删除 template<class T> void BST<T>::Deletepri(TreeNode<T>* &node,T x) { if(node==NULL) return ;//没有找到值是x的节点 if(x < node->data) Deletepri(node->lson,x);//如果x小于节点的值,就继续在节点的左子树中删除x else if(x > node->data) Deletepri(node->rson,x);//如果x大于节点的值,就继续在节点的右子树中删除x else//如果相等,此节点就是要删除的节点 { if(node->lson&&node->rson)//此节点有两个儿子 { TreeNode<T>* temp=node->rson;//temp指向节点的右儿子 while(temp->lson!=NULL) temp=temp->lson;//找到右子树中值最小的节点 //把右子树中最小节点的值赋值给本节点 node->data=temp->data; node->freq=temp->freq; Deletepri(node->rson,temp->data);//删除右子树中最小值的节点 } else//此节点有1个或0个儿子 { TreeNode<T>* temp=node; if(node->lson==NULL)//有右儿子或者没有儿子 node=node->rson; else if(node->rson==NULL)//有左儿子 node=node->lson; delete(temp); } } return; } //删除接口 template<class T> void BST<T>::Delete(T x) { Deletepri(root,x); } //中序遍历函数 template<class T> void BST<T>::insubtree(TreeNode<T>* node) { if(node==NULL) return; insubtree(node->lson);//先遍历左子树 cout<<node->data<<" ";//输出根节点 insubtree(node->rson);//再遍历右子树 } //中序遍历接口 template<class T> void BST<T>::traversal() { insubtree(root); }
第一步:节点信息
二叉查找树的节点和二叉树的节点大部分是一样的,不同的是,二叉查找树多了一个值出现的次数。如图1显示了二叉查找树的节点信息。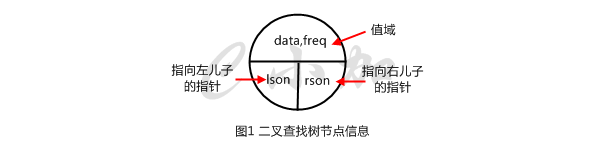
代码如下:
//二叉查找树节点信息 template<class T> class TreeNode { public: TreeNode():lson(NULL),rson(NULL),freq(1){}//初始化 T data;//值 unsigned int freq;//频率 TreeNode* lson;//指向左儿子的坐标 TreeNode* rson;//指向右儿子的坐标 };
第二步:二叉查找树类的声明
代码如下:
//二叉查找树类的属性和方法声明 template<class T> class BST { private: TreeNode<T>* root;//根节点 void insertpri(TreeNode<T>* &node,T x);//插入 TreeNode<T>* findpri(TreeNode<T>* node,T x);//查找 void insubtree(TreeNode<T>* node);//中序遍历 void Deletepri(TreeNode<T>* &node,T x);//删除 public: BST():root(NULL){} void insert(T x);//插入接口 TreeNode<T>* find(T x);//查找接口 void Delete(T x);//删除接口 void traversal();//遍历接口 };
第三步:插入
根据二叉查找树的性质,插入一个节点的时候,如果根节点为空,就此节点作为根节点,如果根节点不为空,就要先和根节点比较,如果比根节点的值小,就插入到根节点的左子树中,如果比根节点的值大就插入到根节点的右子树中,如此递归下去,找到插入的位置。重复节点的插入用值域中的freq标记。如图2是一个插入的过程。
二叉查找树的时间复杂度要看这棵树的形态,如果比较接近一一棵完全二叉树,那么时间复杂度在O(logn)左右,如果遇到如图3这样的二叉树的话,那么时间复杂度就会恢复到线性的O(n)了。
平衡二叉树会很好的解决如图3这种情况。
插入函数的代码如下:
//插入 template<class T> void BST<T>::insertpri(TreeNode<T>* &node,T x) { if(node==NULL)//如果节点为空,就在此节点处加入x信息 { node=new TreeNode<T>(); node->data=x; return; } if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中插入x { insertpri(node->lson,x); } else if(node->data<x)//如果x大于节点的值,就继续在节点的右子树中插入x { insertpri(node->rson,x); } else ++(node->freq);//如果相等,就把频率加1 } //插入接口 template<class T> void BST<T>::insert(T x) { insertpri(root,x); }
第四步:查找
查找的功能和插入差不多一样,按照插入那样的方式递归下去,如果找到了,就返回这个节点的地址,如果没有找到,就返回NULL。
代码如下:
//查找 template<class T> TreeNode<T>* BST<T>::findpri(TreeNode<T>* node,T x) { if(node==NULL)//如果节点为空说明没找到,返回NULL { return NULL; } if(node->data>x)//如果x小于节点的值,就继续在节点的左子树中查找x { return findpri(node->lson,x); } else if(node->data<x)//如果x大于节点的值,就继续在节点的左子树中查找x { return findpri(node->rson,x); } else return node;//如果相等,就找到了此节点 } //查找接口 template<class T> TreeNode<T>* BST<T>::find(T x) { return findpri(root,x); }
第五步:删除
删除会麻烦一点,如果是叶子节点的话,直接删除就可以了。如果只有一个孩子的话,就让它的父亲指向它的儿子,然后删除这个节点。图4显示了一棵初始树和4节点被删除后的结果。先用一个临时指针指向4节点,再让4节点的地址指向它的孩子,这个时候2节点的右儿子就变成了3节点,最后删除临时节点指向的空间,也就是4节点。
删除有两个儿子的节点会比较复杂一些。一般的删除策略是用其右子树最小的数据代替该节点的数据并递归的删除掉右子树中最小数据的节点。因为右子树中数据最小的节点肯定没有左儿子,所以删除的时候容易一些。图5显示了一棵初始树和2节点被删除后的结果。首先在2节点的右子树中找到最小的节点3,然后把3的数据赋值给2节点,这个时候2节点的数据变为3,然后的工作就是删除右子树中的3节点了,采用递归删除。
我们发现对2节点右子树的查找进行了两遍,第一遍找到最小节点并赋值,第二遍删除这个最小的节点,这样的效率并不是很高。你能不能写出只查找一次就可以实现赋值和删除两个功能的函数呢?
如果删除的次数不是很多的话,有一种删除的方法会比较快一点,名字叫懒惰删除法:当一个元素要被删除时,它仍留在树中,只是多了一个删除的标记。这种方法的优点是删除那一步的时间开销就可以避免了,如果重新插入删除的节点的话,插入时也避免了分配空间的时间开销。缺点是树的深度会增加,查找的时间复杂度会增加,插入的时间可能会增加。
删除函数代码如下:
//删除 template<class T> void BST<T>::Deletepri(TreeNode<T>* &node,T x) { if(node==NULL) return ;//没有找到值是x的节点 if(x < node->data) Deletepri(node->lson,x);//如果x小于节点的值,就继续在节点的左子树中删除x else if(x > node->data) Deletepri(node->rson,x);//如果x大于节点的值,就继续在节点的右子树中删除x else//如果相等,此节点就是要删除的节点 { if(node->lson&&node->rson)//此节点有两个儿子 { TreeNode<T>* temp=node->rson;//temp指向节点的右儿子 while(temp->lson!=NULL) temp=temp->lson;//找到右子树中值最小的节点 //把右子树中最小节点的值赋值给本节点 node->data=temp->data; node->freq=temp->freq; Deletepri(node->rson,temp->data);//删除右子树中最小值的节点 } else//此节点有1个或0个儿子 { TreeNode<T>* temp=node; if(node->lson==NULL)//有右儿子或者没有儿子 node=node->rson; else if(node->rson==NULL)//有左儿子 node=node->lson; delete(temp); } } return; } //删除接口 template<class T> void BST<T>::Delete(T x) { Deletepri(root,x); }
第六步:中序遍历
遍历的方法和二叉树的方法一样,写这个方法的目的呢,是输出这个二叉查找树的有序序列。
代码如下:
//中序遍历函数 template<class T> void BST<T>::insubtree(TreeNode<T>* node) { if(node==NULL) return; insubtree(node->lson);//先遍历左子树 cout<<node->data<<" ";//输出根节点 insubtree(node->rson);//再遍历右子树 } //中序遍历接口 template<class T> void BST<T>::traversal() { insubtree(root); }
到此,整个代码就完成了,代码中肯定有很多不完善的地方请指出,我会加以完善,谢谢。
对于二叉查找树不稳定的时间复杂度的解决方案有不少,平衡二叉树、伸展树和红黑树都可以解决这个问题,但效果是不一样的。
标签:
原文地址:http://www.cnblogs.com/wyj-jenny/p/5767550.html