标签:
T1
T2
T3 小奇回地球
【问题描述】
简单来说,它要从标号为1的星球到标号为n的星球,某一些星球之间有航线。由于超时空隧道的存在,从一个星球到另一个星球时间可能会倒流,而且,从星球a到b耗费的时间和星球b到a耗费的时间不一定相同。
宇宙法规定:“禁止在出发时间前到达目的地。”
每艘飞船上都有速度调节装置,可以调节飞行的时间。其功能可以使得整次航程中所有两星球间的飞行时间增加或减少相同的整数值。你的任务是帮助它调整速度调节器,找出一条最短时间到达目的地的路径。
【输入格式】
输入文件包含多组数据,第1个数为T,表示数据组数。
对于每组数据,输入第1行为两个正整数n,m,为星球的个数和星球间的路线数。接下来m行,每行三个整数i,j和t,表示由星球i到星球j飞行的时间为t。由i到j最多只会有一条飞行线路。
【输出格式】
输出文件共T行,每组数据输出一行。
如果可以通过调节速度调节器完成任务,则输出一个非负整数,表示由星球1到星球n的最短时间。(注意最短时间要大于或者等于0)。
如果不能由星球1到达星球n,则输出-1。
【样例输入】
1
4 5
1 2 1
1 3 1
2 3 -3
3 1 1
3 4 1
【样例输出】
2
【样例解释】
把速度控制器的值设为1,相当于每个时间值加1,得到的最短路径为1→2→3→4,所需时间为2+(-2)+2=2。
【数据范围】
1,2号测试点,保证所有星球出度不超过1
3,4号测试点,n<=10
5,6号测试点,-100<=t<=100
对于100%的数据T<=10,n<=100,m<=n*(n-1),-100000<=t<=100000
数据随机和构造结合生成
这题的题意好含糊。。理解错了好多次。。理解错了就不会做了(迷之微笑)
题意:给定一个有向图,每条边有一个权值,可以给所有边加或减同一个值k(k为整数),使得1到n的最短路存在,最短路>=0且尽量小。
正确理解:
如果1到n的路径中有负环,那最短路就不存在;
如果1到n的最短路是负数,那也不满足题意。
题解:
我们可以发现k具有单调性:如果+k都还存在负环or最短路为负,那比k小的更加不满足题意;反之,比k大的必定满足题意。
二分k,spfa判断图中是否有负环、并求出最短路,判断是否满足题意。
注意:判断负环前应删去那些与起点、终点不是都联通的点!
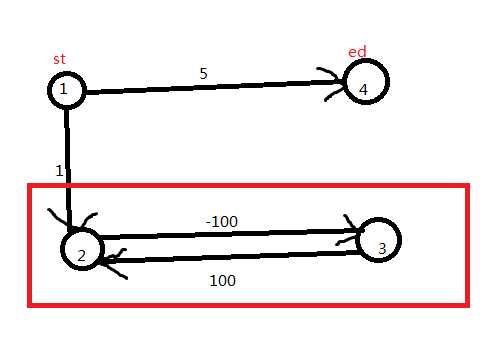
比如这种情况,图中存在负环,但是与1到n的最短路无关,错误输出为105,正确输出为5。
优化:用spfa判断负环的方法
判断给定的有向图中是否存在负环。
利用 spfa 算法判断负环有两种方法:
1) spfa 的 dfs 形式,判断条件是存在一点在一条路径上出现多次。
2) spfa 的 bfs 形式,判断条件是存在一点入队次数大于总顶点数。
SPFA的两种写法,bfs和dfs,bfs判别负环不稳定,相当于限深度搜索,但是设置得好的话还是没问题的,dfs的话判断负环很快。
我原本的方法是在bfs里加一个数组,记录每个点入队了多少次,如果有一个点入队次数大于n则有负环。
时间是这样的:
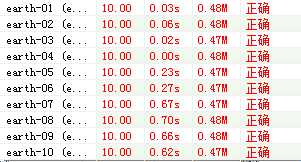
改成dfs:
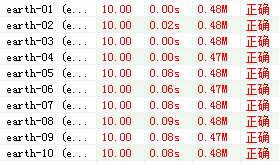
改成dfs这里调了挺久的。但是的确快了很多。
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<queue> 6 using namespace std; 7 8 const int N=110,Inf=(int)1e9; 9 struct node{ 10 int x,y,d,next; 11 }a[N*N]; 12 int n,m,len,dis[N],first[N]; 13 bool in[N],can[N],vis[N]; 14 queue<int> q; 15 16 int read() 17 { 18 int x=0,f=1;char ch=getchar(); 19 while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} 20 while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} 21 return x*f; 22 } 23 24 void ins(int x,int y,int d) 25 { 26 len++; 27 a[len].x=x;a[len].y=y;a[len].d=d; 28 a[len].next=first[x];first[x]=len; 29 } 30 31 int minn(int x,int y){return x<y ? x:y;} 32 33 void dfs(int x) 34 { 35 vis[x]=1; 36 for(int i=first[x];i;i=a[i].next) 37 if(!vis[a[i].y]) dfs(a[i].y); 38 } 39 40 bool dfs_spfa(int x,int ad) 41 { 42 in[x]=1; 43 for(int i=first[x];i;i=a[i].next) 44 { 45 int y=a[i].y; 46 if(dis[y]>dis[x]+a[i].d+ad && can[y]) 47 { 48 if(in[y]) return 1;//负边成环 49 dis[y]=dis[x]+a[i].d+ad;//虽然dis[x]=dis[y]=0,但如果是负边,a[i].d+ad<0 50 if(dfs_spfa(y,ad)) return 1; 51 } 52 } 53 in[x]=0; 54 return 0; 55 } 56 57 void bfs_spfa(int ad) 58 { 59 while(!q.empty()) q.pop(); 60 memset(dis,63,sizeof(dis)); 61 memset(in,0,sizeof(in)); 62 q.push(1);dis[1]=0;in[1]=1; 63 while(!q.empty()) 64 { 65 int x=q.front();in[x]=0;q.pop(); 66 for(int i=first[x];i;i=a[i].next) 67 { 68 int y=a[i].y; 69 int d=a[i].d+ad; 70 if(dis[y]>dis[x]+d && can[y]) 71 { 72 dis[y]=dis[x]+d; 73 if(!in[y]) in[y]=1,q.push(y); 74 } 75 } 76 } 77 } 78 79 bool judge(int ad) 80 { 81 // 判断是否有负环 82 for(int i=1;i<=n;i++) 83 if(can[i]) 84 { 85 memset(dis,0,sizeof(dis));//不用算具体数值,只要求到有负环即可。 86 memset(in,0,sizeof(in)); 87 if(dfs_spfa(i,ad)) return 0;//dfs_spfa(i)相当于找i这个点是不是在一个负环中,所以要每个点都做一遍,不是在负环中很快就会跳出,否则就遍历一遍负环。 88 } 89 //屏蔽了的这种方法理论上也可以,但是相当于用dfs做了一遍spfa,比bfs更慢,超时。 90 /* memset(dis,63,sizeof(dis));dis[1]=0; 91 memset(in,0,sizeof(in)); 92 if(can[1]==0) return 0; 93 if(can[1]==1 && dfs_spfa(1,ad)) return 0;*/ 94 //跑最短路 95 bfs_spfa(ad); 96 if(dis[n]>=0 && dis[n]<=Inf) return 1; 97 return 0; 98 } 99 100 int main() 101 { 102 // freopen("a.in","r",stdin); 103 freopen("earth.in","r",stdin); 104 freopen("earth.out","w",stdout); 105 int T; 106 scanf("%d",&T); 107 while(T--) 108 { 109 len=0; 110 memset(first,0,sizeof(first)); 111 n=read(),m=read(); 112 int mn=0; 113 for(int i=1;i<=m;i++) 114 { 115 int x=read(),y=read(),d=read(); 116 ins(x,y,d); 117 } 118 memset(vis,0,sizeof(vis)); 119 dfs(1); 120 for(int i=1;i<=n;i++) 121 { 122 if(vis[i]) can[i]=1; 123 else can[i]=0; 124 //can[x]=1 x点与起点联通 125 } 126 for(int i=1;i<=n;i++) 127 { 128 if(can[i]) 129 { 130 memset(vis,0,sizeof(vis)); 131 dfs(i); 132 if(!vis[n]) can[i]=0; 133 } 134 }//can[x]=1 x点与起点、终点都联通 135 int l=-100000,r=100000,ans=-1; 136 while(l<=r)//二分加或减多少 137 { 138 int mid=(l+r)>>1; 139 if(judge(mid)) ans=dis[n],r=mid-1; 140 else l=mid+1; 141 // printf("l = %d r = %d\n",l,r); 142 } 143 printf("%d\n",ans); 144 } 145 return 0; 146 }
标签:
原文地址:http://www.cnblogs.com/KonjakJuruo/p/5771160.html