机器学习读后感-0

    开篇先说工作范式，工作范式是解决某类问题采用的基本框架。通常在遇到一类特定问题时我们会自动在已知的方法中找出一个，然后按步骤把问题一步步分解下去，最终达到解决问题的目的。范式就是具体按步骤分解，求解的过程。最常见的就是工作流程，不同的单位财务流程不同，就说他们在财务问题上使用不同的范式。点到为止，下面就来看点具体的。

 

    在40年代之前，代数公式是解决现实问题的主要工具。代数公式同时还是描述研究对象本身的工具。通常我们会这么干，研究一个物体的匀速运动时。先写下一段描述文字.定义速度为s,定义时间为t,具体位置为d，起始位置为f. 找个中学身看一下牛顿的文章，随后如下公式：d=s*t+f. 到此，一切顺利。下面找来一组实际测试的数据，放进去算一通，结果符合实测情况,顿时很满意。但如果提出进一步的要求：请按照公式造一个设备，能满足这个公式。这时大学生就懵逼了，这怎么造没人教过。不过有的是牛人，把达芬奇叫过来，叮咚一通乱敲后，给你一个带刻度的匀速齿轮。问题解决了！此时第一个问题出来了：从公式到设备设计之间没有范式可用。

 

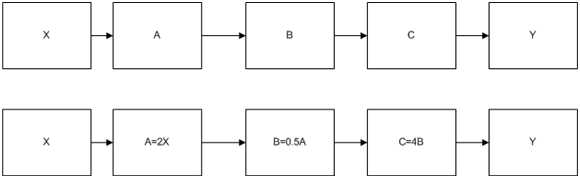
    再往下，如果研究对象进一步复杂，给你一块机械手表。要求你对里面每个齿轮的转速的速度写个公式描述它，以便随时了解里面的运转情况。顿时就觉得头有些晕。Cybernetic在40年代引入一个叫系统框图的东西，后来被普遍使用。具体说来就是把相关的齿轮依次用A/B/C形式画出来。然后只要耐心研究上一齿轮和下一齿轮之间的关系就能把整个图画下来.最后按照关系把代数公式写出来。最终用点合并同类项之类的方法简化一下，就直接可以算X/Y的关系。到这里，就获得了一种从形式到建模之间的基本方法。同时它也提供了一种可以从公式到设备设计之间的方法，有公式的框图只需要找到对应功能的零件就可以设计符合代数公式的设备，两张图完全可以反推。这就是工作范式来的差异。

 

    

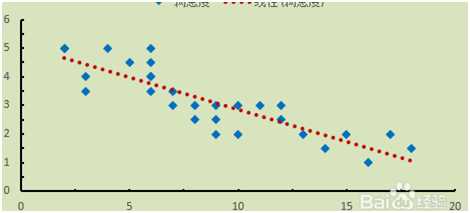
 再来，换个思路，如果我们知道某个具体的一些输入和输出样本，也就是知道一些x,Y的具体内容。如何获知函数的表达形式？数学上给了提供了大家都知道的基本的方法-拟合(名字很牛掰，英文叫做fitting,其实就是适配)。而具体的方法最典型的就是线性回归(Linear Regression名字也很牛掰，其实这名字就是回到从前的意思 )。

 

这套方法暴力的解读就是猜，因为以前的的数据都能基本符合这个猜出来的公式，所以能假定其他未知的数据也能符合这个规律。因为是猜，所以就有猜得好不好的问题，所以要评估猜的质量，所以书里面教我们用类似方差这些评估方法来衡量猜测的好坏。对于一个特定的数据而然，数学的通行逻辑显然不如人自己的判断，如果看到一组符合抛物线的数据，我们会很自然的把数据拟合到这条我们已知规律的曲线上，而不是简单的按照死板的直线拟合。对新的数据完全可以按照新的曲线规律进行推测。以得到更好的结果。但能不能找到一个公式直接让我们找到那条更好的曲线呢，这里我们保留这个问题。