标签:

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 using namespace std; 7 typedef long long int64; 8 const int mod=1000000007; 9 #define maxn 2000005 10 int top,tot,d[maxn],prim[maxn],mu[maxn]; 11 bool vis[maxn]; 12 int64 n,f[maxn],ans; 13 void prepare(){ 14 tot=top=0,memset(vis,1,sizeof(vis)),mu[0]=0,mu[1]=1,f[1]=1; 15 for (int i=2;i<maxn;i++){ 16 if (vis[i]==1){ 17 prim[++top]=i; 18 d[i]=i; 19 mu[i]=-1; 20 f[i]=2; 21 } 22 for (int j=1;j<=top;j++){ 23 if (i*prim[j]>=maxn) break; 24 vis[i*prim[j]]=0; 25 if (i%prim[j]==0){ 26 d[i*prim[j]]=d[i]*prim[j]; 27 mu[i*prim[j]]=0; 28 f[i*prim[j]]=f[i/d[i]]*(f[d[i]]+1); 29 break; 30 }else{ 31 d[i*prim[j]]=prim[j]; 32 mu[i*prim[j]]=mu[i]*mu[prim[j]]; 33 f[i*prim[j]]=f[i]*f[prim[j]]; 34 } 35 } 36 } 37 for (int i=2;i<maxn;i++) mu[i]+=mu[i-1]; 38 for (int i=2;i<maxn;i++) f[i]=(f[i-1]+f[i])%mod; 39 } 40 #define maxp 100007 41 #define maxm 4000005 42 int now[maxp],prep[maxm]; 43 int64 val[maxm],id[maxm]; 44 void insert(int x,int64 y){ 45 int pos=x%maxp; 46 prep[++tot]=now[pos],now[pos]=tot,val[tot]=y,id[tot]=x; 47 } 48 int64 find(int x){ 49 int pos=x%maxp; 50 for (int i=now[pos];i;i=prep[i]){ 51 if (id[i]==x) return val[i]; 52 } 53 return -1; 54 } 55 int64 Mu(int x){ 56 if (x<maxn) return mu[x]; 57 int64 temp=find(x),t; 58 if (temp!=-1) return temp; 59 temp=1; 60 for (int j,i=2;i<=x;i=j+1){ 61 j=x/(x/i); t=Mu(x/i); 62 temp=((temp-1LL*(j-i+1)*t%mod)%mod+mod)%mod; 63 } 64 insert(x,temp); return temp; 65 } 66 int64 F(int x){ 67 if (x<maxn) return f[x]; 68 int64 temp=0; 69 for (int j,i=1;i<=x;i=j+1){ 70 j=x/(x/i); 71 temp=(temp+1LL*(x/i)*(j-i+1)%mod)%mod; 72 } 73 return temp%mod; 74 } 75 int main(){ 76 int64 temp; 77 prepare(); 78 scanf("%lld",&n); 79 ans=0; 80 for (int j,i=1;i<=n;i=j+1){ 81 j=n/(n/i); temp=F(n/i); 82 ans=(ans+1LL*(Mu(j)-Mu(i-1))%mod*temp%mod*temp%mod)%mod; 83 } 84 printf("%lld\n",(ans%mod+mod)%mod); 85 return 0; 86 }
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=4176
题目大意:
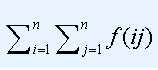 答案对10^9+7取模。 1<=n<=10^9,单组询问。
答案对10^9+7取模。 1<=n<=10^9,单组询问。
吐槽:这是一个对我来说启发很大的题,加深了我对杜教筛的理解。
做法:式子不好写,还是用图好了。

然后用莫比乌斯反演继续化简:
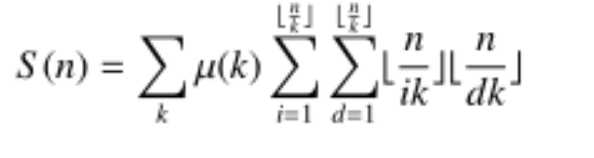

这样就好办了,floor(n/k)最多只有O(sqrt(n))级别的取值,维护mu的前缀和?没错,既然不能预处理,那我们就杜教筛,F数组呢,没错,F[i]=sigam(i/j),1<=j<=i,可以sqrt(n)级别的复杂度做出,如果我们尽可能多的预处理出mu和F,那么可以把总复杂度降至O(n^(2/3)),足以过此题。
标签:
原文地址:http://www.cnblogs.com/OYzx/p/5778390.html