标签:
转载自:http://www.cnblogs.com/hxsyl/archive/2012/10/10/2718380.html
转载自:http://www.cnblogs.com/jeromeblog/p/3396494.html
plot选项:
一 基础功能
二维图形
一、 plot函数
① 函数格式:plot(x,y) 其中x和y为长度相同
坐标向量
函数功能:以向量x、y为轴,绘制曲线。
【例】 在区间0≤X≤2?内,绘制正弦曲线y=sin(x)
其程序为:
x=0:pi/100:2*pi; %必须加上分号,否则x直接显示出来啦
y=sin(x); %必须加上分号,否则x直接显示出来啦
plot(x,y)
【例】在0≤x≤2?区间内,绘制曲线 y=2e-0.5xcos(4πx)
程序如下:
x=0:pi/100:2*pi;
y=2*exp(-0.5*x).*cos(4*pi*x);
plot(x,y)
plot函数最简单的调用格式是只包含一个输入参数:
plot(x)
在这种情况下,当x是实向量时,以该向量元素的下标为横坐标,元素值为纵坐标画出一条连续曲线,这实际上是绘制折线图。
② 含多个输入参数的plot函数调用格式为: plot(x1,y1,x2,y2,…,xn,yn)
Ⅰ.当输入参数都为向量时,x1和y1,x2和y2,…,xn和yn分别组成一组向量对,每一组向量对的长度可以不同。每一向量对可以绘制出一条曲线,这样可以在同一坐标内绘制出多条曲线。
Ⅱ.当输入参数有矩阵形式时,配对的x,y按对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
【例】同时绘制正、余弦两条曲线y1=sin(x)和
y2=cos(x),其程序为:
x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2)
或者
x=[0:0.5:360]*pi/180;
plot(x,sin(x),x,cos(x))
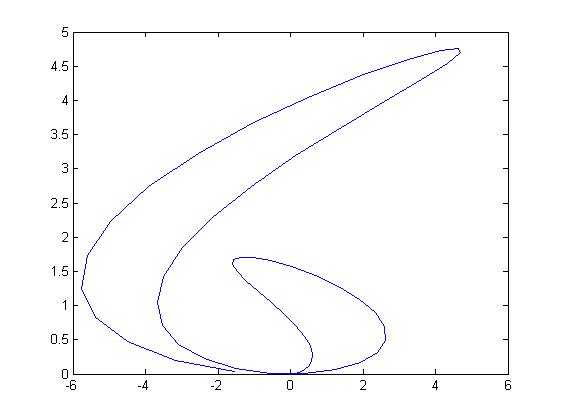
中间变量绘图
t=0:0.1:2*pi;
x=t.*sin(3*t); %.*表示点乘,*表示矩阵乘法
y=t.*sin(t).*sin(t);
plot(x,y);
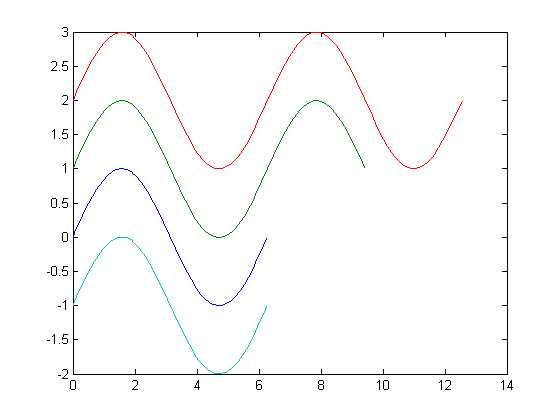
【例】 分析下列程序绘制的曲线。
x1=linspace(0,2*pi,100);
x2=linspace(0,3*pi,100);
x3=linspace(0,4*pi,100);
y1=sin(x1);
y2=1+sin(x2);
y3=2+sin(x3);
x=[x1;x2;x3]‘;
y=[y1;y2;y3]‘;
plot(x,y,x1,y1-1)
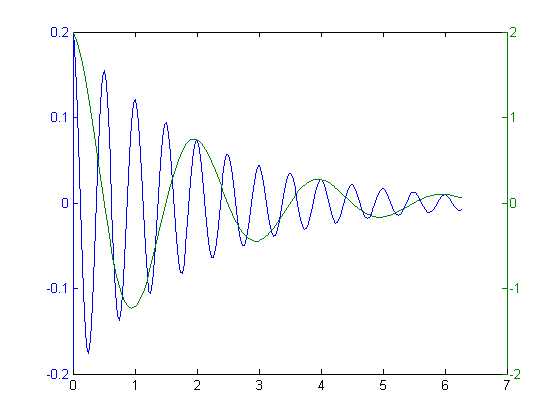
③ 具有两个纵坐标标度的图形
在MATLAB中,如果需要绘制出具有不同纵坐标标度的两个图形,可以使用plotyy绘图函数。调用格式为:
plotyy(x1,y1,x2,y2)
其中x1,y1对应一条曲线,x2,y2对应另一条曲线。横坐标的标度相同,纵坐标有两个,左纵坐标用于x1,y1数据对,右纵坐标用于x2,y2数据对。
【例】用不同标度在同一坐标内绘制曲线
y1=0.2e-0.5xcos(4πx) 和
y2=2e - 0.5xcos(πx)
④ 图形保持
hold on/off命令控制是保持原有图形还是刷新原有图形,不带参数的hold命令在两种状态之间进行切换。
hold on:启动图形保持功能,当前坐标轴和图形都将保持,此后绘制的图形都将添加在这个图形之上,并且自动调整坐标轴的范围。
hold off:关闭图形保持功能。
hold :在hold on 和hold off命令之间进行切换。
【例】采用图形保持,在同一坐标内绘制曲线y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx)。
程序如下:
x=0:pi/100:2*pi;
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
plot(x,y1)
hold on
y2=2*exp(-0.5*x).*cos(pi*x);
plot(x,y2);
hold off
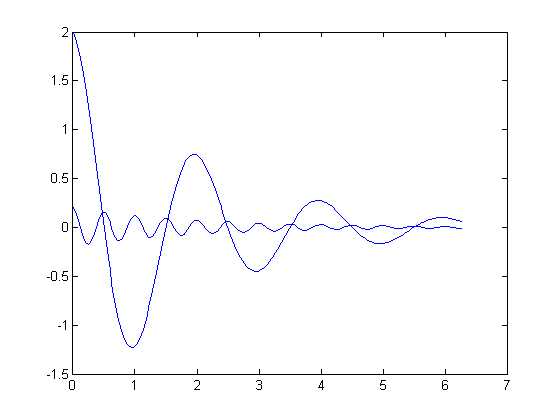
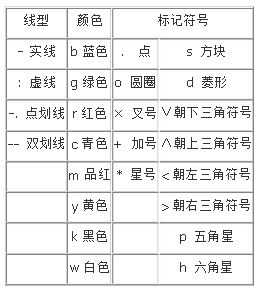
二、设置曲线样式格式:
MATLAB提供了一些绘图选项,用于确定所绘曲线的线型、颜色和数据点标记符号,它们可以组合使用。例如,“b-.”表示蓝色点划线,“y:d”表示黄色虚线并用菱形符标记数据点。当选项省略时,MATLAB规定,线型一律用实线,颜色将根据曲线的先后顺序依次。
调用格式为:plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n)
要设置曲线样式可以在plot函数中加绘图选项,其调用格式为:
plot(x,y1,’cs’,...)
其中c表示颜色, s表示线型。
【例】 用不同线型和颜色重新绘制例2图形,其程序为:
x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,‘go‘,x,y2,‘b-.‘)
其中参数‘go‘和‘b-.‘表示图形的颜色和线型。g表示绿色,o表示图形线型为圆圈;b表示蓝色,-.表示图形线型为点划线。
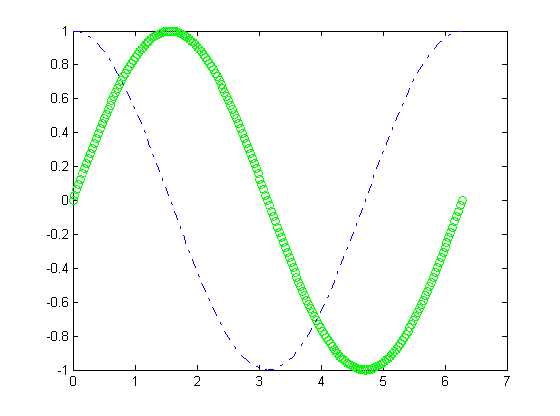
【例】在同一坐标内,分别用不同线型和颜色绘制曲线y1=0.2e-0.5xcos(4πx) 和y2=2e-0.5xcos(πx),标记两曲线交叉点。
x=linspace(0,2*pi,1000);
y1=0.2*exp(-0.5*x).*cos(4*pi*x);
y2=2*exp(-0.5*x).*cos(pi*x);
k=find(abs(y1-y2)<1e-2);
%查找y1与y2相等点(近似相等)的下标
x1=x(k); %取y1与y2相等点的x坐标
y3=0.2*exp(-0.5*x1).*cos(4*pi*x1);
%求y1与y2值相等点的y坐标
plot(x,y1,x,y2,‘k:‘,x1,y3,‘bp‘);
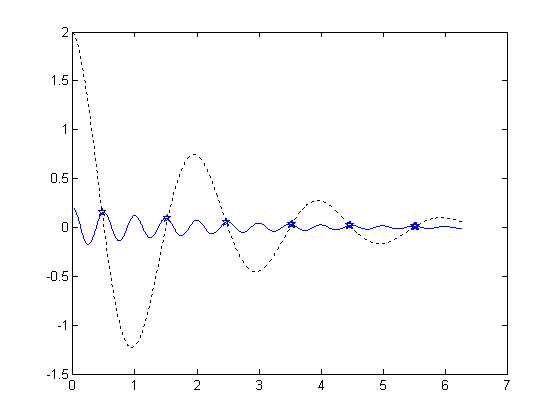
三、图形标记
在绘制图形的同时,可以对图形加上一些说明,如图形名称、图形某一部分的含义、坐标说明等,将这些操作称为添加图形标记。
title(‘加图形标题’);当前轴的正上方居
中位置处输出文本作为标题
xlabel(‘加X轴标记‘);
ylabel(‘加Y轴标记‘);
text(X,Y,‘添加文本‘);
函数中的说明文字,除使用标准的ASCII字符外,还可使用LaTeX格式的控制字符,这样就可以在图形上添加希腊字母、数学符号及公式等内容。例如,text(0.3,0.5,‘sin({\omega}t+{\beta})’)将得到标注效果sin(ωt+β)。
x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,‘b*‘,x,y2,‘r>‘);
title(‘绘制正弦,余弦函数‘);
% title(date);
xlabel(‘横轴‘);
ylabel(‘纵轴‘);
text(2,1,‘正弦曲线‘);
text(1,0.6,‘余弦曲线‘);
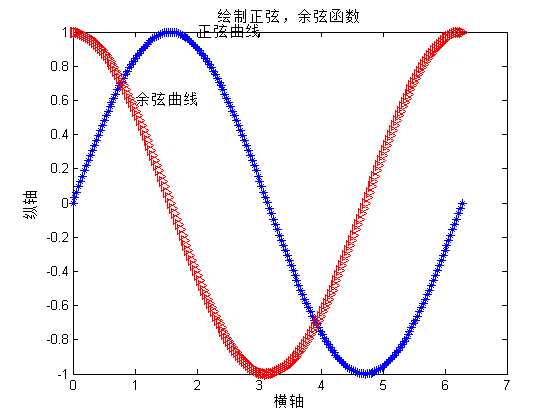
【例】 在坐标范围0≤X≤2π,-2≤Y≤2内重新绘制正弦曲线,其程序为:
x=linspace(0,2*pi,60);
%生成含有60个数据元素的向量X
y=sin(x);
plot(x,y);
axis ([0 2*pi -2 2]);

四、坐标控制
axis函数的调用格式为:
axis([xmin xmax ymin ymax zmin zmax])
axis函数功能丰富,常用的格式还有:
axis equal:纵、横坐标轴采用等长刻度。
axis square:产生正方形坐标系(缺省为矩形)。
axis auto:使用缺省设置。
axis off:取消坐标轴。
axis on:显示坐标轴。
给坐标加网格线用grid命令来控制。grid on/off命令控制是画还是不画网格线,不带参数的grid命令在两种状态之间进行切换。
给坐标加边框用box命令来控制。box on/off命令控制是加还是不加边框线,不带参数的box命令在两种状态之间进行切换。
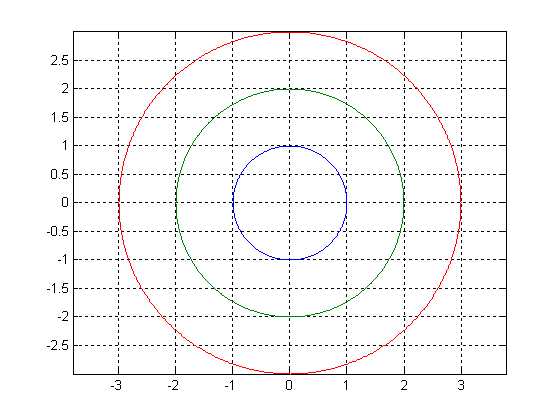
五、加图例
给图形加图例命令为legend。该命令把图例放置在图形空白处,用户还可以通过鼠标移动图例,将其放到希望的位置。
格式:legend(‘图例说明‘,‘图例说明‘);
【例】 为正弦、余弦曲线增加图例,其程序为:
x=0:pi/100:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2, ‘--‘);
legend(‘sin(x)‘,‘cos(x)‘);
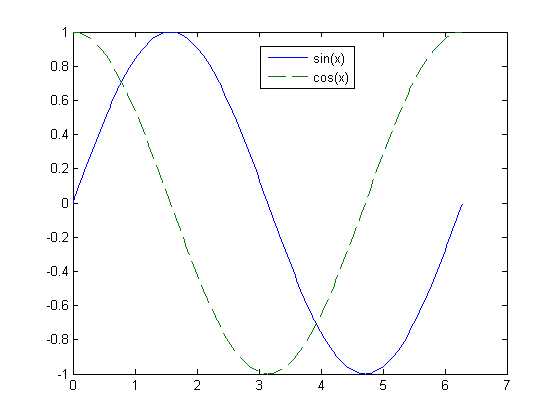
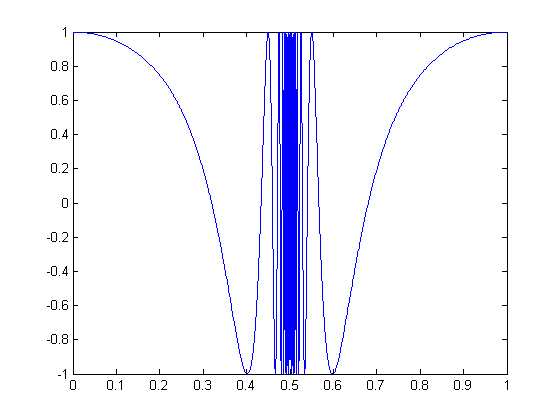
六、对函数自适应采样的绘图函数
fplot函数则可自适应地对函数进行采样,能更好地反应函数的变化规律。
fplot函数的调用格式为:
fplot(fname,lims,tol,选项)
其中fname为函数名,以字符串形式出现,lims为x,y的取值范围,tol为相对允许误差,其系统默认值为2e-3。选项定义与plot函数相同。
【例】用fplot函数绘制f(x)=cos(tan(πx))的曲线。
命令如下:
fplot(‘cos(tan(pi*x))‘,[ 0,1],1e-4)
或可先建立函数文件fct.m,其内容为:
function y=fct(x)
y=cos(tan(pi*x));
用fplot函数调用fct.m函数,其命令为:
fplot(‘fct’,[0 1])
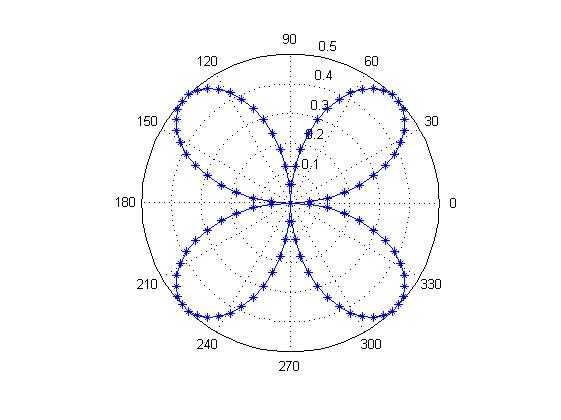
七.极坐标图
polar函数用来绘制极坐标图,其调用格式为:
polar(theta,rho,选项)
其中theta为极坐标极角,rho为极坐标矢径,选项的内容与plot函数相似。
例 绘制r=sin(t)cos(t)的极坐标图,并标记数据点。
程序如下:
1 t=0:pi/50:2*pi; 2 r=sin(t).*cos(t); 3 polar(t,r,‘-*‘);
八. 图形标记
title(‘加图形标题‘);
xlabel(‘加X轴标记‘);
ylabel(‘加Y轴标记‘);
text(X,Y,‘添加文本‘);
Legend(‘sin(x)’);%加图例
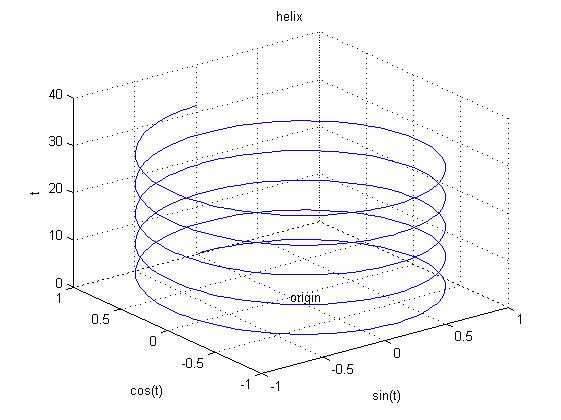
绘制三维螺旋曲线
1 t=0:pi/50:10*pi; 2 x=sin(t),y=cos(t); 3 plot3(x,y,t); 4 title(‘helix‘),text(0,0,0,‘origin‘); 5 xlabel(‘sin(t)‘),ylabel(‘cos(t)‘),zlabel(‘t‘); 6 grid on;%加上虚线网格线可以更好的看到对应区间的值
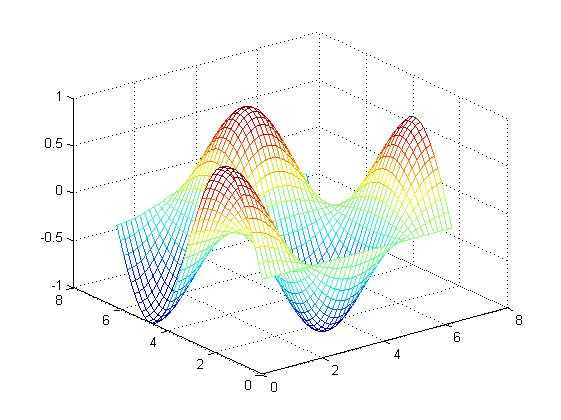
九.绘制三维网格图。函数格式:mesh(x,y,z,c)
其中:x,y控制X和Y轴坐标
矩阵z是由(x,y)求得Z轴坐标
(x,y,z)组成三维空间的网格点
c用于控制网格点颜色
1 %绘制三维网格曲面图 2 x=[0:0.15:2*pi]; 3 y=[0:0.15:2*pi]; 4 z=sin(y‘)*cos(x); %矩阵相乘 5 mesh(x,y,z);
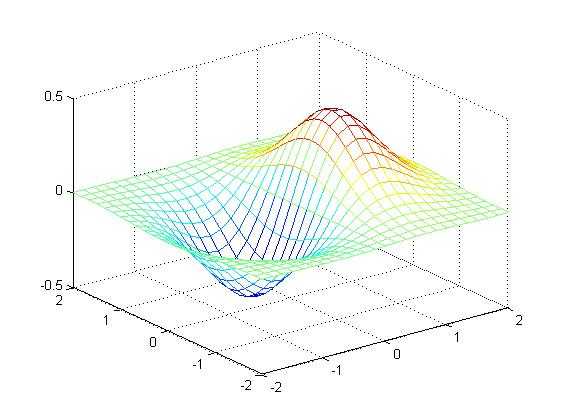
1 %画出由函数形成的立体网状图: 2 x=linspace(-2, 2, 25); % 在x轴上取25点 3 y=linspace(-2, 2, 25); % 在y轴上取25点 4 [xx,yy]=meshgrid(x,y); % xx和yy都是21x21的矩阵 5 zz=xx.*exp(-xx.^2-yy.^2); % 计算函数值,zz也是21x21的矩阵 6 mesh(xx, yy, zz); % 画出立体网状图
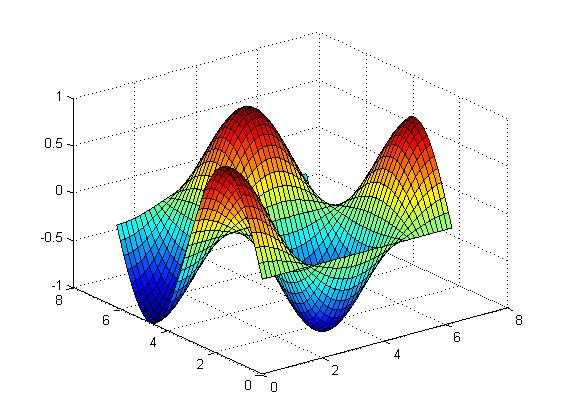
十.surf函数
绘制三维曲面图,各线条之间的补面用颜色填充。surf函数和mesh函数的调用格式一致。
函数格式: surf (x,y,z)
其中x,y控制X和Y轴坐标,矩阵z是由x,y求得的曲面上Z轴坐标。
1 % 绘制三维曲面图 2 x=[0:0.15:2*pi]; 3 y=[0:0.15:2*pi]; 4 z=sin(y‘)*cos(x); %矩阵相乘 5 surf(x,y,z);
1 %剔透玲珑球 2 [X0,Y0,Z0]=sphere(30); %产生单位球面的三维坐标 3 X=2*X0;Y=2*Y0;Z=2*Z0; %产生半径为2的球面的三维坐标,若加上常数则是圆心 4 surf(X0,Y0,Z0); %画单位球面 5 shading interp %采用插补明暗处理 6 hold on; mesh(X,Y,Z);hold off %画外球面 7 hidden off %产生透视效果 8 axis off %不显示坐标轴
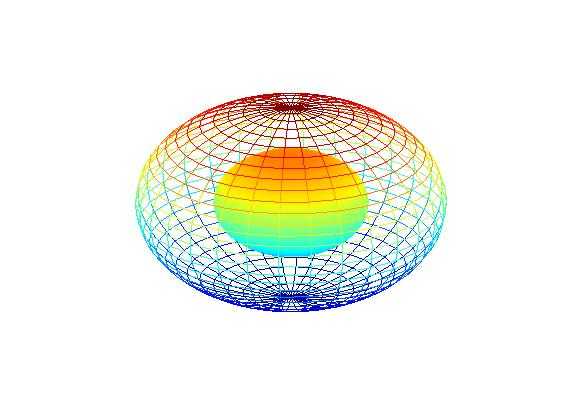
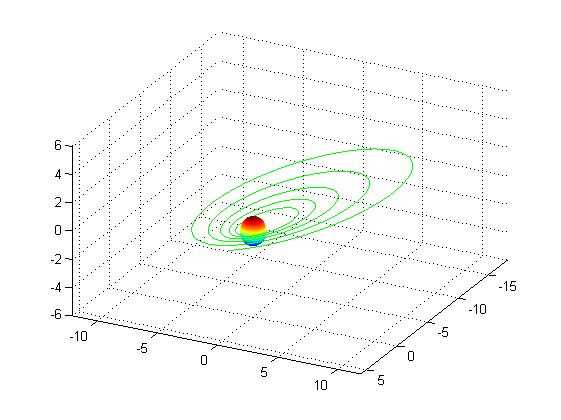
1 %卫星返回地球的运动轨线示意。 2 R0=1; %以地球半径为一个单位 3 a=12*R0;b=9*R0;T0=2*pi; %T0是轨道周期 4 T=5*T0;dt=pi/100;t=[0:dt:T]‘;f=sqrt(a^2-b^2); %地球与另一焦点的距离 5 th=12.5*pi/180; %卫星轨道与x-y平面的倾角 6 E=exp(-t/20); %轨道收缩率 7 x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t)); 8 plot3(x,y,z,‘g‘) %画全程轨线 9 [X,Y,Z]=sphere(30);X=R0*X;Y=R0*Y;Z=R0*Z; %获得单位球坐标 10 grid on,hold on,surf(X,Y,Z),shading interp %画地球 11 x1=-18*R0;x2=6*R0;y1=-12*R0;y2=12*R0;z1=-6*R0;z2=6*R0; 12 axis([x1 x2 y1 y2 z1 z2]) %确定坐标范围 13 view([117 37]),comet3(x,y,z,0.02),hold off %设视角、画运动轨线
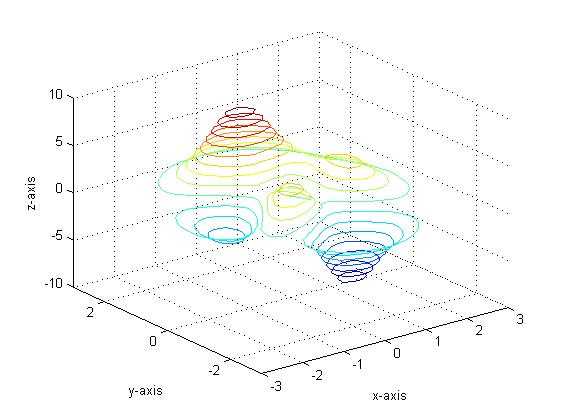
十一.等高线图
1 %多峰函数peaks的等高线图 2 [x,y,z]=peaks(30);%产生一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点 3 contour3(x,y,z,16); 4 xlabel(‘x-axis‘),ylabel(‘y-axis‘),zlabel(‘z-axis‘); 5 title(‘contour3 of peaks‘)
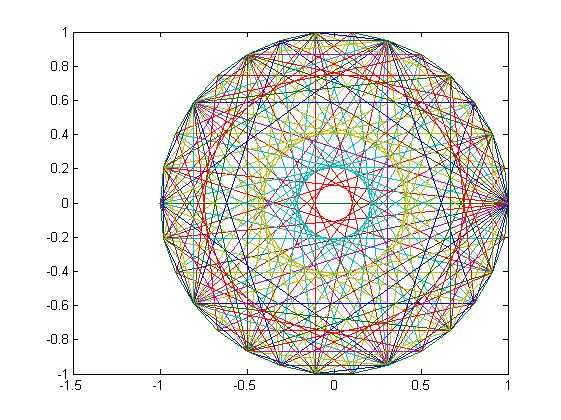
十二.动画设计
1 %动画功能函数:getframe、moviein和movie 2 %播放一个不断变化的眼球程序。 3 m=moviein(20); %建立一个20个列向量组成的矩阵 4 for j=1:20 5 plot(fft(eye(j+10))) %绘制出每一幅眼球图并保存到m矩阵中 6 m(:,j)=getframe; 7 end 8 movie(m,10);%以每秒10幅的速度播放画面
二 高级功能
图形是呈现数据的一种直观方式,在用Matlab进行数据处理和计算后,我们一般都会以图形的形式将结果呈现出来。尤其在论文的撰写中,优雅的图形无疑会为文章加分。本篇文章非完全原创,我的工作就是把见到的Matlab绘图代码收集起来重新跑一遍,修改局部错误,然后将所有的图贴上来供大家参考。大家可以先看图,有看中的可以直接把代码Copy过去改成自己想要的。
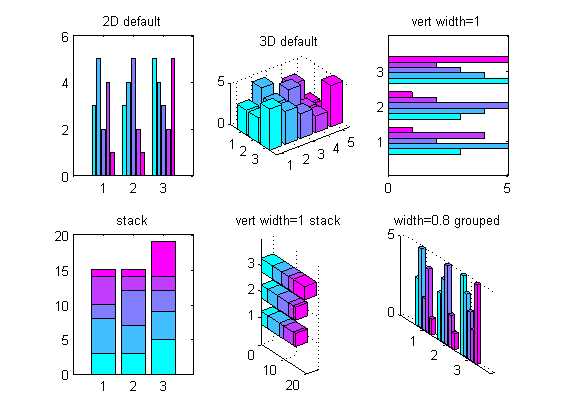
<br>%% 直方图图的绘制 %直方图有两种图型:垂直直方图和水平直方图。而每种图型又有两种表现模式:累计式:分组式。 figure; z=[3,5,2,4,1;3,4,5,2,1;5,4,3,2,5]; % 各因素的相对贡献份额 colormap(cool);% 控制图的用色 subplot(2,3,1); bar(z);%二维分组式直方图,默认的为‘group‘ title(‘2D default‘); subplot(2,3,2); bar3(z);%三维的分组式直方图 title(‘3D default‘); subplot(2,3,3); barh(z,1);%分组式水平直方图,宽度设置为1 title(‘vert width=1‘); subplot(2,3,4); bar(z,‘stack‘);%累计式直方图,例如:1,1+2,1+2+3构成了第一个bar title(‘stack‘) subplot(2,3,5); bar3h(z,0.5,‘stacked‘);%三维累计式水平直方图 title(‘vert width=1 stack‘); subplot(2,3,6); bar3(z,0.8,‘grouped‘);%对相关数据的颜色进行分组,默认的位‘group‘ title(‘width=0.8 grouped‘);
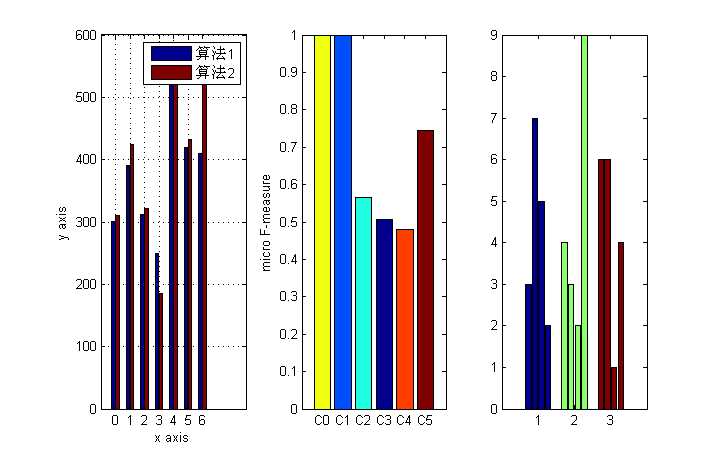
%% =========柱状图的进阶========== figure; y=[300 311;390 425; 312 321; 250 185; 550 535; 420 432; 410 520;]; subplot(1,3,1); b=bar(y); grid on; set(gca,‘XTickLabel‘,{‘0‘,‘1‘,‘2‘,‘3‘,‘4‘,‘5‘,‘6‘}) legend(‘算法1‘,‘算法2‘); xlabel(‘x axis‘); ylabel(‘y axis‘); %使仅有的一组柱状图呈现不同颜色,默认的位相同颜色 data = [1.0, 1.0, 0.565, 0.508, 0.481, 0.745]; subplot(1,3,2); b = bar(data); ch = get(b,‘children‘); set(ch,‘FaceVertexCData‘,[4;2;3;1;5;6]);%使用Indexed形式指定每组bar的颜色 set(gca,‘XTickLabel‘,{‘C0‘,‘C1‘,‘C2‘,‘C3‘,‘C4‘,‘C5‘}) axis([0 7 0.0 1.0]); ylabel(‘micro F-measure‘); %使每个bar颜色不同,默认的是每个元素在不同组的颜色相同 data = [3, 7, 5, 2;4, 3, 2, 9;6, 6, 1, 4]; subplot(1,3,3); b = bar(data); ch = get(b,‘children‘); set(ch{1},‘FaceVertexCData‘,[1;2;3]);%设置第一个元素在不同组的颜色 set(ch{2},‘FaceVertexCData‘,[1;2;3]);%设置第二个元素在不同组的颜色 set(ch{3},‘FaceVertexCData‘,[1;2;3]); set(ch{4},‘FaceVertexCData‘,[1;2;3]);
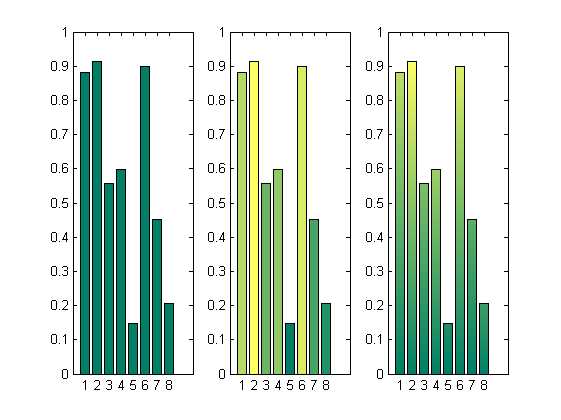
%% 彩色柱状图 %用到的数据 n = 8; Z = rand(n,1); figure; %默认图片 subplot(1,3,1); bar(Z); %简单的作图 % 这个图根据数据列中值的大小着色。每列中的值越大,颜色越突出 subplot(1,3,2); h=bar(Z); colormap(summer(n)); ch = get(h,‘Children‘); fvd = get(ch,‘Faces‘);%针对矩阵时,只能用fvd=get(ch{col},‘Faces‘),下同 fvcd = get(ch,‘FaceVertexCData‘); [~, izs] = sortrows(Z,1); for i = 1:n row = izs(i); fvcd(fvd(row,:)) = i; end set(ch,‘FaceVertexCData‘,fvcd) %图片会以渐变的方式着色,效果非常不错 subplot(1,3,3); h=bar(Z); ch = get(h,‘Children‘); fvd = get(ch,‘Faces‘); fvcd = get(ch,‘FaceVertexCData‘); [zs, izs] = sortrows(Z,1); k = 128; % 准备生成128 *3 行的colormap colormap(summer(k)); % 这样会产生一个128 * 3的矩阵,分别代表[R G B]的值 % 检视数据 whos ch fvd fvcd zs izs % Name Size Bytes Class Attributes % % ch 1x1 8 double % fvcd 66x1 528 double % fvd 13x4 416 double % izs 13x1 104 double % zs 13x1 104 double % shading interp % Needed to graduate colors for i = 1:n color = floor(k*i/n); % 这里用取整函数获得color在colormap中行 row = izs(i); % Look up actual row # in data fvcd(fvd(row,1)) = 1; % Color base vertices 1st index fvcd(fvd(row,4)) = 1; fvcd(fvd(row,2)) = color; % Assign top vertices color fvcd(fvd(row,3)) = color; end set(ch,‘FaceVertexCData‘, fvcd); % Apply the vertex coloring set(ch,‘EdgeColor‘,‘k‘);
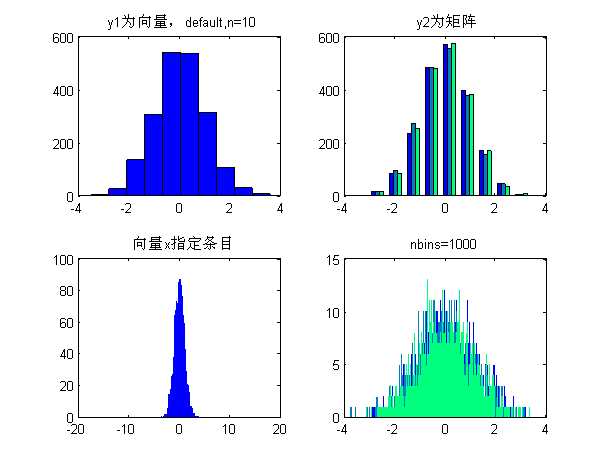
%% 绘制统计直方图 %hist(y):如果y是向量,则把其中元素放入10个条目中,且返回每条中的元素的个数;如果y为矩阵,则分别对每列进行处理,显示多组条形。 %[n,xout]=hist(y,x):非递减向量x的指定bin的中心。向量xout包含频率计数与条目的位置。 x=-10:.1:10; y1=randn(2008,1); y2=randn(2008,3); figure; colormap(winter); subplot(2,2,1); hist(y1);%把其中元素放入10个条目中 title(‘y1为向量,default,n=10‘); subplot(2,2,2); hist(y2);%分别对每列进行处理,显示多组条形 title(‘y2为矩阵‘); subplot(2,2,3); hist(y1,x);%用户也可以使用[n,xout]=hist(y1,x);bar(xout,n)绘制条形直方图 title(‘向量x指定条目‘); subplot(2,2,4); hist(y2,1000);%第二个参数为标量时指定bin的数目 title(‘nbins=1000‘);
%% ========均值方差直方图======== a=[8 9 10 7 8 9];%mean b=[1 1 1 1 1 1];%std figure(); h=bar(a); ch=get(h,‘children‘); set(ch,‘FaceVertexCData‘,[4;2;3;1;5;6]);%使用Indexed形式指定每组bar的颜色 hold on; errorbar(a,b,‘k‘,‘LineStyle‘,‘none‘);
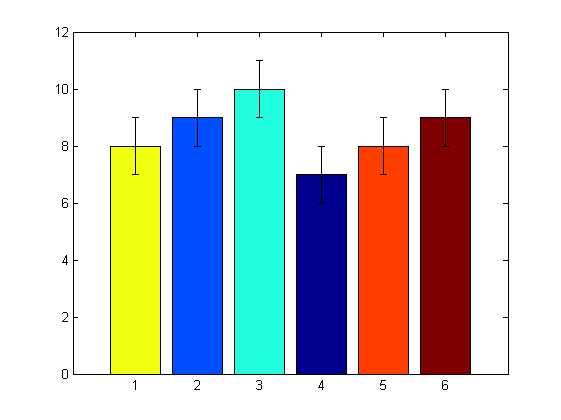
%% =======散点图scatter , scatter3 , plotmatrix====== %scatter3(X,Y,Z,S,C):在由向量X、Y和Z指定的位置显示大小和颜色分别由S和C决定的离散点 figure; [x,y,z] = sphere(16); X = [x(:)*.5 x(:)*.75 x(:)]; Y = [y(:)*.5 y(:)*.75 y(:)]; Z = [z(:)*.5 z(:)*.75 z(:)]; S = repmat([10 2 5]*10,numel(x),1); C = repmat([1 2 3],numel(x),1); subplot(1,2,1); scatter(X(:),Y(:),S(:),C(:)); title(‘scatter‘); subplot(1,2,2); scatter3(X(:),Y(:),Z(:),S(:),C(:),‘filled‘), view(-60,60); title(‘scatter3‘); %plotmatrix(X,Y)绘出X(p*M)与Y(p*N)的列组成的散度图(N,M) figure; X=randn(100,2);Y=randn(100,2); subplot(1,3,1),plotmatrix(X);%等价于plotmatrix(X,X),除了对角上的图为X每一列的直方图hist(X(:,col)) title(‘plotmatrix(X)‘); subplot(1,3,2),plotmatrix(X,X); title(‘plotmatrix(X,X)‘); subplot(1,3,3),plotmatrix(X,Y); title(‘plotmatrix(X,Y)‘);
%% =========绘制区域图=========== %区域图特点是:在图上绘制多条曲线时,每条曲线(除第一条外)都是把“前”条曲线作基线,再取值绘制而成。因此,该指令所画的图形,能醒目地反映各因素对最终结果的贡献份额。 figure; x=1:2:9;% 注意:自变量要单调变化 y=magic(5);% 各因素的相对贡献份额,每一列相当于一个因素 colormap(spring);% 控制图的用色 area(x,y,4);%area(y)则以列下标作为自变量,第三个参数为基准线(默认为0) set(gca,‘layer‘,‘top‘);%图层设置为top层,显示网格 title(‘basevalue=4‘); legend(‘ 因素 A‘,‘ 因素 B‘,‘ 因素 C‘,‘因素D‘,‘因素E‘); grid on;
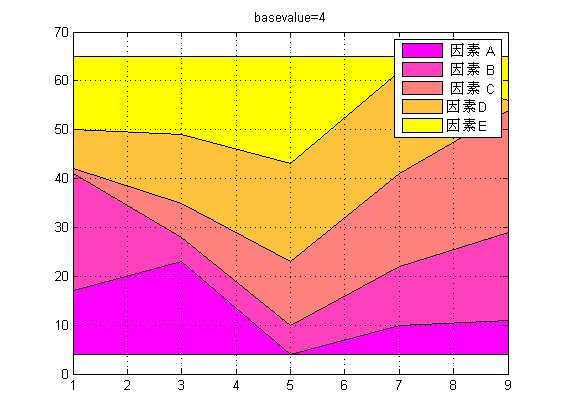
%% =========绘制饼状图========= %饼图指令pie和pie3用来表示各元素占总和的百分数。该指令第二个参数为与第一参数等长的 0-1 %向量,1使对应扇块突出。第三个参数指定个扇区的label figure; colormap(summer);% 控制图的用色 x=[16 17 21 25 21]; subplot(1,2,1); pie(x,[0 0 0 0 1],{‘0-10岁儿童‘,‘10-20岁儿童‘,‘20-35岁青年‘,‘35-55岁中年‘,‘55岁以上老年‘}); subplot(1,2,2); pie3(x,[0 0 0 0 1],{‘0-10岁儿童‘,‘10-20岁儿童‘,‘20-35岁青年‘,‘35-55岁中年‘,‘55岁以上老年‘});
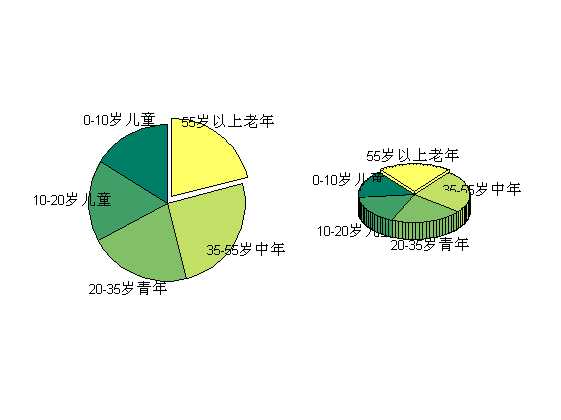
%% 绘制填色多边形。若每列的首尾元素不重合,则将默认把最后一点与第一点相连,强行使多边形封闭。 %fill和fill3用于绘制填色多边形 %fill(X1,Y1,C1,X2,Y2,C2,...) %fill3(X1,Y1,Z1,C1,X2,Y2,Z2,C2,...) %参数1和2为等长向量时,多边形的节点数由项链长度决定;而当其为矩阵时,每一列对应一个多边形 %参数3为颜色(用颜色字符r/g/b/c或[r g b]表示) figure; colormap(autumn);% 控制图的用色 n=10; % 多边形的边数 dt=2*pi/n;t=0:dt:2*pi; t=[t,t(1)]; %fill 指令要求数据向量的首位重合,使图形封闭。 x=sin(t);y=cos(t); subplot(1,2,1); fill(x,y,[1 1 0]);axis off % 画填色多边形,隐去坐标轴。 X=[0.5 0.5 0.5 0.5;0.5 0.5 0.5 0.5;0 1 1 0]; Y=[0.5 0.5 0.5 0.5;0.5 0.5 0.5 0.5;0 0 1 1]; Z=[1 1 1 1;0 0 0 0;0 0 0 0]; C=[1 0 0 1;0 1 0 1;0 0 1 0]; subplot(1,2,2); fill3(X,Y,Z,C); view([-10 55]); xlabel(‘x‘),ylabel(‘y‘);box on;grid on;
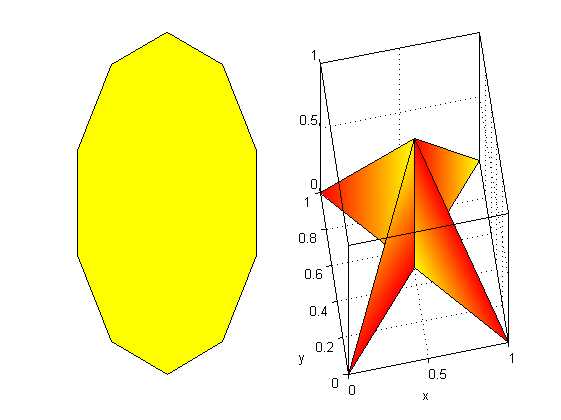
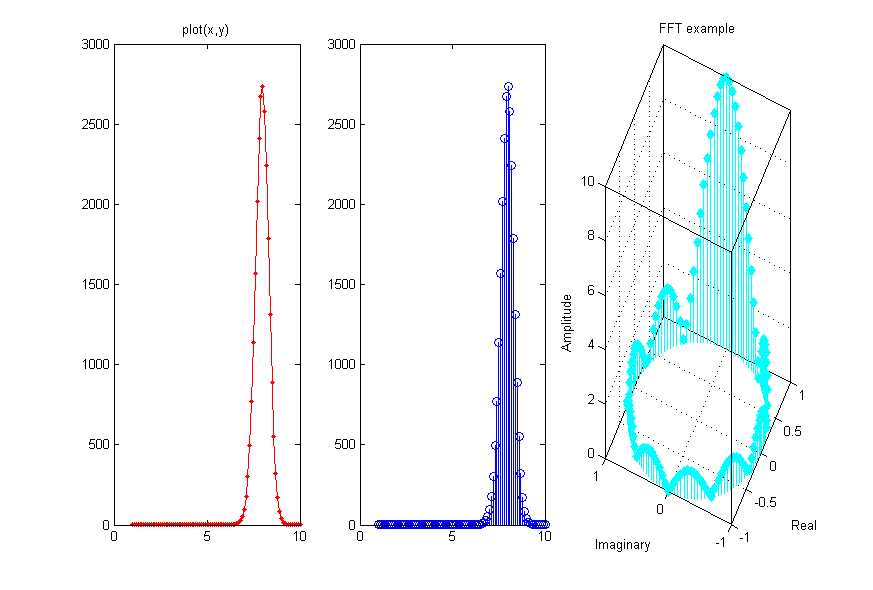
%% =======绘制离散数据杆状图=========== %stem和stem3函数用于绘制二维或三维的离散数据杆状图 %stem(Y)可以理解成绘制离散点的plot(y)函数 %stem(X,Y)可以理解成绘制离散点的plot(x,y)函数 %stem(...,‘filled‘)改变数据点显示的空、实状态。 %stem(...,‘LINESPEC‘)Linespec代表直线属性设置参量。 x=1:.1:10; y=exp(x.*sin(x)); figure; subplot(1,3,1); plot(x,y,‘.-r‘); title(‘plot(x,y)‘); subplot(1,3,2); stem(x,y,‘b‘); subplot(1,3,3); stem(x,y,‘:g‘,‘fill‘); %绘制三维离散杆状图 th=(0:127)/128*2*pi;% 角度采样点 x=cos(th); y=sin(th); f=abs(fft(ones(10,1),128)); %对离散方波进行 FFT 变换,并取幅值 stem3(x,y,f‘,‘cd‘,‘fill‘);%绘制图形 view([-65 30]); xlabel(‘Real‘); %图形标注 ylabel(‘Imaginary‘); zlabel(‘Amplitude‘); title(‘FFT example‘);
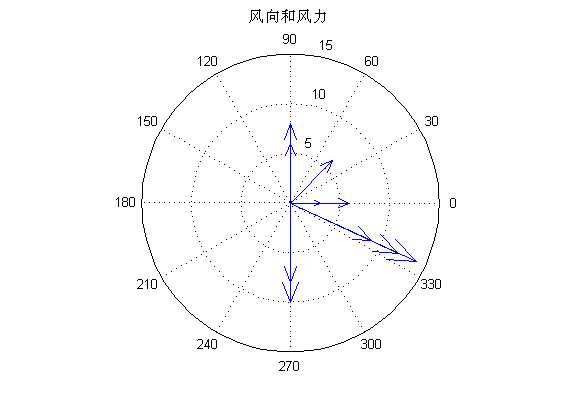
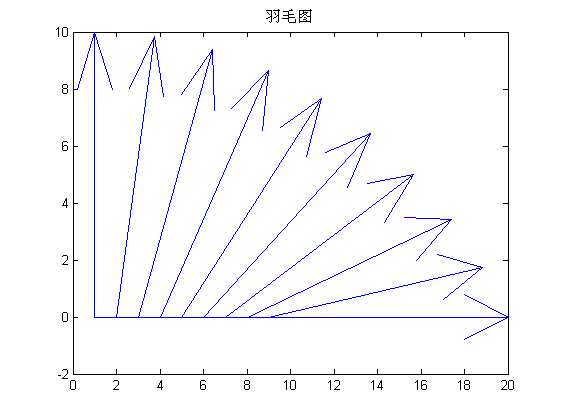
%% =======绘制方向和速度矢量图======= %compass-绘制罗盘图 %feather-绘制羽毛图 %quiver-绘制二维箭头图 %quiver3-绘制三维箭头图 %绘制罗盘图 figure; wdir=[45 90 90 45 360 335 360 270 335 270 335 335]; knots=[6 6 8 6 3 9 6 8 9 10 14 12]; rdir=wdir*pi/180; [x,y]=pol2cart(rdir,knots);% 极坐标转化为直角坐标 compass(x,y); title(‘风向和风力‘) %绘制羽毛图 figure; alpha=90:-10:0; r=ones(size(alpha)); m=alpha*pi/180; n=r*10; [u,v]=pol2cart(m,n);% 极坐标转化为直角坐标 feather(u,v); title(‘羽毛图‘) %罗盘图和羽毛图的比较 figure; t=-pi/2:pi/12:pi/2; % 在 区间,每 取一点。 r=ones(size(t)); % 单位半径 [x,y]=pol2cart(t,r); % 极坐标转化为直角坐标 subplot(1,2,1),compass(x,y),title(‘Compass‘) subplot(1,2,2),feather(x,y),title(‘Feather‘) %绘制箭头图 figure; [x,y] = meshgrid(-2:.2:2,-1:.15:1); z = x .* exp(-x.^2 - y.^2); [px,py] = gradient(z,.2,.15); subplot(1,2,1); contour(x,y,z), hold on quiver(x,y,px,py), hold off, axis image title(‘quiver示例‘); [x,y,z]=peaks(15); [nx,ny,nz]=surfnorm(x,y,z);%surfnorm求平面的法向量 subplot(1,2,2) surf(x,y,z); hold on; quiver3(x,y,z,nx,ny,nz); title(‘quiver3示例‘);
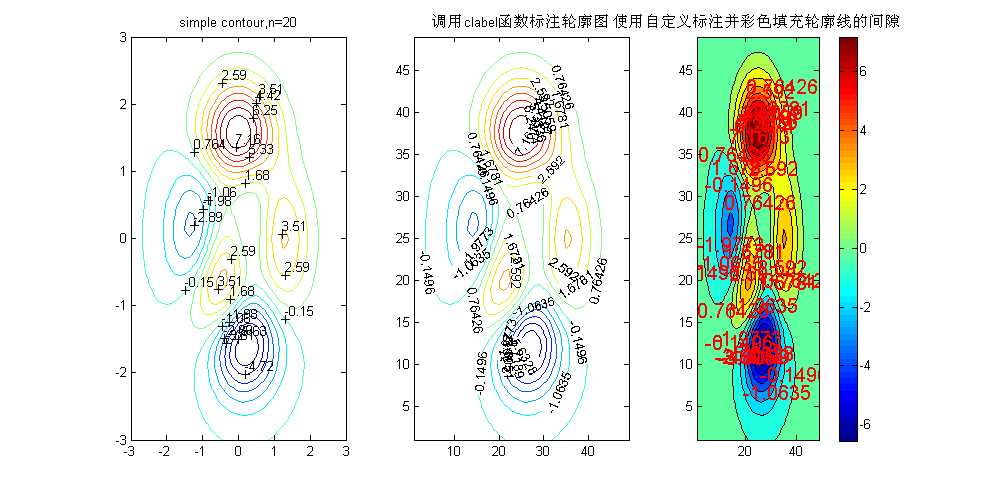
%% ==========轮廓线图的绘制========== %clabel-利用轮廓矩阵生成标签并在当前图形中显示 %contour-利用矩阵所给的值生成二维轮廓线 %contour3-利用矩阵所给的值生成三维轮廓线 %contourf-显示二维轮廓图并用色彩填充个轮廓线的间隙 %contourc-计算被其他轮廓函数占用的轮廓矩阵的低层函数 [x,y,z]=peaks; n=15;% 等高线分级数 figure; subplot(1,3,1); h=contour(x,y,z,n);%绘制20条等高线 clabel(h);%当前图形中显示标签,标签前有‘+‘号且标签会根据轮廓线旋转,每条轮廓线仅有一个标签 title(‘simple contour,n=20‘); subplot(1,3,2); z=peaks; [c,h]=contour(z,n);%绘制15条等高线 clabel(c,h);%标签前无‘+‘号,每天轮廓线可能有多个标签 title(‘调用clabel函数标注轮廓图‘) subplot(1,3,3); z=peaks; [c,h]=contourf(z,n); clabel(c,h,‘FontSize‘,15,‘Color‘,‘r‘,‘Rotation‘,0);%自定义标签 colorbar; title(‘使用自定义标注并彩色填充轮廓线的间隙‘);
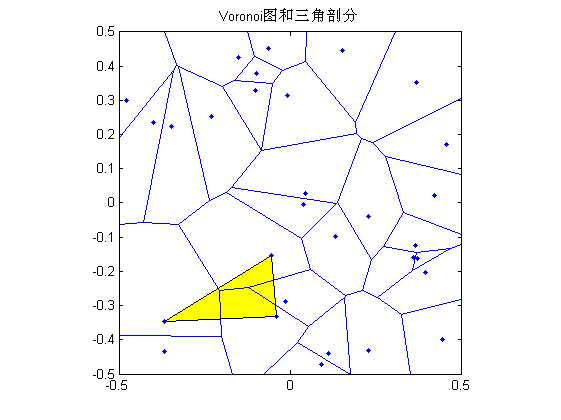
%% ========= Voronoi图和三角剖分======== %用Voronoi多边形勾画每个点的最近邻范围。Voronoi多边形在计算几何、模式识别中有重要应用。三角形顶点所在多边形的三条公共边是剖分三角形边的垂直平分线。 n=30; A=rand(n,1)-0.5; B=rand(n,1)-0.5; % 产生 30 个随机点 T=delaunay(A,B); % 求相邻三点组 T=[T T(:,1)]; %为使三点剖分三角形封闭而采取的措施 voronoi(A,B) % 画 Voronoi 图 hold on;axis square fill(A(T(10,:)),B(T(10,:)),‘y‘); % 画一个剖分三角形 voronoi(A,B) % 重画 Voronoi 图,避免线被覆盖 title(‘Voronoi图和三角剖分‘);
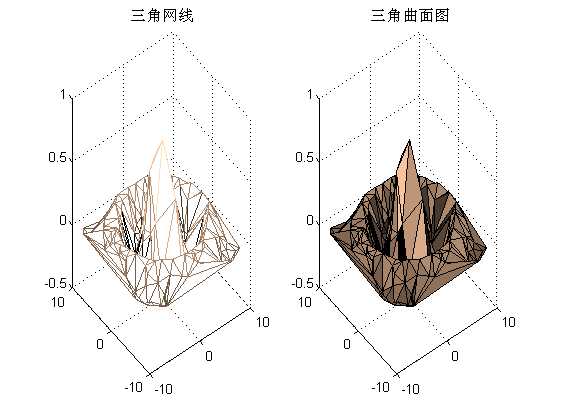
%% =========三角网线和三角曲面图======== figure; X=6*pi*(rand(20,10)-0.5);Y=6*pi*(rand(20,10)-0.5); R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R; tri=delaunay(X,Y); % 进行三角剖分 subplot(1,2,1),trimesh(tri,X,Y,Z); title(‘三角网线‘); subplot(1,2,2),trisurf(tri,X,Y,Z); title(‘三角曲面图‘); colormap(copper);brighten(0.5) % 增强亮度
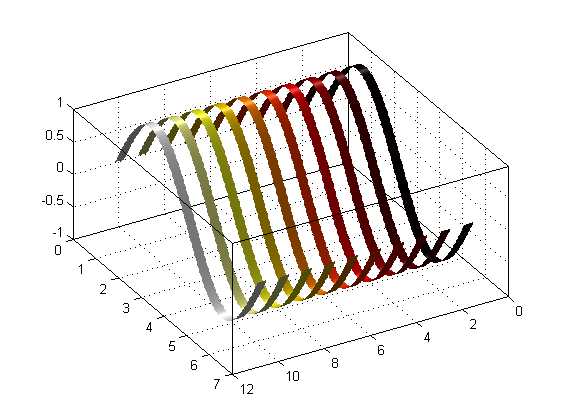
%% ============彩带图ribbon======== %ribbon(X,Y,WIDTH)和plot(X,Y)一样的,只不过每一列在三维中以分开的ribbon绘制 figure; x=0:pi/100:2*pi; x=repmat(x‘,1,10); y=sin(x); ribbon(x,y,0.4);% 画彩带图 % 至此彩带图已经生成。以下指令都是为了使图形效果更好、标识更清楚而用。 view([150,50]),shading interp,colormap(hot)% 设置视角、明暗、色图 light,lighting phong,box on % 设置光源、照射模式、坐标框
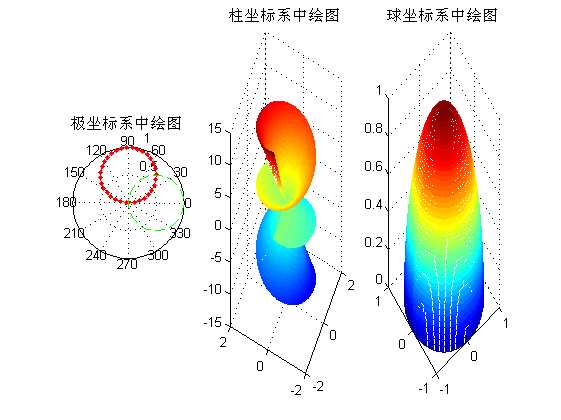
%% ==========在特殊坐标系中绘制特殊图形。======= %利用polar函数在极坐标系中绘制图形 figure; theta=0:.1:pi; rho1=sin(theta); rho2=cos(theta); subplot(1,3,1); polar(theta,rho1,‘.-r‘); hold on; polar(theta,rho2,‘--g‘); title(‘极坐标系中绘图‘); %另外一种和极坐标有关系的坐标系就是柱坐标系了 theta=0:pi/100:3*pi; rho=sin(theta)+cos(theta); [t,r]=meshgrid(theta,rho); z=r.*t; subplot(1,3,2); [x,y,z]=pol2cart(t,r,z);%极坐标系向柱坐标系转化 mesh(x,y,z);%柱坐标系中进行绘图 title(‘柱坐标系中绘图‘); view([-65 30]); %将球坐标系转换为柱面坐标系 subplot(1,3,3); delta=pi/100; theta=0:delta:pi; % theta is zenith angle phi=0:delta:pi; % phi is azimuth angle [t p]=meshgrid(theta,phi); r=ones(size(t)); [x,y,z]=sph2cart(t,p,r);%球坐标向柱坐标转化 mesh(x,y,z);%球坐标系中进行绘图 title(‘球坐标系中绘图‘);
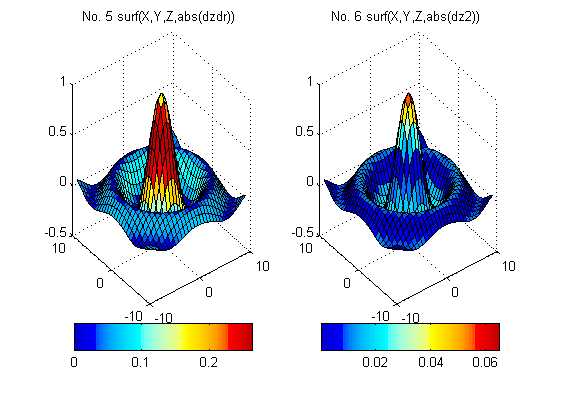
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 %% ======四维表现======== %用色彩表现函数的特征 %当三维网线图、曲面图的第四个输入宗量取一些特殊矩阵时,色彩就能表现或加强函数的某特征,如梯度、曲率、方向导数等。 x=3*pi*(-1:1/15:1);y=x;[X,Y]=meshgrid(x,y); R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R; [dzdx,dzdy]=gradient(Z);dzdr=sqrt(dzdx.^2+dzdy.^2); % 计算对 r 的全导数 dz2=del2(Z); % 计算曲率 figure; subplot(1,2,1),surf(X,Y,Z),title(‘No. 1 surf(X,Y,Z)‘); shading faceted,colorbar( ‘horiz‘) ,brighten(0.2); subplot(1,2,2),surf(X,Y,Z,R),title(‘No. 2 surf(X,Y,Z,R)‘); shading faceted;colorbar( ‘horiz‘); %色彩分别表现函数的高度和半径特征 figure; subplot(1,2,1),surf(X,Y,Z,dzdx) ; shading faceted;brighten(0.1);colorbar( ‘horiz‘); title(‘No. 3 surf(X,Y,Z,dzdx)‘); subplot(1,2,2),surf(X,Y,Z,dzdy); shading faceted;colorbar( ‘horiz‘); title(‘No. 4 surf(X,Y,Z,dzdy)‘); %色彩分别表现函数的 x 方向和 y 方向导数特征 figure; subplot(1,2,1),surf(X,Y,Z,abs(dzdr)) ; shading faceted;brighten(0.6);colorbar( ‘horiz‘); title(‘No. 5 surf(X,Y,Z,abs(dzdr))‘); subplot(1,2,2),surf(X,Y,Z,abs(dz2)); shading faceted;colorbar( ‘horiz‘); title(‘No. 6 surf(X,Y,Z,abs(dz2))‘);
%% ======切片图和切片等位线图======= %利用 slice 和 contourslice 表现 MATLAB 提供的无限大水体中水下射流速度数据 flow 。 flow 是一组定义在三维空间上的函数数据。 %在本例中,从图中的色标尺可知,深红色表示“正速度”(向图的左方),深蓝表示“负速度”(向图的右方)。 % 以下指令用切面上的色彩表现射流速度 [X,Y,Z,V]=flow; % 取 4 个 的射流数据矩阵, V 是射流速度。 x1=min(min(min(X)));x2=max(max(max(X))); % 取 x 坐标上下限 y1=min(min(min(Y)));y2=max(max(max(Y))); % 取 y 坐标上下限 z1=min(min(min(Z)));z2=max(max(max(Z))); % 取 z 坐标上下限 sx=linspace(x1+1.2,x2,5); % 确定 5 个垂直 x 轴的切面坐标 sy=0; % 在 y=0 处,取垂直 y 轴的切面 sz=0; % 在 z=0 处,取垂直 z 轴的切面 figure; slice(X,Y,Z,V,sx,sy,sz); % 画切片图 view([-12,30]);shading interp;colormap jet;axis off;colorbar; % 以下指令用等位线表现射流速度 v1=min(min(min(V)));v2=max(max(max(V))); % 射流速度上下限 cv=linspace(v1,v2,15); % 在射流上下限之间取 15 条等位线 figure; contourslice(X,Y,Z,V,sx,sy,sz,cv);view([-12,30]); colormap jet;colorbar;box on;
下面两段程序均不便上图,自己拿到Matlab里面运行一下看效果吧。
%% =======动态图形========= %简单二维示例-彗星状轨迹图 figure; n=10;t=n*pi*(0:0.0005:1);x=sin(t);y=cos(t); plot(x,y,‘g‘);axis square;hold on comet(x,y,0.01);hold off %卫星返回地球的运动轨线示意 figure; R0=1; % 以地球半径为一个单位 a=12*R0;b=9*R0;T0=2*pi; %T0 是轨道周期 T=5*T0;dt=pi/100;t=[0:dt:T]‘; f=sqrt(a^2-b^2); % 地球与另一焦点的距离 th=12.5*pi/180; % 卫星轨道与 x-y 平面的倾角 E=exp(-t/20); % 轨道收缩率 x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t)); plot3(x,y,z,‘g‘) % 画全程轨线 [X,Y,Z]=sphere(30);X=R0*X;Y=R0*Y;Z=R0*Z; % 获得单位球坐标 grid on,hold on,surf(X,Y,Z),shading interp % 画地球 x1=-18*R0;x2=6*R0;y1=-12*R0;y2=12*R0;z1=-6*R0;z2=6*R0; axis([x1 x2 y1 y2 z1 z2]) % 确定坐标范围 view([117 37]),comet3(x,y,z,0.02),hold off % 设视角、画运动轨线 %色彩变幻‘在 256 色情况下,才可被正确执行.图片刷新可能会卡,单独执行spinmap可查看到效果 figure; peaks; spinmap;
%% =======影片动画 ======= %三维图形的影片动画 figure; shg,x=3*pi*(-1:0.05:1);y=x;[X,Y]=meshgrid(x,y); R=sqrt(X.^2+Y.^2)+eps; Z=sin(R)./R; h=surf(X,Y,Z);colormap(cool);axis off n=12;mmm=moviein(n); %预设画面矩阵。新版完全可以取消此指令 。 for i=1:n rotate(h,[0 0 1],25); %是图形绕 z 轴旋转 25 度 / 每次 mmm(:,i)=getframe; %捕获画面。新版改为 mmm(i)=getframe 。 end movie(mmm,5,10) %以每秒10帧速度,重复播放5次
标签:
原文地址:http://www.cnblogs.com/dongzhuangdian/p/5782030.html