NG课程总结7

标签：

七、神经网络

1.在参数很多时，非线性假说有弊端。

   eg:

   假设有3个特征值，含所有二次项的h为h=(θ0+θ1*x1^2+θ2*x1x2+θ3*x1x3+θ4*x2^2+θ5*x2x3+θ6*x3^2)

   假设有n个特征值，若h含所有二次项，那么h的项数可近似为Ο(n^2 /2)

   假设有n个特征值，若h含所有三次项，那么h的项数可近似为Ο(n^3)

   由此可见，若n很大，项数会太多变得复杂，由此引入神经网络，它借鉴一部分生物学理论，神经可塑性(neuroplasticity)

2.模型

• 输入：(x1,x2...xn),加上一个x0=1 (bias unit)
• 逻辑函数：和归类中的一样，在这里也称为sigmoid (logistic) activation function

          (参数theta在这里称为权重)

• 简化形式：

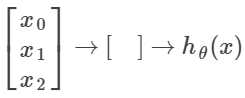
         输入层   隐藏层   输出层

         层1       层2       层3

         将隐藏层的结点标为a1,a2...an,称作活化单元(activation units),那么：

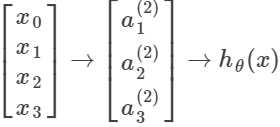
         设标号如下：

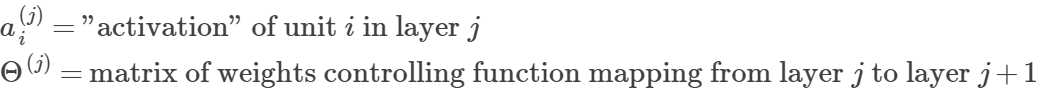
          其中Θ(j)是第j层的权值矩阵,它的维度如下：

         中间层的a便是这样求得的：

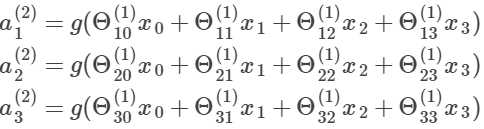           ( 这个theta矩阵为Θ(2) )

         我们最终要求的h(x)为：

3.向量化实现：

•  ：表示g()函数内部的变量

  　　  eg:

  　　  第二层的结点k便为：

• x,z(j)向量表示：

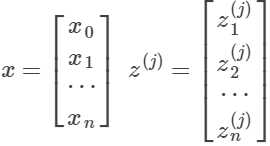
       令x=a(1),则：

           (j>=2)

        再给a(j)加上bias unit =1,那么就可以求下一个z向量：

        如此不断的求，最终的输出只有一个值，也就是只有一行，那么最后的结果就是：

4.一些例子：

• 实现逻辑与函数：

        图大概如下：

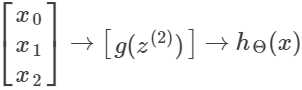          (x0=1)

        若令：

        那么：

• 用与、或、非或构造非异或(两数相同为1，不同为0)：

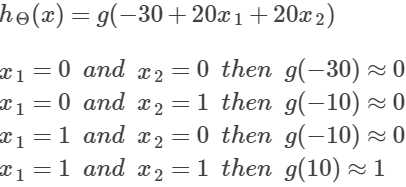
        首先实现与、非或、或需要的参数如下：

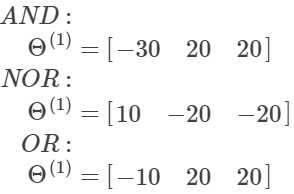
         图大概如下：

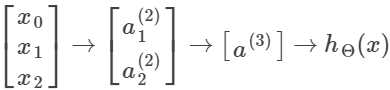
         构造权重矩阵如下：

                    (可以设两个参数代入逻辑公式验算一下，可得出非异或的结果)

         将a全都写出来，可得结果：

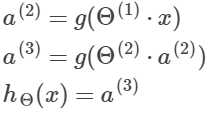
5.实现多归类问题：

   eg:分成4类

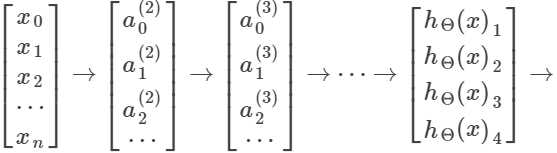
    那么，=

    ，依此类推，下标代表属于第几个类

    最终的结果的集合为：

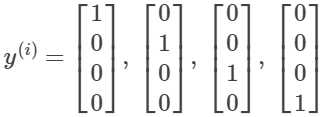
    最终的h为其中的一个元素

NG课程总结7

标签：

原文地址：http://www.cnblogs.com/cherry-yue/p/5785021.html