标签:class blog img width javascript java div code com size strong
一、Cohen-Sutherland剪裁算法
1.基本思想
对于每条线段P1P2分为三种情况处理:
(1)若P1P2完全在窗口内,则显示该线段P1P2。
(2)若P1P2明显在窗口外,则丢弃该线段。
(3)若线段不满足(1)或(2)的条件,则在交点处把线段分为两段。其中一段完全在窗口外,可弃之。然后对另一段重复上述处理。
为快速判断,采用如下编码方法:
将窗口边线两边沿长,得到九个区域,每一个区域都用一个四位二进制数标识,直线的端点都按其所处区域赋予相应的区域码,用来标识出端点相对于裁剪矩形边界的位置
2.算法流程
3.交点求取
计算线段P1(x1,y1)--P2(x2,y2)与窗口边界的交点
if ( LEFT &code !=0 )
{ x=XL; y=y1+(y2-y1)*(XL-x1)/(x2-x1);}
else if ( RIGHT & code !=0 )
{ x=XR; y=y1+(y2-y1)*(XR-x1)/(x2-x1);}
else if ( BOTTOM & code !=0 )
{ y=YB; x=x1+(x2-x1)*(YB-y1)/(y2-y1);}
else if ( TOP & code !=0 )
{ y=YT; x=x1+(x2-x1)*(YT-y1)/(y2-y1);}
二、Sutherland-Hodgman剪裁算法
1.基本思想
分割处理策略:将多边形关于矩形窗口的裁剪分解为多边形关于窗口四边所在直线的裁剪。
流水线过程(左上右下):前边的结果是后边的输入。
三、 程序流程图
一、Cohen-Sutherland算法
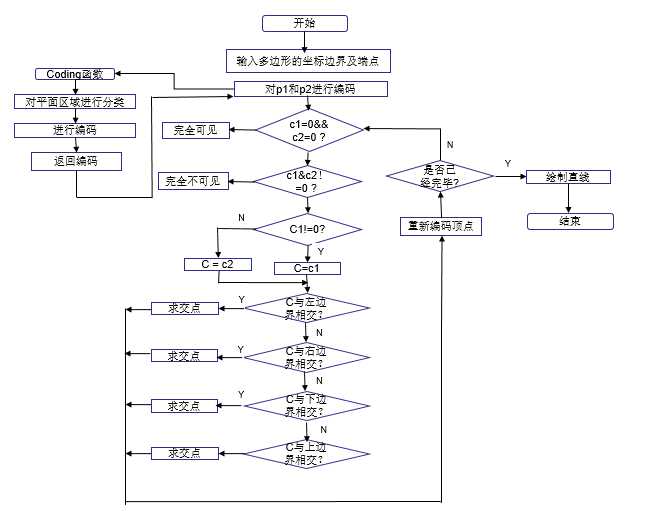
二、Sutherland-Hodgman算法
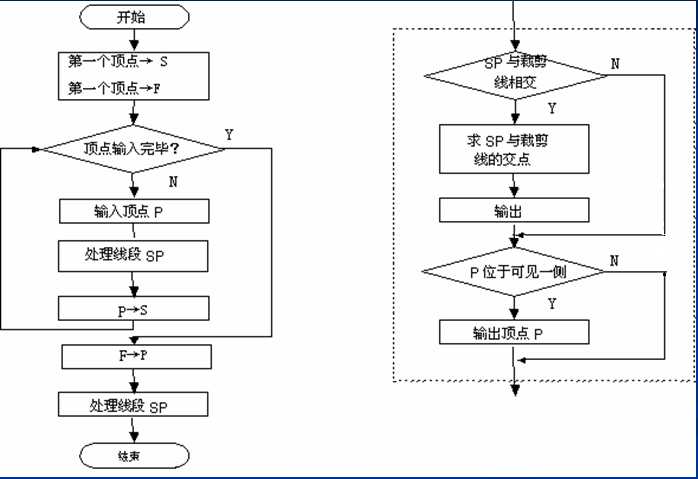
四、源程序
一、Cohen-Sutherland
1 #include "easyx.h" 2 #include "math.h" 3 #include "windows.h" 4 #include "stdio.h" 5 #include "stdlib.h" 6 #include "conio.h" 7 #include "graphics.h" 8 9 #define left 1 10 #define right 2 11 #define bottom 8 12 #define top 4 13 14 int edge_x1,edge_x2,edge_y1,edge_y2; //全局变量,代表剪裁的边界 15 16 //画线算法 17 void dda(int x1,int y1,int x2,int y2,int color) 18 { 19 int steps; 20 double xin,yin,dx,dy,x,y; 21 dx = x2 - x1; 22 dy = y2 - y1; 23 if(fabs(dx) > fabs(dy)) 24 steps = fabs(dx); 25 else 26 steps = fabs(dy); 27 xin = (double)(dx/steps); 28 yin = (double)(dy/steps); //possible loss of data 29 x = x1; 30 y = y1; 31 putpixel(x,y,color); 32 for(int i = 0;i <= steps;i ++) 33 { 34 x = x + xin; 35 y = y + yin; 36 putpixel(x,y,color); 37 } 38 } 39 40 41 //对输入的点进行编码 42 int coding(int x,int y) 43 { 44 int code; 45 if(y <= edge_y2 && y >= edge_y1) 46 { 47 if(x > edge_x2) 48 code = 2; //中右方 49 else if(x < edge_x1) 50 code = 1; //中左方 51 else 52 code = 0; //中心 53 } 54 55 else if(y > edge_y2) 56 { 57 if(x > edge_x2) 58 code = 6; //右下方 59 else if(x < edge_x1) 60 code = 5; //左下方 61 else 62 code = 4; //中下方 63 } 64 else 65 { 66 if(x > edge_x2) 67 code = 10; //右上方 68 else if(x < edge_x1) 69 code = 9; //左上方 70 else 71 code = 8; //中上方 72 } 73 74 return code; 75 } 76 77 78 79 80 //剪裁算法 81 int cutline(int x1,int y1,int x2,int y2) 82 { 83 int visible = 0,done = 1; 84 int c; 85 int c1,c2; 86 int x,y; //表示交点 87 c1 = coding(x1,y1); 88 c2 = coding(x2,y2); //将顶点进行编码 89 do 90 { 91 if(c1 == 0 && c2 == 0) //完全可见 92 { 93 visible = 1; 94 done = 0; 95 } 96 else if((c1 & c2) != 0) //完全不可见 97 { 98 done = 0; 99 } 100 else 101 { 102 //////////////////////////// 103 if(c1 != 0) 104 c = c1; 105 else 106 c = c2; 107 //////////////////////////// 108 if((left & c) != 0) 109 { 110 x = edge_x1; 111 y = y1 + (y2 - y1)*(edge_x1 - x1)/(x2-x1); 112 } 113 else if((right & c) != 0) 114 { 115 x = edge_x2; 116 y = y1 + (y2 - y1)*(edge_x2 - x1)/(x2-x1); 117 } 118 else if((bottom &c )!= 0) 119 { 120 y = edge_y1; 121 x = x1 + (x2 - x1)*(edge_y1 - y1)/(y2-y1); 122 } 123 else if((top & c )!= 0) 124 { 125 y = edge_y2; 126 x = x1 + (x2 - x1)*(edge_y2 - y1)/(y2-y1); 127 } 128 else 129 {} 130 ////////////////////////////////////// 131 if(c = c1) 132 { 133 x1 = x; 134 y1 = y; 135 c1 = coding(x1,y1); 136 } 137 else 138 { 139 x2 = x; 140 y2 = y; 141 c2 = coding(x2,y2); 142 } 143 /////////////////////////////////// 144 }//else 145 146 }while(done); //while 147 148 dda(x1,y1,x2,y2,RGB(0,0,255)); //画线 149 150 return 0; 151 } 152 153 154 int main() 155 { 156 //硬件测试,将gd装入图形驱动器,gm置入最大图形模式。 157 int gd=DETECT,gm; 158 int x1,y1,x2,y2; 159 //输入X的边界 160 printf("请输入剪裁区域的横坐标边界\n"); 161 printf("X1 = "); 162 scanf("%d",&edge_x1); 163 printf("\n"); 164 printf("X2 = "); 165 scanf("%d",&edge_x2); 166 printf("\n\n"); 167 168 //输入Y的边界 169 printf("请输入剪裁区域的纵坐标边界\n"); 170 printf("Y1 = "); 171 scanf("%d",&edge_y1); 172 printf("\n"); 173 printf("Y2 = "); 174 scanf("%d",&edge_y2); 175 printf("\n\n"); 176 177 //输入直线端点 178 printf("请输入直线两个顶点的坐标"); 179 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 180 181 //图形初始化 182 initgraph(&gd,&gm,"c:\\tc"); 183 //设置兰背景。 184 setbkcolor(WHITE); 185 cleardevice(); 186 187 cutline(x1,y1,x2,y2); //进行剪裁 188 189 getch(); 190 closegraph(); 191 return 0; 192 }
二.Sutherland-Hodgman
1 #include "easyx.h" 2 #include "math.h" 3 #include "windows.h" 4 #include "stdio.h" 5 #include "stdlib.h" 6 #include "conio.h" 7 #include "graphics.h" 8 9 int edge_x1,edge_x2,edge_y1,edge_y2; //全局变量,代表剪裁的边界 10 11 //画线算法 12 void dda(int x1,int y1,int x2,int y2,int color) 13 { 14 int steps; 15 double xin,yin,dx,dy,x,y; 16 dx = x2 - x1; 17 dy = y2 - y1; 18 if(fabs(dx) > fabs(dy)) 19 steps = fabs(dx); 20 else 21 steps = fabs(dy); 22 xin = (double)(dx/steps); 23 yin = (double)(dy/steps); //possible loss of data 24 x = x1; 25 y = y1; 26 putpixel(int(x),int(y),color); 27 for(int i = 0;i <= steps;i ++) 28 { 29 x = x + xin; 30 y = y + yin; 31 putpixel(int(x),int(y),color); 32 } 33 } 34 35 //剪裁算法 36 int Surtherland_Hondgman(double p[][2],int n,int bound) 37 { 38 int sumpoint = 0; //新的顶点个数 39 double new_p[100][2]; //存放新的顶点序列 40 double sx = p[n-1][0],sy = p[n-1][1]; //将定点序列的最后一个顶点赋值给s 41 int flag; 42 if(sx > bound) //在内侧 43 flag = 0; 44 else 45 flag = 1; 46 47 for(int i = 0;i < n;i++) 48 { 49 if(p[i][0] > bound) //在内侧 50 { 51 if(flag != 0) 52 { 53 flag = 0; 54 //求交点并放入新的多边形顶点序列中; 55 new_p[sumpoint][0] = bound; //横坐标 56 new_p[sumpoint][1] = sy + (((p[i][1] - sy)/(p[i][0] - sx)) * (bound - sx)); //纵坐标 57 sumpoint++; 58 } 59 new_p[sumpoint][0] = p[i][0]; 60 new_p[sumpoint][1] = p[i][1]; //将当前顶点放入新的多边形顶点序列new_p中 61 sumpoint++; 62 } 63 else 64 { 65 if(flag == 0) 66 { 67 flag = 1; 68 new_p[sumpoint][0] = bound; //横坐标 69 new_p[sumpoint][1] = sy + (((p[i][1] - sy)/(p[i][0] - sx)) * (bound - sx)); //纵坐标 70 sumpoint++; 71 } 72 } 73 sx = p[i][0]; 74 sy = p[i][1]; 75 } 76 for(int i = 0;i < sumpoint-1;i++) 77 dda(new_p[i][0],new_p[i][1],new_p[i+1][0],new_p[i+1][1],RGB(255,0,0)); 78 dda(new_p[0][0],new_p[0][1],new_p[sumpoint-1][0],new_p[sumpoint-1][1],RGB(255,0,0)); 79 80 return 0; 81 } 82 83 84 int main() 85 { 86 //硬件测试,将gd装入图形驱动器,gm置入最大图形模式。 87 int gd=DETECT,gm; 88 int n; 89 double p[10][2]; 90 //输入X的边界 91 printf("请输入剪裁区域的左侧边界的横坐标\n"); 92 printf("X1 = "); 93 scanf("%d",&edge_x1); 94 95 //dda(edge_x1,1,edge_x1,500,BLUE); 96 97 //输入直线端点 98 printf("请输入待剪裁多边形的边数:"); 99 scanf("%d",&n); 100 printf("请输入待剪裁多边形的顶点序列:\n"); 101 for(int i = 0;i < n;i ++) 102 scanf("%lf%lf",&p[i][0],&p[i][1]); 103 104 105 //图形初始化 106 initgraph(&gd,&gm,"c:\\tc"); 107 //设置兰背景。 108 setbkcolor(WHITE); 109 cleardevice(); 110 111 Surtherland_Hondgman(p,n,edge_x1); //先对左边界进行裁剪 112 113 getch(); 114 closegraph(); 115 return 0; 116 }
图形学_二维图形的剪裁_Sutherland-Hodgeman_Cohen—Sutherland,布布扣,bubuko.com
图形学_二维图形的剪裁_Sutherland-Hodgeman_Cohen—Sutherland
标签:class blog img width javascript java div code com size strong
原文地址:http://www.cnblogs.com/baichenjia/p/3694727.html