《Numerical Methods》-chaper7-解线性方程组的直接方法和最小二乘问题

标签：

  基于我们在线性代数中学习过的知识，我们知道解线性方程组本质上就是Gauss消元，也就是基于增广矩阵A的矩阵初等变换。关于数学层面的内容这里不做过多的介绍，这里的侧重点是从数值计算的角度来看这些常见的问题。

  那么基于Gauss消元的算法，我们将会很好理解如下的Matlab代码：

  for j = 1:n-1

   for i = j+1 : n

     mult = A(i,j)/A(j,j);

A(i,:) = A(i,:) – mult*A(j,:);    %这里改写成A(i , j:n) = A(i,j:n) – mult*A(j,j:n)效率更高

b(i) = b(i) – mult*b(j);         %这里的b是增光矩阵的最右一列向量，也就是方程组右侧常数部分

end;

end;

  这我们能够明显的看到，由于这里计算mult的时候涉及除法，所以无法处理A(j,j)=0的情况。

  关于这种一般化的Gauss消元，进行如下的时间复杂度的分析，这里我们以进行多少次浮点运算为衡量标准。

  写法1 ：

A(i,:) = A(i,:) – mult*A(j,:);

这种情况下，进行的浮点运算数如下：

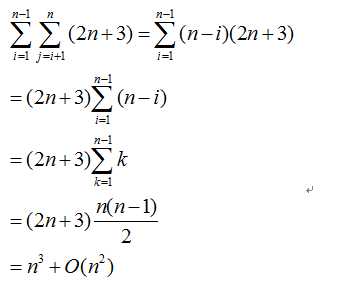
写法2：

  A(i , j:n) = A(i,j:n) – mult*A(j,j:n)

  这种写法相对第一种写法的优化，体现在在处理每一行的时候，自动跳过了该行前面为0的元素，以减少浮点运算的次数。

  它的运算次数计算过程如下：

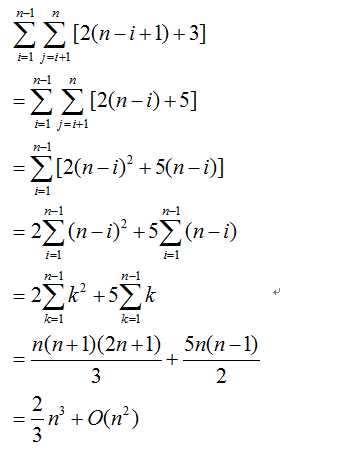
  这里进行了相当精确的计算，可以看到，对于n x n的系数矩阵，完成Guess消元至少也需要进行n的三次方次浮点运算。

  承接上面对Guess消元算法的详细运算复杂度的分析，我们在分析时间复杂度的时候，往往会需要计算如下的一个和式：

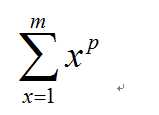
  这里就简单的介绍一下这个和式的一个估算方法。

  我们利用幂函数与x轴围成的面积，使用一个类似夹逼准则的手法，来对这个和式进行估算。

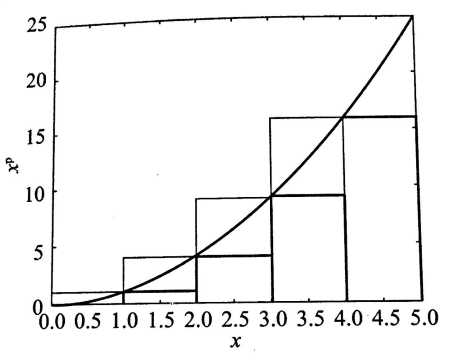
  我们将幂函数y = x^p，横坐标取m份，间距为1。

  那么和式其实就是图中矩阵的和，那么我们很容易能够看到如下的一个不等式成立：

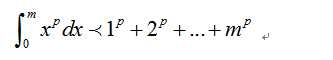
  而这里我们观察前4个矩形上面的小矩形，他们和实际上等于第5个矩形，因此我们容易看到如下的不等式：

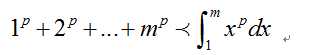
  因此这个和式成功的被两个定积分给“夹逼”了，下面分别求定积分。

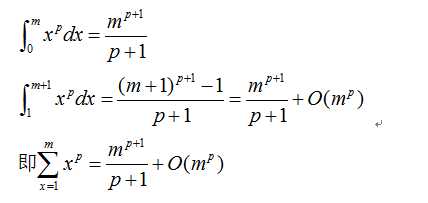
《Numerical Methods》-chaper7-解线性方程组的直接方法和最小二乘问题

标签：

原文地址：http://www.cnblogs.com/rhythmic/p/5789448.html