标签:
二维数组查找
题目描述:
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。
请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
1、暴力搜索(简称"暴搜") public class Solution { public boolean Find(int [][] array,int target) { for(int i = 0; i < array.length; ++i) { for(int j = 0; j < array[i].length; ++j) { if(array[i][j] == target) { return true; } } } return false; } }
算法分析:
这种方法简单粗暴,初学者往往首先想到。渐进时间复杂度O(n^2),数据量大时搜索效率较低。
2、二分搜索
public class Solution { public boolean Find(int [][] array,int target) { // 分行二分搜索 for(int i = 0; i < array.length; ++i) { int left = 0; int right = array[i].length - 1; while(left <= right) { int mid = (left + right) >>> 1; if(array[i][mid] < target) { left = mid + 1; } else if(array[i][mid] > target) { right = mid - 1; } else { return true; } } } return false; } }
算法分析:
由于二维数组按行、列具有递增(有序),因此可在暴搜算法的基础上使用二分搜索进行优化。此算法的渐进时间复杂度为O(n*log2(n)),显然O(n^n) > O(n*log2(n))。
3、不知道该叫什么算法,反正有点智力题的味道
public class Solution { public boolean Find(int [][] array,int target) { // 从左下角位置开始搜索(向上减少,向右增加,分岔点) int row = array.length - 1; int col = 0; // 边界检查 while(row >= 0 && col < array[0].length) { if(array[row][col] < target) { col ++; } else if(array[row][col] > target){ row --; } else { return true; } } return false; } }
算法分析:
算法渐进时间复杂度进一步降低,为O(n)。
这种算法在处理这道题目时存在缺陷,只能够处理矩阵,而不能够完美兼容不规则二维数组。
当然,本题如果从右上角开始搜索也是同理。
算法分析
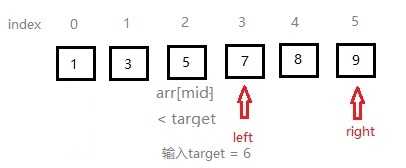
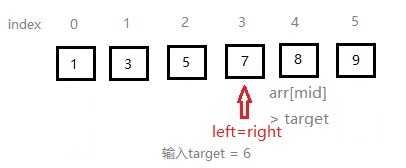
二分搜索算法(binary search algorithm)代码:
public static boolean binarySearch(int[] arr, int target) { int low = 0; int high = arr.length - 1; while(low <= high) { int mid = (low + high) >>> 1; if(arr[mid] < target) { low = mid + 1; } else if(arr[mid] > target) { high = mid - 1; } else { return true; } } return false; }
二分搜索具体分析:

标签:
原文地址:http://www.cnblogs.com/forget406/p/5790412.html