一个实例学会LINGO之选址问题

标签：

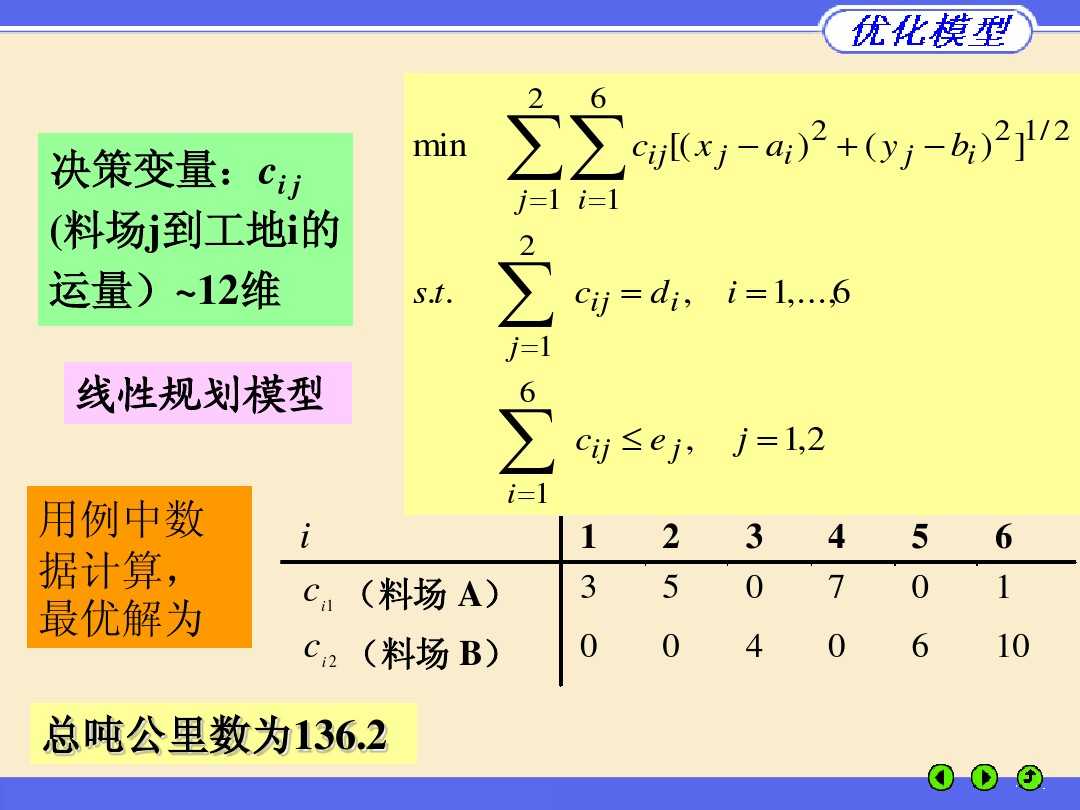
代码如下：

!选址问题;
!吨公里和运费成正比;

MODEL:

Title Location Problem;

sets:
demand/1..6/:a,b,d;!定义a,b,d三个向量，大小为1x6;
supply/1..2/:x,y,e;
link(demand,supply):c;!定义c为一个矩阵，稠密集合，所以大小为demand x supply 即6x2;
endsets

data:
a=1.25,8.75,0.5,5.75,3,7.25;!工地横坐标;
b=1.25,0.75,4.75,5,6.5,7.75;!工地纵坐标;
d=3,5,4,7,6,11;!工地需求量;
e=20,20;!供给量;
enddata

init:!initial location for the supply(初始点)，赋初始值;
x,y=5,1,2,7;!仓库位置（5，2）和（1，7）;
endinit

min=@sum(link(i,j):c(i,j)*((x(j)-a(j))^2+(y(j)-b(i))^2)^(1/2));
@for(demand(i):[DEMAND_CON]@sum(supply(j):c(i,j))=d(i););
@for(supply(i):[SUPPLY_CON]@sum(demand(j):c(j,i))<=e(i););
@for(supply:@free(X);@free(Y););

END

LINGO的代码就是如此简洁，它可以又好又快地解决许多数学问题，感兴趣的同学要把这个代码看懂哦，这个还算比较典型，如果有疑问，

可以致电我的邮箱：lovetayloryu@gmail.com

如果你对ICT(Information Communications Technology）或者数学建模感兴趣，可以与我交流哈。

小编是一个敢大胆尝试新东西的ICT keener 也是一只萌萌哒95后单身喵~lol

一个实例学会LINGO之选址问题

标签：

原文地址：http://www.cnblogs.com/lemonCyu/p/5791219.html