码迷，mamicode.com
首页 > 其他好文 > 详细

优化DP的奇淫技巧

时间：2016-08-21 16:32:52      阅读：251      评论：0      收藏：0      [点我收藏+]

标签：

DP是搞OI不可不学的算法。一些丧心病狂的出题人不满足于裸的DP，一定要加上优化才能A掉。

故下面记录一些优化DP的奇淫技巧。
裸的状态方程很好推。
f[i]=max(f[j]+sum[i]-sum[j]-100*I) (1<=j<i&&f[j]>=100*i)
然后把无关于j的提出来。
f[i]=max(f[j]-sum[j])+sum[i]-100*i;
好的，现在只需要把在O(1)的时间内求出max(f[j]-sum[j])就是坠吼得。
考虑两个决策f[j] f[k](j>k)
j决策比k决策优当且仅当
f[j]-sum[j]>=f[k]-sum[k]
f[j]-f[k]>=sum[j]-sum[k]
然后单调队列加成。O(N)就能求出答案。
 
//OJ 1326
//by Cydiater
//2016.8.8
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <iomanip>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
const int MAXN=2e6+5;
const int oo=0x3f3f3f3f;
inline ll read(){
      char ch=getchar();ll x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
ll N,M,f[MAXN],q[MAXN],head=1,tail=0,sum[MAXN];
namespace solution{
      void init(){
            N=read();M=read();
            memset(sum,0,sizeof(sum));
            up(i,1,N)sum[i]=read()+sum[i-1];
      }
      void dp(){
            memset(f,0,sizeof(f));
            f[0]=M;q[++tail]=0;
            up(i,1,N){
                  while(head<tail&&f[q[head]]<100*i)head++;
                  int id=q[head];
                  f[i]=f[id]+sum[i]-sum[id]-i*100;
                  while(head<=tail&&f[i]-f[q[tail]]>=sum[i]-sum[q[tail]])tail--;
                  q[++tail]=i;
            }
      }
      void output(){
            printf("%I64d\n",f[N]);
      }
}
int main(){
      //freopen("input.in","r",stdin);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

OJ1327

和上一题差不多，对于每个i都要维护一个单调队列
//OJ 1327
//by Cydiater
//2016.8.8
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <cstdlib>
#include <iomanip>
#include <ctime>
#include <cmath>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
const int MAXN=1e4+5;
const int oo=0x3f3f3f3f;
inline int read(){
      char ch=getchar();int x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
int N,M,S,u[MAXN],d[MAXN],q[105][MAXN],head[105],tail[105],f[105][MAXN];
namespace solution{
      void init(){
            memset(f,10,sizeof(f));
            N=read();M=read();S=read();
            up(i,1,N)u[i]=read();
            up(i,1,N)d[i]=read();
      }
      void dp(){
            f[0][0]=0;
            up(i,0,100)head[i]=1,tail[i]=0;
            q[0][++tail[0]]=0;
            up(i,1,N)down(j,S,0){
                  while(head[i-1]<tail[i-1]&&q[i-1][head[i-1]]>u[i]+j)head[i-1]++;
                  f[i][j]=f[i-1][q[i-1][head[i-1]]]+(M-d[i])*q[i-1][head[i-1]]+(u[i]+j)*d[i];
                  while(f[i][q[i][tail[i]]]+(M-d[i+1])*q[i][tail[i]]>=f[i][j]+(M-d[i+1])*j&&head[i]<=tail[i])tail[i]--;
                  q[i][++tail[i]]=j;
            }
      }
      void output(){
            printf("%d\n",f[N][0]);
      }
}
int main(){
      freopen("input.in","r",stdin);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

原来这就是斜率优化
 
这道题的dp次序可以是升序的或者是降序的，这道题如果比较过升序和降序的DP方程的话显然降序是比较简便的DP次序。
 
然后可以得到这样的方程。T F表示前缀和，从N->1
f[i]=min{f[j]+(T[i]-T[j]+S)*F[i]} i<j<=N
简化DP方程
f[i]=min{f[j]-T[j]*F[i]}+(T[i]+S)*F[i] i<j<=N
那么设置决策x<y
如果x决策比y决策优，那么
f[x]-T[x]*F[i]<=f[y]-T[y]*F[i]
f[x]-f[y]<=T[x]*F[i]-T[y]*F[i]
(f[x]-[y])/(T[x]-T[y])<=F[i]
这样已经是化简的极限了，对于左边那一坨类似于斜率的东西，来进行斜率优化
设i<x<y<z<=N
设g(x,y)=(f[x]-[y])/(T[x]-T[y])
如果g(x,y)<g(y,z) 那么y决策没有x和z决策优
因为如果
1.g(x,y)<=F[i] ==> x比y优
2.g(y,z) >F[i] ==>z比y优
 
然后维护一个队列就行了
 
//OJ 1328
//by Cydiater
//2016.8.9
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <cstdlib>
#include <cstdio>
#include <ctime>
#include <cmath>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
const int MAXN=5005;
const int oo=0x3f3f3f3f;
inline int read(){
      char ch=getchar();int x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
int N,S,F[MAXN],T[MAXN],a[MAXN],b[MAXN],f[MAXN],q[MAXN],head,tail;
namespace solution{
      void init(){
            N=read();S=read();
            up(i,1,N){
                  a[i]=read();b[i]=read();
            }
            F[N+1]=T[N+1]=0;
            down(i,N,1){
                  T[i]=T[i+1]+a[i];
                  F[i]=F[i+1]+b[i];
            }
      }
      inline double K(int x,int y){return 1.0*(f[x]-f[y])/(1.0*(T[x]-T[y]));}
      void dp(){
            head=1;tail=0;q[++tail]=0;
            down(i,N,1){
                  while(head<tail&&K(q[head+1],q[head])<F[i])head++;
                  f[i]=f[q[head]]-T[q[head]]*F[i]+(T[i]+S)*F[i];
                  while(head<tail&&K(i,q[tail])<K(q[tail],q[tail-1]))tail--;
                  q[++tail]=i;
            }
      }
      void output(){
            cout<<f[1]<<endl;
      }
}
int main(){
      //freopen("input.in","r",stdin);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

同样是斜率优化的经典题目。题解都有，不放了
 
//OJ 1329
//by Cydiater
//2016.8.9
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <map>
#include <algorithm>
#include <cmath>
#include <ctime>
#include <cstdlib>
#include <iomanip>
#include <string>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
#define FILE "bzoj_1010"
const int MAXN=5e4+5;
const int oo=0x3f3f3f3f;
inline ll read(){
      char ch=getchar();ll x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
ll N,L,a[MAXN],f[MAXN],q[MAXN],head=1,tail=0;
namespace solution{
      inline double Q(int x){return a[x]+1.0*x;}
      inline double P(int x){return Q(x)-L-1;}
      inline double col(int x,int y){
            double tmp2=f[y]+Q(y)*Q(y);
            double tmp1=f[x]+Q(x)*Q(x);
            return (tmp2-tmp1)/(Q(y)-Q(x));
      }
      void init(){
            N=read();L=read();
            memset(a,0,sizeof(a));
            up(i,1,N)a[i]=read()+a[i-1];
      }
      void dp(){
            q[++tail]=0;
            up(i,1,N){
                  while(head<tail&&col(q[head],q[head+1])<2*P(i))head++;
                  f[i]=f[q[head]]+(P(i)-Q(q[head]))*(P(i)-Q(q[head]));
                  while(head<tail&&col(q[tail-1],q[tail])>col(q[tail],i))tail--;
                  q[++tail]=i;
            }
      }
      void output(){
            cout<<f[N]<<endl;
      }
}
int main(){
      //freopen("input.in","r",stdin);
      freopen(FILE".in","r",stdin);
      freopen(FILE".out","w",stdout);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

依然是人民群众喜闻乐见的斜率优化。
刚开始以为土地顺序必须是固定的...
然后就很傻叉的推了半小时DP方程，无果
去搜了搜题解才发现土地顺序并不是固定的..
 
不废话，说正解
首先排序，以leftt为第一关键字降序，rightt为第二关键字升序/降序 
然后就能够找出所有可能对答案有贡献的土地
这时候对于所有的leftt显然是降序，对于所有的rightt显然是升序
然后就可以得到
f[i]=min{f[j]+leftt[j+1]*rightt[i]}
最后推出来:
(f[y]-f[x])/(leftt[x+1]-leftt[y+1])<=rightt[i] x<y
y比x优，然后维护一个下凸包就行了。
 
//OJ 1330
//by Cydiater
//2016.8.9
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <map>
#include <algorithm>
#include <ctime>
#include <cmath>
#include <iomanip>
#include <cstring>
#include <string>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
typedef pair<ll,ll> pll;
const int MAXN=5e4+5;
const int oo=0x3f3f3f3f;
inline ll read(){
      char ch=getchar();ll x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
ll N,cnt=0,q[MAXN],head=1,tail=0,f[MAXN];
pll t[MAXN],a[MAXN];
namespace solution{
      inline bool cmp(pll x,pll y){return x.first==y.first?x.second>y.second:x.first>y.first;}
      inline double col(int x,int y){
            return 1.0*(f[y]-f[x])/(1.0*(a[x+1].first-a[y+1].first));
      }
      void init(){
            N=read();
            up(i,1,N){
                  t[i].first=read();
                  t[i].second=read();
            }
            sort(t+1,t+N+1,cmp);
            ll last=0;
            t[0].first=0;t[0].second=0;
            up(i,1,N){
                  if(t[i].first<=t[last].first&&t[i].second<=t[last].second)continue;
                  else{
                        a[++cnt]=t[i];
                        last=i;
                  }
            }
            N=cnt;
      }
      void dp(){
            q[++tail]=0;
            up(i,1,N){
                  while(head<tail&&col(q[head],q[head+1])<=a[i].second)head++;
                  f[i]=f[q[head]]+a[q[head]+1].first*a[i].second;
                  while(head<tail&&col(q[tail],i)<=col(q[tail-1],q[tail]))tail--;
                  q[++tail]=i;
            }
      }
      void output(){
            cout<<f[N]<<endl;
      }
}
int main(){
      //freopen("input.in","r",stdin);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

DP斜率优化的套路貌似很固定的样子
 
提出决策相关的式子，然后各种变形，最后得出
(f(y)-f(x))/(s(y)-s(x))<p(i)之类的东西就行了
 
//OJ 1661
//by Cydiater
//2016.8.10
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <map>
#include <algorithm>
#include <ctime>
#include <cmath>
#include <cstring>
#include <string>
#include <iomanip>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
const int MAXN=1e6+5;
const int oo=0x3f3f3f3f;
inline ll read(){
      char ch=getchar();ll x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
ll N,A,B,C,sum[MAXN],q[MAXN],head,tail,f[MAXN];
namespace solution{
      inline double F(int x){return f[x]+A*sum[x]*sum[x]-B*sum[x];}
      inline double sqr(ll x){return x*x;}
      void init(){
            memset(sum,0,sizeof(sum));
            memset(f,0,sizeof(f));
            N=read();A=read();B=read();C=read();
            up(i,1,N)sum[i]=read()+sum[i-1];
      }
      void dp(){
            head=1;tail=0;q[++tail]=0;
            up(i,1,N){
                  while(head<tail&&F(q[head+1])-F(q[head])>sum[i]*2*A*(sum[q[head+1]]-sum[q[head]]))head++;
                  f[i]=f[q[head]]+A*(sum[i]-sum[q[head]])*(sum[i]-sum[q[head]])+B*(sum[i]-sum[q[head]])+C;
                  while(head<tail&&(F(i)-F(q[tail]))*(sum[q[tail]]-sum[q[tail-1]])>(F(q[tail])-F(q[tail-1]))*(sum[i]-sum[q[tail]]))tail--;
                  q[++tail]=i;
            }
      }
      void output(){
            cout<<f[N]<<endl;
      }
}
int main(){
      //freopen("input.in","r",stdin);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

BZOJ1096

又是一道鬼畜的斜率优化..
又是一如既往的推错公式
下面上公式编辑器
 
技术分享

技术分享

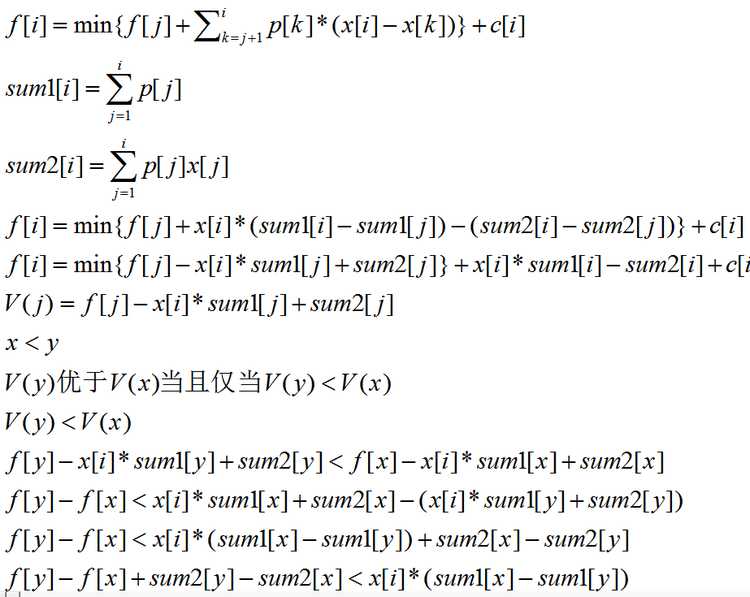
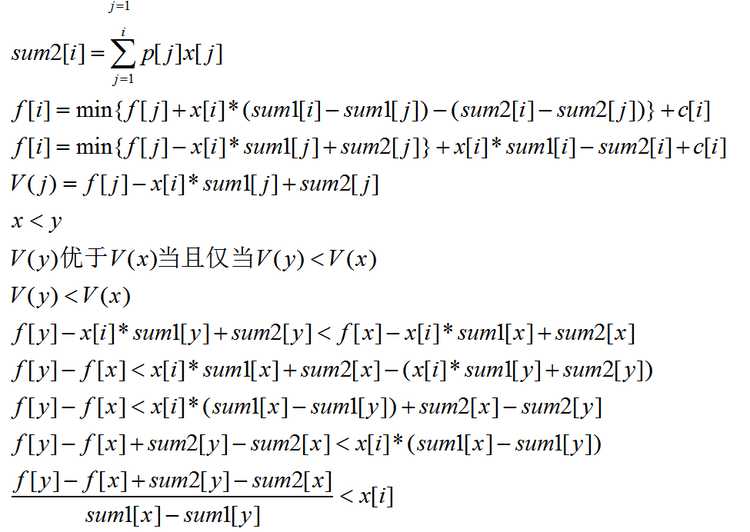
//OJ 1662
//by Cydiater
//2016.8.11
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <ctime>
#include <cmath>
#include <iomanip>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
const int MAXN=1e6+5;
const int oo=0x3f3f3f3f;
inline ll read(){
      char ch=getchar();ll x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
ll f[MAXN],p[MAXN],s[MAXN],cost[MAXN],N,q[MAXN],head,tail,sum1[MAXN],sum2[MAXN];
namespace solution{
      inline double col(int y,int x){
            double tmp1=f[x]-f[y]+sum1[x]-sum1[y];
            double tmp2=sum2[x]-sum2[y];
            return tmp1/tmp2;
      }
      void init(){
            N=read();
            up(i,1,N){
                  s[i]=read();
                  p[i]=read();
                  cost[i]=read();
                  sum1[i]=sum1[i-1]+p[i]*s[i];
                  sum2[i]=sum2[i-1]+p[i];
            }
      }
      void dp(){
            head=1;tail=0;q[++tail]=0;
            up(i,1,N){
                  while(head<tail&&col(q[head],q[head+1])<s[i])head++;
                  f[i]=cost[i]+s[i]*(sum2[i]-sum2[q[head]])-(sum1[i]-sum1[q[head]])+f[q[head]];
                  while(head<tail&&col(q[tail-1],q[tail])>col(q[tail],i))tail--;
                  q[++tail]=i;
            }
      }
      void output(){
            cout<<f[N]<<endl;
      }
}
int main(){
      freopen("input.in","r",stdin);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}
终于自己推出来一道题了
 
写完这道题豁然开朗了，之前很多不等式没推对一个很重要的原因就是
不等式右边应该是仅与i相关的多项式
不等式右边应该是仅与i相关的多项式
不等式右边应该是仅与i相关的多项式
 
重要的事情说三遍
下面给出推导：
 
技术分享

技术分享

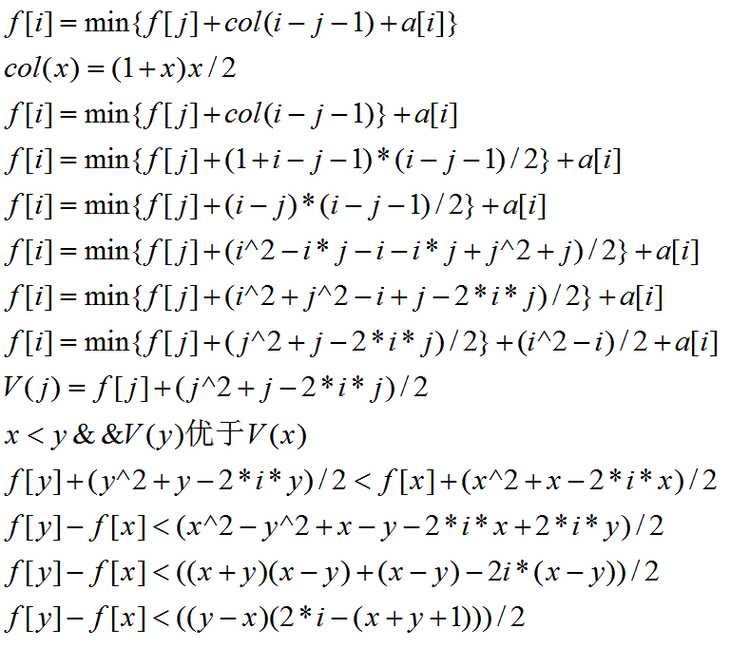
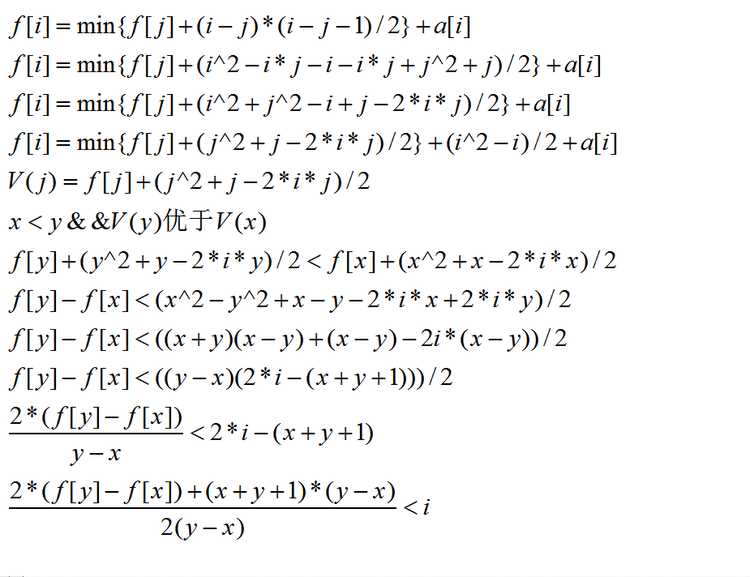
//BZOJ 3156
//by Cydiater
//2016.8.11
#include <iostream>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <ctime>
#include <cmath>
#include <cstdlib>
#include <iomanip>
#include <cstdio>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
const int MAXN=1e6+5;
const int oo=0x3f3f3f3f;
inline ll read(){
      char  ch=getchar();ll x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
ll N,f[MAXN],q[MAXN],head,tail,a[MAXN];
namespace solution{
      inline double col(ll x,ll y){
            double tmp1=2*(f[y]-f[x])+(x+y+1)*(y-x);
            double tmp2=2*(y-x);
            return tmp1/tmp2;
      }
      void init(){
            N=read();
            up(i,1,N)a[i]=read();
      }
      void dp(){
            head=1;tail=0;q[++tail]=0;
            up(i,1,N){
                  while(head<tail&&col(q[head],q[head+1])<i)head++;
                  f[i]=f[q[head]]+(i-q[head])*(i-q[head]-1)/2+a[i];
                  while(head<tail&&col(q[tail],i)<col(q[tail-1],q[tail]))tail--;
                  q[++tail]=i;
            }
      }
      void output(){
            printf("%lld\n",f[N]);
      }
}
int main(){
      //freopen("input.in","r",stdin);
      //freopen("out2.out","w",stdout);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

BZOJ 3675

因为这个会出现分母为0的情况..
所以应该把小于变成小于等于..
好坑..
 
技术分享 
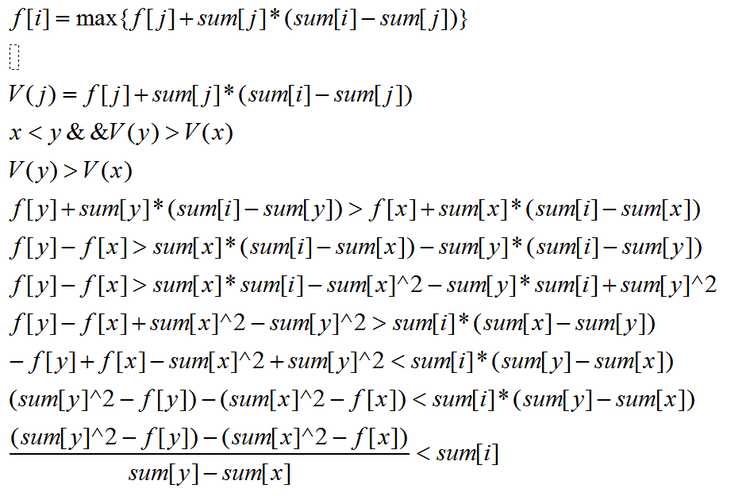
//BZOJ 3675
//by Cydiater
//2016.8.11
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>
#include <map>
#include <ctime>
#include <cmath>
#include <cstdlib>
#include <iomanip>
using namespace std;
#define ll long long
#define up(i,j,n)       for(int i=j;i<=n;i++)
#define down(i,j,n)     for(int i=j;i>=n;i--)
const int MAXN=1e5+5;
const int oo=0x3f3f3f3f;
inline ll read(){
      char  ch=getchar();ll x=0,f=1;
      while(ch>‘9‘||ch<‘0‘){if(ch==‘-‘)f=-1;ch=getchar();}
      while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();}
      return x*f;
}
ll N,K,sum[MAXN],f[MAXN][2],q[MAXN][2],head[205],tail[205];
namespace solution{
      inline ll col(int i,int k){return sum[k]*sum[k]-f[k][i];}
      inline bool judge(int x,int y,int z,int k){
            return (col(k,y)-col(k,x))*(sum[z]-sum[y])>=(col(k,z)-col(k,y))*(sum[y]-sum[x]);
      }
      void init(){
            N=read();K=read();K++;
            up(i,1,N)sum[i]=read()+sum[i-1];
      }
      void dp(){
            memset(f,0,sizeof(f));
            head[0]=1;tail[0]=0;q[++tail[0]][0]=0;
            up(j,1,K){
                  int k=j%2;
                  head[k%2]=1;tail[k%2]=0;
                  up(i,1,N){
                        while(head[k^1]<tail[k^1]&&col(k^1,q[head[k^1]+1][k^1])-col(k^1,q[head[k^1]][k^1])<sum[i]*(sum[q[head[k^1]+1][k^1]]-sum[q[head[k^1]][k^1]]))head[k^1]++;
                        f[i][k%2]=f[q[head[k^1]][k^1]][k^1]+sum[q[head[k^1]][k^1]]*(sum[i]-sum[q[head[k^1]][k^1]]);
                        while(head[k%2]<tail[k%2]&&judge(q[tail[k%2]-1][k%2],q[tail[k%2]][k%2],i,k%2))tail[k%2]--;
                        q[++tail[k%2]][k%2]=i;
                  }
            }
            /*up(i,1,K)up(j,1,N)
            printf("i==%d k==%d f[i][k]==%d\n",i,j,f[j][i]);*/
      }
      void output(){
            cout<<f[N][K%2]<<endl;
      }
}
int main(){
      //freopen("input.in","r",stdin);
      using namespace solution;
      init();
      dp();
      output();
      return 0;
}

 

 

优化DP的奇淫技巧

标签：

原文地址：http://www.cnblogs.com/Cydiater/p/5792782.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！