标签:
生成模型与判别模型
给定样本 $x$ ,需要对 $p(y|x)$ 建模,生成模型与判别模型分别使用了不同的方式
1. 生成模型
直接对 $p(x,y)$ 建模,通过贝叶斯公式得到 $y$ 的后验分布即可:
\[p(y|x) = \frac{p(x,y)}{p(x)}\]
生成模型反映了不同类型数据各自的特点,而且对后验概率建模,从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度,而不关心到底 decision boundary 在哪。最后找到 $y$ 值最大的即为 $x$ 对应的标记。
2. 判别模型
判别模型直接对 $p(y|x)$ 建模,或者学习决策函数 $y = f(x)$ ,目的是寻找不同类数据的决策平面.
生成 VS 判别:
典型的生成模型:B=NB,HMM,LDA,PLSA,GMM
典型的判别模型:LR, SVM, KNN, DT, MaxEnt,Boosting,CRF
有了
隐马尔科夫模型概述
隐马尔科夫模型 HMM 是用于标注问题的监督学习模型,属于一种生成模型,描述一个隐藏的马尔科夫链随机生成隐态序列,再由各个隐藏状态生成可观测序列的过程,如下图所示: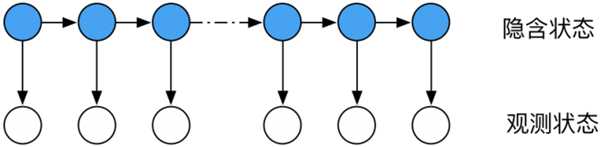
假设 Q 是所有可能的隐含状态集合, V 是所有可能的观测集合:
\[Q = \left \{q_1,q_2,…,q_N \right\}, \ \ V = \left \{v_1,v_2,…,v_M \right\}\]
H 是长度为 T 的隐态序列, O是对应的观测序列:
\[H = (h_1,h_2,…,h_T), \ \ O=(o_1,o_2,…,o_T)\]
A 是隐藏状态转移矩阵:
\[A = [a_{ij}]_{N \times N}\]
其中 A 中的每个元素代表当前时刻状态 为 q_i 下一时刻转到状态 q_j 的概率
\[a_{ij} = P(h_{i+1} = q_j | h_{t} = q_i)\]
B 是观测概率矩阵:
\[B = [b_j(k)]_{N \times M}\]
B 中的每个元素代表了在 t 时刻处于状态 q_j 的条件下生成观测态 v_k 的概率。
\[ b_j(k) = P(o_t = v_k = | h_t = q_j ) \]
\pi 是初始状态概率向量:
\[ \pi = \left \{ \pi_i \right \}_{i=1}^N , \ \ \pi_i = P(h_1 = q_i) \]
初始状态概率向量 \pi ,状态转移概率矩阵 A 与观测概率矩阵 B 共同构成了隐马尔科夫模型 \ lambda:
\[\lambda = \left \{A,B ,\pi \right \} \]
\pi 与 A 决定了隐马尔科夫链, B 决定了其观测态的生成, HMM 中的马尔科夫链是关于隐藏状态的链,模型有两个比较强基本假设:
齐次马尔科夫假设:马尔科夫链中在任意时刻 t 的隐态依赖于前一时刻的隐态,与观测态和当前时刻 t 无关:
\[P(h_t | h_{t-1},o_{t-1},…,h_1,o_1) = P(h_t|h_{t_1})\]
观测独立假设:任意时刻的观测状态只依赖于当前的隐态,与其他状态无关
\[P(o_t | h_T,o_T,…,h_1,o_1) = P(o_t|h_t)\]
HMM 的 3 个基本问题
概率计算问题:给定模型 $\lambda = \left \{A,B ,\pi \right \}$ ,和观测序列 $O=(o_1,o_2,…,o_T)$, 计算模型 $\lambda$ 中 O 出现的概率 $P(O|\lambda)$。
学习问题:已知观测序列 $O=(o_1,o_2,…,o_T)$, 估计模型参数 $ \lambda = \left \{A,B ,\pi \right \}$, 使得$P(O|\lambda)$ 在该模型下出现的概率最大, MLE 即可估计参数。
预测问题:给定模型 $ \lambda = \left \{A,B ,\pi \right \}$ 和预测序列 $O=(o_1,o_2,…,o_T)$ ,求给定观测序列的条件下最有可能的隐态序列 $H = (h_1,h_2,…,h_T)$ ,即对应的 $P(H|O)$ 最大的序列即可。
家下来分别解决这三个基本问题,首先是概率计算问题。
概率计算问题
给定模型 $\lambda = \left \{A,B ,\pi \right \}$ ,和观测序列 $O=(o_1,o_2,…,o_T)$,根据边缘概率与条件概率公式可得:
\[P(O|\lambda) = \sum_H P(H,O|\lambda) = \sum_H P(O|H,\lambda)P(H|\lambda)\]
只需枚举所有可能的状态序列然后求和即可得到最终的概率,但是该方法计算量非常大,是 $O(TN^T)$ 阶的,所以该方法只是理论上可行,但实际上式非常耗时的,一种有效的改进便是前后向算法(forward-backward algorithm),首先看前向概率,对于当前模型 \lambda ,定义到时刻 t 的观测序列为 $o_1,o_2,…,o_t$ ,且隐状为 q_i 的概率为前向概率,记做:
\[a_t(i) = P(o_1,o_2,…,o_t,h_t = q_i|\lambda)\]
前向概率可以递推求解,首先给定初值:
\[a_1(i) = \pi_ib_i(o_1)\]
这里 a_t(j) 是时刻 t 为观测序列为 $o_1,o_2,…,o_t$ 且在时刻 t 处于状态 q_j 的前向概率,那么 a_t(j)a_{ji} 则代表了在时刻 t 处于状态 q_j 而在 时刻 t+1 处于 q_i 的联合概率,对时刻 t 所有可能的 N 个状态求和 就是到时刻 t 观测为 $o_1,o_2,…,o_t$ 并在时刻 t 处于状态 q_j 且时刻 t+1 到达状态 q_i 的联合概率,最后乘以观测概率 b_i(o_{t+1}) 得到 a_{t+1}(i) 即可:
\[a_{t+1}(i) = \left \{ \sum_{j=1}^N a_t(j)a_{ji} \right \} b_i(o_{t+1}) \]
http://www.cnblogs.com/xiapeiyong/archive/2009/05/15/1457888.html
统计学习方法,PRML
http://freemind.pluskid.org/machine-learning/discriminative-modeling-vs-generative-modeling/
标签:
原文地址:http://www.cnblogs.com/ooon/p/5792774.html