标签:
T1
Description
小W和小M一起玩拼图游戏啦~
小M给小M一张N个点的图,有M条可选无向边,每条边有一个甜蜜值,小W要选K条边,使得任意两点间最多有一条路径,并且选择的K条边甜蜜值之和最大。
Input
第一行三个正整数N,M,K。
接下来M行,每行三个正整数A,B,C表示A、B两点间有一条甜蜜值为C的无向边。
Output
一行输出最大甜蜜值之和。
Sample Input
5 4 3
1 2 10
1 3 9
2 3 7
4 5 3
Sample Output
22
HINT
N,M<=100000
Solution
kruskal裸题(听说某位wwd巨神直接写了kruskal交上去,然后WA了,因为他没看到K)。
#include<cmath> #include<ctime> #include<stack> #include<queue> #include<cstdio> #include<vector> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define N 100005 using namespace std; struct edge{ int l,r,w; }a[N]; int f[N],n,m,k,ans; inline int read(){ int ret=0;char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)){ ret=ret*10+c-‘0‘; c=getchar(); } return ret; } inline bool cmp(edge x,edge y){ return x.w>y.w; } inline int gf(int k){ if(f[k]==k) return k; return f[k]=gf(f[k]); } inline void init(){ n=read();m=read();k=read(); for(int i=1;i<=m;i++){ a[i].l=read();a[i].r=read(); a[i].w=read();f[i]=i; } sort(a+1,a+1+m,cmp); for(int i=1,p,q;k&&i<=m;i++){ p=gf(a[i].l);q=gf(a[i].r); if(p!=q){ k--;ans+=a[i].w;f[p]=q; } } printf("%d\n",ans); } int main(){ freopen("carpet.in","r",stdin); freopen("carpet.out","w",stdout); init(); fclose(stdin); fclose(stdout); return 0; }
T2
Description
小W顺利地完成了拼图,该他给小M出题啦。
小W定义“!”运算符:
1.N!k=N!(k-1)*(N-1)!k (N>0且k>0)
2.N!k=1 (N=0)
3.N!k=N (k=0)
现在小W告诉小M N和k,小M需要说出N!k的不同约数个数。
为了降低难度,答案对1000000009取模就好了。
Input
第一行两个整数 N,M。
Output
一行一个整数,为答案。
Sample Input
3 1
Sample Output
4
HINT
N<=1000,k<=100
Solution
解法一:
质因数分解一个数x为x=p1a1p2a2……pkak(pi为不同的质数)
则x的不同约数个数为(a1+1)(a2+1)……(ak+1)。
所以只需知道N!K的约数个数即可。
设f[i][j][k]为i!j的结果中,第k个质数的个数:
f[i][j][k]=f[i][j-1][k]+f[i-1][j][k](i>0且j>0)
f[i][j][k]=0(i=0)
f[i][j][k]=N分解质因数后的结果(j=0)
解法二:
随便推推会发现和杨辉三角形很像,然后就很容易做了。
#include<cmath> #include<ctime> #include<stack> #include<queue> #include<cstdio> #include<vector> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define P 170 #define K 101 #define N 1001 #define M 1000000009 #define MOD 1000000009ll using namespace std; typedef long long ll; struct total{ int t[P]; }f[N][K]; ll ans; int p[P],n,k,cnt; bool b[N]; inline void prime(){ for(int i=2;i<N;i++){ if(!b[i]) p[++cnt]=i; for(int j=1;j<=cnt&&p[j]*i<N;j++){ b[p[j]*i]=true; if(!(i%p[j])) break; } } } inline total add(total a,total b){ for(int i=1;i<P;i++) a.t[i]=(a.t[i]+b.t[i])%M; return a; } inline void init(){ scanf("%d%d",&n,&k); if(n<0||k<0) return; prime(); for(int i=1,x;i<=n;i++){ x=i; for(int j=1;x&&j<=cnt;j++) while(x&&!(x%p[j])){ x/=p[j]; if(++f[i][0].t[j]==M) f[i][0].t[j]=0; } } for(int i=1;i<=n;i++) for(int j=1;j<=k;j++) f[i][j]=add(f[i-1][j],f[i][j-1]); ans=1; for(int i=1;i<=cnt;i++) ans=ans*(ll)(f[n][k].t[i]+1)%MOD; printf("%lld\n",ans); } int main(){ freopen("calc.in","r",stdin); freopen("calc.out","w",stdout); init(); fclose(stdin); fclose(stdout); return 0; }
T3
Description
小W和小M正在出国旅游中~
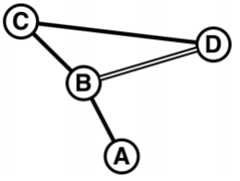
他们到的国家共有n个城市,由m条分别属于c家公司的双向路连接。
上图是路线图的一个例子。假设要从车站A到车站D,最短的路线显然是A→B→D。
然而,最短的路线并不意味着最便宜的路线。上图中,铁路A?B,B?C,C?D属于同一家铁路公司,而铁路B?D属于另一家铁路公司,那么此时路线A→B→C→D就可能比路线A→B→D便宜。
这其中的主要原因,就是连续一段属于同一家铁路公司的路线花费并不与长度成正比,通常长度越长单位长度的花费就越少。那么,最终的路线可以被分为若干段,每段都属于同一家铁路公司,总花费就是每段花费之和。
Input
第一行5个整数,分别表示n,m,c,s,t。
接下来m行,每行4个整数xi,yi,zi,bi,表示在车站xi与yi之间,长度为zi。
接下来1行c个整数pi,表示第i家铁路公司的收费表有pi段。
接下来2c行,每两行为一组,表示第i家公司的收费标准:
第一行pi-1个整数qi,j;
第二行pi个整数ri,j;
fi(x)=fi(x-1)+ri,j (qi,j-1<x<=qi,j,1<=j<=pi),
其中fi(0)=0,qi,0=0,qi,pi=∞,qi,j随j递增,ri,j随j递减。
如果您看过原题的输入说明的话,您一定会觉得简写的我很良心。
Output
若存在从s到t的路线,则第一行包含一个整数,表示最小花费;否则第一行包含一个整数?1。
Sample Input
4 4 2 1 4
1 2 2 1
2 3 2 1
3 4 5 1
2 4 4 2
3 2
3 6
10 5 3
100
10 9
Sample Output
54
HINT
2<=n<=100,0<=m<=104,1<=c<=20,s≠t,xi≠yi,1<=zi<=200,
1<=pj<=50,1<=qj,k<=104,1<=rj,k<=100
Solution
floyd预处理出只走第i家铁路公司的最低费用dis[i][][],floyd求最短路就是答案。
#include<cmath> #include<ctime> #include<cstdio> #include<vector> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define C 25 #define P 55 #define N 105 #define M 20005 #define INF 2000000 using namespace std; int q[C][P],r[C][P],p[C]; int a[C][N][N],dis[N][N],n,m,c,s,t; inline int cost(int len,int t){ int c=0; for(int i=1;i<p[t];i++) if(len<=q[t][i]){ c+=(len-q[t][i-1])*r[t][i];break; } else c+=(q[t][i]-q[t][i-1])*r[t][i]; if(len>q[t][p[t]-1]) c+=(len-q[t][p[t]-1])*r[t][p[t]]; return c; } inline void floyd1(){ int d[N][N]; for(int l=1;l<=c;l++){ for(int i=1;i<n;i++) for(int j=i+1;j<=n;j++) d[i][j]=d[j][i]=a[l][i][j]; for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) d[j][i]=d[i][j]=min(d[i][j],d[i][k]+d[j][k]); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(d[i][j]!=INF) dis[i][j]=min(dis[i][j],cost(d[i][j],l)); } } inline void floyd2(){ for(int k=1;k<=n;k++) for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dis[i][j]=dis[j][i]=min(dis[i][j],dis[i][k]+dis[j][k]); } inline void init(){ scanf("%d%d%d%d%d",&n,&m,&c,&s,&t); for(int i=1;i<n;i++) for(int j=i+1;j<=n;j++){ dis[j][i]=dis[i][j]=INF; for(int k=1;k<=c;k++) a[k][i][j]=a[k][j][i]=INF; } for(int i=1,j,k,l,w;i<=m;i++){ scanf("%d%d%d%d",&j,&k,&w,&l); a[l][j][k]=a[l][k][j]=min(a[l][j][k],w); } for(int i=1;i<=c;i++) scanf("%d",&p[i]); for(int i=1;i<=c;i++){ for(int j=1;j<p[i];j++) scanf("%d",&q[i][j]); for(int j=1;j<=p[i];j++) scanf("%d",&r[i][j]); } floyd1();floyd2(); if(dis[s][t]==INF) printf("-1\n"); else printf("%d\n",dis[s][t]); } int main(){ freopen("railway.in","r",stdin); freopen("railway.out","w",stdout); init(); fclose(stdin); fclose(stdout); return 0; }
为何这次又不简化题面?因为后面几天的题小W和小M都在虐狗QAQ
标签:
原文地址:http://www.cnblogs.com/AireenYe/p/5793047.html