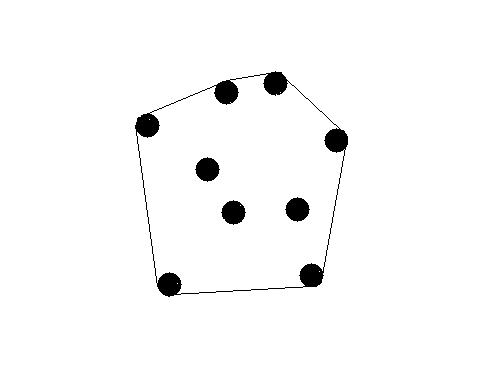
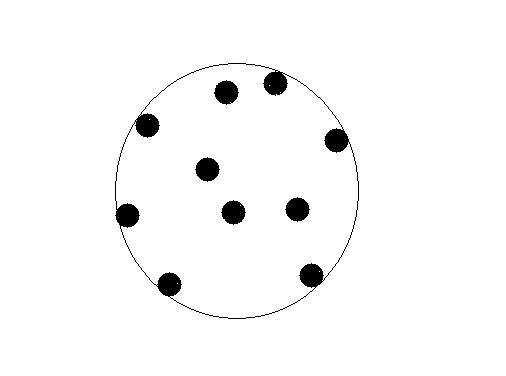
1 #include<stdio.h>
  2 #include<math.h>
  3 #define PI acos(-1.0)
  4 struct   TPoint
  5 {
  6     double x,y;
  7 }a[1005],d;
  8 double r;
  9 double   distance(TPoint   p1,   TPoint   p2)
 10 {
 11     return (sqrt((p1.x-p2.x)*(p1.x -p2.x)+(p1.y-p2.y)*(p1.y-p2.y)));
 12 }
 13 double multiply(TPoint   p1,   TPoint   p2,   TPoint   p0)
 14 {
 15     return   ((p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y));
 16 }
 17 void MiniDiscWith2Point(TPoint   p,TPoint   q,int   n)
 18 {
 19     d.x=(p.x+q.x)/2.0;
 20     d.y=(p.y+q.y)/2.0;
 21     r=distance(p,q)/2;
 22     int k;
 23     double c1,c2,t1,t2,t3;
 24     for(k=1; k<=n; k++)
 25     {
 26         if(distance(d,a[k])<=r)
 27             continue;
 28         if(multiply(p,q,a[k])!=0.0)
 29         {
 30             c1=(p.x*p.x+p.y*p.y-q.x*q.x-q.y*q.y)/2.0;
 31             c2=(p.x*p.x+p.y*p.y-a[k].x*a[k].x-a[k].y*a[k].y)/2.0;
 32 
 33             d.x=(c1*(p.y-a[k].y)-c2*(p.y-q.y))/((p.x-q.x)*(p.y-a[k].y)-(p.x-a[k].x)*(p.y-q.y));
 34             d.y=(c1*(p.x-a[k].x)-c2*(p.x-q.x))/((p.y-q.y)*(p.x-a[k].x)-(p.y-a[k].y)*(p.x-q.x));
 35             r=distance(d,a[k]);
 36         }
 37         else
 38         {
 39             t1=distance(p,q);
 40             t2=distance(q,a[k]);
 41             t3=distance(p,a[k]);
 42             if(t1>=t2&&t1>=t3)
 43             {
 44                 d.x=(p.x+q.x)/2.0;
 45                 d.y=(p.y+q.y)/2.0;
 46                 r=distance(p,q)/2.0;
 47             }
 48             else if(t2>=t1&&t2>=t3)
 49             {
 50                 d.x=(a[k].x+q.x)/2.0;
 51                 d.y=(a[k].y+q.y)/2.0;
 52                 r=distance(a[k],q)/2.0;
 53             }
 54             else
 55             {
 56                 d.x=(a[k].x+p.x)/2.0;
 57                 d.y=(a[k].y+p.y)/2.0;
 58                 r=distance(a[k],p)/2.0;
 59             }
 60         }
 61     }
 62 }
 63 
 64 void MiniDiscWithPoint(TPoint   pi,int   n)
 65 {
 66     d.x=(pi.x+a[1].x)/2.0;
 67     d.y=(pi.y+a[1].y)/2.0;
 68     r=distance(pi,a[1])/2.0;
 69     int j;
 70     for(j=2; j<=n; j++)
 71     {
 72         if(distance(d,a[j])<=r)
 73             continue;
 74         else
 75         {
 76             MiniDiscWith2Point(pi,a[j],j-1);
 77         }
 78     }
 79 }
 80 int main()
 81 {
 82     int i,n;
 83     while(scanf("%d",&n)&&n)
 84     {
 85         for(i=1; i<=n; i++)
 86             scanf("%lf %lf",&a[i].x,&a[i].y);
 87         if(n==1)
 88         {
 89             printf("0.50\n");
 90             continue;
 91         }
 92 
 93         r=distance(a[1],a[2])/2.0;
 94         d.x=(a[1].x+a[2].x)/2.0;
 95         d.y=(a[1].y+a[2].y)/2.0;
 96         for(i=3; i<=n; i++)
 97         {
 98             if(distance(d,a[i])<=r)
 99                 continue;
100             else
101                 MiniDiscWithPoint(a[i],i-1);
102         }
103         printf("%.2lf\n",r+0.5);
104     }
105     return 0;
106 }