标签：
第3张 探索数据
第2章讨论知识发现过程中重要的高层数据问题。本章是数据探索，对数据进行初步研究，以便更好地理解它的特殊性质。数据探索有助于选择合适的数据预处理和数据分析技术。甚至可以处理一些通常由数据挖掘解决的问题。例如，有时可以通过对数据进行直观检查来发现模式。
本章包括三个主题：汇总统计、可视化和联机分析处理OLAP。汇总统计（如值集合的均值和标准差）和可视化技术是广泛用于数据探索的标准方法。OLAP的分析功能集中在从多为数据数组中创建汇总表的各种方法。OLAP技术包括在不同的维上或不同的属性值上聚集数据，例如，如果给定基于产品、位置和日期记录的销售信息，则可以使用OLAP技术创建按月和按产品类别描述特定地点的销售活动汇总。
本章涵盖的主题与探讨性数据分析（Exploratory Data Analysis,EDA）有许多重叠。本章特别强调可视化。
3.1 鸢尾花数据集
经常提到鸢尾花Iris数据集，鸢尾花数据集包含150种鸢尾花的信息，每50种取自三个鸢尾花种之一：Setosa、Versicolour和Virginica。每个花的特征用下面5种属性描述。
（1）萼片长度
（2）萼片宽度
（3）花瓣长度
（4）花瓣宽度
（5）类
花的萼片是花的外部结构，保护花的更脆弱的部分。许多花中，萼片是绿色的，只有花瓣是鲜艳多彩的。而对于鸢尾花，萼片也是鲜艳多彩的。鸢尾花的萼片比花瓣大并且下垂，而花瓣向上。
3.2 汇总统计
汇总统计（summary statistics）是量化的（如均值和标准差），用单个数或数的小集合捕获可能很大的值集的各种特征。我们将集中讨论对单个属性值的汇总统计，但是也将简略介绍某些多元汇总统计。
本节只考虑汇总统计的描述性质。
3.2.1 频率和众数
给定一个无序的、分类的值的集合，为进一步刻画值得性质，除计算特定数据集中每个值出现的频率外没有多少的事情可做。给定一个在{v1,v2,...,vk}上取值的分类属性x和m个对象的集合，值vi的频率定义为：
分类属性的众数（mode）是具有最高频率的值。分类属性常常具有少量值，因此这些值得众数和频率可能是令人感兴趣的和有用的。尽管如此，对于鸢尾花数据集和类属性，由于三种类型的花具有相同的频率，因此众数的改变并无意义。
对于连续数据，按照目前的定义，众数通常没有用，因为单个值得出现可能不超过一次，然而，某些情况下，众数可能提供关于值得性质或关于出现遗漏值得重要信息。
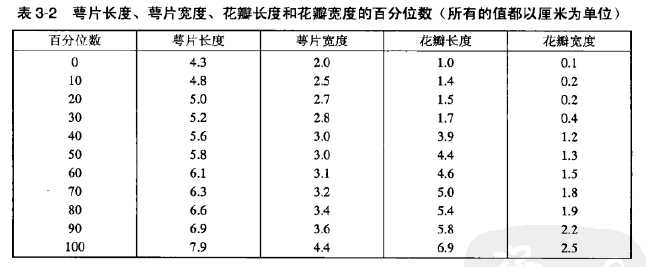
3.2.2 百分位数
对于有序数据，考虑值集的百分位数（percentile）更有意义。具体的说，给定一个有序的或连续的属性x和0到100之间的数p，第p个百分位数Xp是一个x值，使得x的p%的观测值小于Xp。
3.2.3 位置度量：均值和中位数
对于连续数据，两个使用最广泛的汇总统计是均值（mean）和中位数（median），它们是值集的位置度量。考虑m个对象的集合和属性x，设{x1,x2,...,xm}是这m个对象的x属性值。设{x‘1,x‘2,...,x‘m}代表以非递减排序后的x值，这样x‘1=min(x),x‘m=max(x)，于是均值和中位数的定义如下：
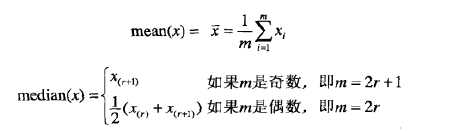
如果值得分布是倾斜的，则中位数是中间的一个更好的指示符。此外，均值对于离群值很敏感：对于包含离群值的数据，中位数可以再次更稳健地提供值集中间的估计。
为了克服传统均值定义的问题，有时使用截断均值概念。制定0和100之间的百分位数p，丢弃高端和低端(p/2)%的数据，然后用常规的方法计算均值，所得的结果既是截断均值。
3.2.4 散步度量：极差和方法
连续数据的另一组常用的汇总统计是值集的弥散或散布度量。这种度量表明属性值是否散布很宽，或者是否相对集中在单个点附近。
最简单的散布度量是极差（range）。给定属性x，它具有m个值{x1,....,xm}，x的极差定义为：
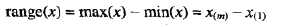
尽管极差标识最大散布，但是如果大部分值都集中在一个较窄的范围内，并且更极端的值得个数相对较少，则可能会引起误解。因此，作为散布的度量，方差更可取。通常，属性x的值得方差记作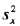
，并在下面定义。标准差（standard deviation）是方差的平方根，记作Sx，它与x具有相同的单位：
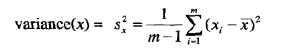
均值可能被离群值扭曲，并且由于方差用均值计算，因此它也对离群值敏感。确实，方差对离群值特别敏感，因为它使用均值与其他值的差的平方，这样常常需要使用比值集散布更稳健的估计。下面是三种这样的度量的定义：绝对平均偏差（AAD）、中位数绝对偏差（MAD）和四分位数极差（IQR）。
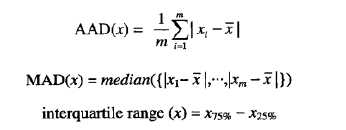
3.2.5 多元汇总统计
包含多个属性的数据（多元数据）的位置度量可以通过分别计算每个属性的均值或中位数得到。这样，给定一个数据集，数据对象的均值由：
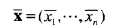
对于多元数据，每个属性的散布可以独立于其他属性。然而，对于具有连续变量的数据，数据的散布更多地用协方差矩阵（Convariance matrix）S表示，其中
两个属性的协方差是两个属性一起变化并依赖于变量大小的度量。协方差的值接近于0表明两个变量不具有关系，但是不能仅靠观察协方差的值来确定两个变量之间的关联程度。因为两个属性的相关性直接指出两个属性相关的程度，对于数据探索，相关性比协方差更可取。
3.2.6 汇总数据的其他方法
例如，值集的倾斜度度量值对称地分布在均值附近的程度。许多情况下，理解关于属性值如何分布的更复杂、更微妙的方面，最有效的方法是通过直方图观察这些值。
3.3 可视化
成功的数据可视化需要将数据转换成可视的形式，以便能够借此分析或报告数据的特征和数据项或属性之间的关系。可视化的目标是形成可视化信息的人工解释和信息的意境模型。
可视化技术常常是有限选择的方法。尽管在数据挖掘中通常强调算法或数学方法，但是可视化技术也能在数据分析方面起关键作用。事实上，有时将可视化技术在数据挖掘方面的应用称作可视化数据挖掘（visual data mining）。
3.3.1 可视化的动机
使用可视化技术的首要动机是人们能够快速地吸取大量可视化信息，并发现其中的模式。
3.3.2 一般概念
1. 表示：将数据映射到图形元素
可视化的第一步就是讲信息映射成可视形式，即将信息中的对象、属性和联系映射成可视的对象、属性和联系。
2. 安排
正确选择对象和属性的可视化表示是基本的要求。
3. 选择
可视化的另一个关键概念是选择（selection），即删除或不突出某些对象和属性。具体来说，尽管只具有少数维的数据对象通常可以使用直截了当的方法映射成二维或三维图形表示，但是没有令人完全满意和一般的方法表示具有许多属性的数据。同样，如果有很多数据对象，则可视化所有的对象可能导致显示过于拥挤。如果有许多属性和许多对象，则情况会更复杂。
如果维度不太高，则可以构造双变量图矩阵用于联合观察。选择一堆属性的技术是一类维归约，并且有许多更复杂的维归约可以使用，如主成分分析（PCA）。
3.3.3 技术
1. 少量属性的可视化
茎叶图、直方图、二维直方图、盒状图、饼图、散布图、
2. 可视化时间空间数据
等高线图、曲面图、矢量场图
3.3.4 可视化高维数据
矩阵、平行坐标系、
《数据挖掘导论》 - 读书笔记(4) - 探索数据 [2016-8-20]
标签：
原文地址：http://www.cnblogs.com/pythonMLer/p/5791110.html
