【POJ 1487】Single-Player Games（建方程高消）

Single-Player Games Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 1387 Accepted: 377 Description Playing games is the most fun if other people take part. But other players are not always available if you need them, which led to the invention of single-player games. One of the most well-known examples is the infamous Solitaire‘‘ packaged with Windows, probably responsible for more wasted hours in offices around the world than any other game. <br>The goal of a single-player game is usually to makemoves” until one reaches a final state of the game, which results in a win or loss, or a score assigned to that final state. Most players try to optimize the result of the game by employing good strategies. In this problem we are interested in what happens if one plays randomly. After all, these games are mostly used to waste time, and playing randomly achieves this goal as well as any other strategy. Games can very compactly represented as (possibly infinite) trees. Every node of the tree repre- sents a possible game state. The root of the tree corresponds to the starting position of the game. For an inner node, its children are the game states to which one can move in a single move. The leaf nodes are the final states, and every one of them is assigned a number, which is the score one receives when ending up at that leaf. 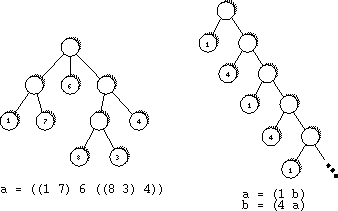Trees are defined using the following grammar. Definition ::= Identifier “=” RealTree RealTree ::= “(“Tree+“)” Tree ::= Identifier | Integer | “(“Tree+“)” Identifier ::= a|b|…|z Integer ∈ {…,-3,-2,-1,0,1,2,3,…,} By using a Definition, the RealTree on the right-hand side of the equation is assigned to the Identifier on the left. A RealTree consists of a root node and one or more children, given as a sequence enclosed in brackets. And a Tree is either . the tree represented by a given Identifier, or . a leaf node, represented by a single Integer, or . an inner node, represented by a sequence of one or more Trees (its children), enclosed in brackets. Your goal is to compute the expected score, if one plays randomly, i.e. at each inner node selects one of the children uniformly at random. This expected score is well-defined even for the infinite trees definable in our framework as long as the probability that the game ends (playing randomly) is 1. Input The input file contains several gametree descriptions. Each description starts with a line containing the number n of identifiers used in the description. The identifiers used will be the first n lowercase letters of the alphabet. The following n lines contain the definitions of these identifiers (in the order a, b, …). Each definition may contain arbitrary whitespace (but of course there will be no spaces within a single integer). The right hand side of a definition will contain only identifiers from the first n lowercase letters. The inputs ends with a test case starting with n = 0. This test case should not be processed. Output For each gametree description in the input, first output the number of the game. Then, for all n identifiers in the order a, b, …, output the following. If an identifier represents a gametree for which the probability of finishing the game is 1, print the expected score (when playing randomly). This value should be exact to three digits to the right of the decimal point. If the game described by the variable does not end with probability 1, print “Expected score of id undefined” instead. Output a blank line after each test case. Sample Input 1 a = ((1 7) 6 ((8 3) 4)) 2 a = (1 b) b = (4 a) 1 a = (a a a) 0 Sample Output Game 1 Expected score for a = 4.917 Game 2 Expected score for a = 2.000 Expected score for b = 3.000 Game 3 Expected score for a undefined Source Southwestern European Regional Contest 1998

找了一下午BUG，头一遭做Gauss做到想吐……
刷其他类型的题也没有过这么折腾人……现在胃里还翻江倒浪的……

做不出来不算最难受的，最难受的是不断找bug不断wa……

首先这题给出的是n个树。
每个节点表示一种状态。
已知从每个点到后面任何一种状态的概率相同。
一些状态标有权值，并且是叶子，到达这种状态游戏结束，同时获得节点上的权值。
问从n种状态出发，各自的期望。

起初考虑建方程考虑了许久。

画来画去，往类似树dp那种思想上靠，结果想出来了。

类似
a = (b (c 2))
b = (c (b 3))
c = (b 4)
其实就可以列三个方程
$x_a = \frac{1}{2} x_b + \frac{1}{4} x_b + \frac{1}{4}\cdot2$
$x_b = \frac{1}{2} x_c + \frac{1}{4} x_b + \frac{1}{4}\cdot3$
$x_c = \frac{1}{2} x_b + \frac{1}{2}\cdot4$

发现了么，移一下项就变成了多元方程组了！

然后套一个double的Gauss
然后就开始Debug之旅了……

首先是建方程的dfs函数
1* 要注意处理空格、数字、字母，要非常小心！
2* 高斯消元找到当前行k后，化简后几行时，要用第i行减第k行化简的结果。
即$a[i][j] -= a[k][j]*(a[k][col]/a[i][col)$
而不是 $a[i][j] = a[i][j]*(a[i][col]/a[k][col])-a[k][j]$
后一种会导致精度爆炸！
3* 可能会有多解，对于多解，要遍历每一个方程，如果当前方程内系数非0的只有一个变元，那么可以求出其值，否则无穷解。
4* 注意输出，是要输出每一种元素的结果，不要被第三组迷惑！（也可能傻的只有我一人……以为存在多解就全部那么输出……
5* 细节……

代码如下：

#include <iostream>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <climits>
#include <ctime>
#include <cstring>
#include <queue>
#include <stack>
#include <list>
#include <algorithm>
#include <map>
#include <set>
#define LL long long
#define Pr pair<int,int>
#define fread(ch) freopen(ch,"r",stdin)
#define fwrite(ch) freopen(ch,"w",stdout)

using namespace std;
const int INF = 0x3f3f3f3f;
const int msz = 10000;
const int mod = 1e9+7;
const double eps = 1e-6;
const int MAXN=33;
double a[MAXN][MAXN],x[MAXN];
int free_x[MAXN];
int equ,var;

int Gauss()
{

    int i,j,k,col,max_r;
    memset(free_x,0,sizeof(free_x));
    for(k=0,col=0;k<equ&&col<var;k++,col++)
    {
        max_r=k;
        for(i=k+1;i<equ;i++)
            if(fabs(a[i][col])>fabs(a[max_r][col])) max_r=i;

        if(fabs(a[max_r][col]) < eps)
        {
            k--;
            continue;
        }

        if(k!=max_r)
            for(j=col;j<=var;j++) swap(a[k][j],a[max_r][j]);

        for(int i = k+1; i < equ; ++i)
        {
            if(fabs(a[i][col]) <= eps) continue;
            for(int j = col+1; j <= var; ++j)
                a[i][j] = a[i][j]-a[i][col]/a[k][col]*a[k][j];

            a[i][col] = 0;
        }
    }

    for(int i = k; i < equ; ++i)
        if(fabs(a[i][var]) >= eps) return -1;

    if(k < equ)
    {
        for(int i = k-1; i >= 0; --i)
        {
            int id,cnt = 0;
            for(int j = 0; j < var; ++j)
            {
                if(fabs(a[i][j]) <= eps) continue;
                if(free_x[j]) continue;
                cnt++;
                id = j;
            }
            if(cnt > 1) continue;

            double tmp = a[i][var];

            for(int j = var-1; j >= 0; --j)
            {
                if(fabs(a[i][j]) > eps && j != id) tmp -= a[i][j]*x[j];
            }

            x[id] = tmp/a[i][id];
            free_x[id] = 1;
        }

        return equ-k;
    }

    for(int i = equ-1; i >= 0; --i)
    {
        double tmp = a[i][var];

        for(int j = var-1; j > i; --j)
        {
            tmp -= a[i][j]*x[j];
        }

        x[i] = tmp/a[i][i];
    }

    return 0;
}

char str[2333];

void dfs(int pos,int l,int r,double x)
{
    int per = 0;
    int pi = 0;

    bool f = 1;
    for(int i = l; i <= r; ++i)
    {
        if(str[i] == ‘ ‘) continue;
        per++;
        if(str[i] == ‘(‘)
        {
            f = 0;
            ++i;
            pi = 1;
            while(pi)
            {
                if(str[i] == ‘(‘) pi++;
                else if(str[i] == ‘)‘) pi--;
                ++i;
            }
        }
        else while(str[i] != ‘ ‘ && str[i] != ‘(‘ && str[i] != ‘)‘ && i <= r) ++i;
        --i;
    }
    x /= per;
    int st,en;

    if(f && per == 1)
    {
        for(int i = l; i <= r; ++i)
        {
            if(‘a‘ <= str[i] && str[i] <= ‘z‘)
            {
                a[pos][str[i]-‘a‘] -= x;
                return;
            }
        }

        int tmp;
        sscanf(str+l,"%d",&tmp);
        a[pos][var] += x*tmp;
        return;
    }

    for(int i = l; i <= r; ++i)
    {
        if(str[i] == ‘ ‘) continue;
        st = i;

        if(str[i] == ‘(‘)
        {
            ++i;
            pi = 1;
            while(pi)
            {
                if(str[i] == ‘(‘) pi++;
                else if(str[i] == ‘)‘) pi--;
                ++i;
            }
            dfs(pos,st+1,i-2,x);
        }
        else 
        {
            while(str[i] != ‘ ‘ && str[i] != ‘(‘ && str[i] != ‘)‘ && i <= r) ++i;
            dfs(pos,st,i-1,x);
        }
        --i;
    }
}

void init(int n)
{
    equ = var = n;
    memset(a,0,sizeof(a));

    for(int i = 0; i < n; ++i)
    {
        gets(str);

        int pos = 0;
        a[str[pos]-‘a‘][str[pos]-‘a‘] = 1;
        pos++;
        while(str[pos] == ‘ ‘ || str[pos] == ‘=‘) pos++;
        dfs(i,pos,strlen(str)-1,1);
    }
}

int main()
{
    //fread("in.in");
    //fwrite("my.out");

    int n,z = 1;

    while(~scanf("%d",&n) && n)
    {
        getchar();
        init(n);

        int t = Gauss();

        printf("Game %d\n",z++);
        for(int i = 0; i < n; ++i) 
        {
            printf("Expected score for %c ",‘a‘+i);
            if(t == -1 || (t && !free_x[i])) puts("undefined");
            else printf("= %.3f\n",x[i]);
        }

        puts("");
    }

    return 0;
}