标签:
Given two strings, find the longest common subsequence (LCS). 最长公共子序列
Your code should return the length of LCS.
What‘s the definition of Longest Common Subsequence?
For "ABCD" and "EDCA", the LCS is "A" (or "D", "C"), return 1.
For "ABCD" and "EACB", the LCS is "AC", return 2.
应用: 在生物工程中,比较两个DNA串的相似性。
解题:
1. 首先,必须弄清楚什么是子序列,什么是最长公共子序列;
2. 容易想的方法就是暴力求解,穷举所有子序列,然后找到最大的,然而这种指数级别的复杂度肯定不合适。
3. 所以我们需要分析问题,刻画公共子序列所具有的特征;
假设: 有两个字符串 A = “ABCDUHNEK” ; B = ”KFACEKLO“ ;求解他两的最大公共子序列;
首先:两个字符串的长度设为: m=A.length(), n=B.length();
我们考虑两个字符串的最后一个字符A[m-1] 和 B[n-1] 。
(1)假如相等:两个字符串的最长公共子序列就一定包含最后一个字符,而且它的长度应该等价于字符串 A‘ = “ABCDUHNE” 与 B’ = ”KFACEKL“ 的最大公共子序列的长度+1;
(2)假如不相等:两个字符串的最长公共子序列就有两种情况:等价于,A = “ABCDUHNEK” 与 B‘ = ”KFACEKL“ 的最大公子序列长度 或者
A‘ = “ABCDUHNE” 与 B = ”KFACEKLO“ 的最大公共子序列长度。
有此特点可以得到这个问题的递归解公式:
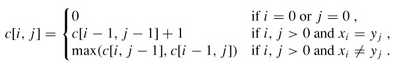
其中c[i,j]定义为一个二维数组,用于存储两个字符串最长公共子序列的长度。下标i,j表示字符串A中的前i-1个字符和 字符串B中的前 j-1个字符所具有的最长公共子串(注意:数组计数从0开始)。
递归求解,可得类似下表:
X字符串:ABCBDAB
Y字符串:BDCABA
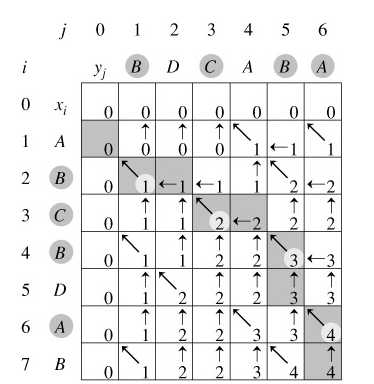
算法时间复杂度为:Θ(m + n)。
实现代码如下:
class Solution { public: /** * @param A, B: Two strings. * @return: The length of longest common subsequence of A and B. */ int longestCommonSubsequence(string A, string B) { // write your code here //最大公共子序列,方法在算法导论中有专门讲解。当学完之后来看,题目很简单。 //编程习惯要好! 注意括号对称,循环嵌套缩进!!! int a=A.size();//两个字符串的长度 int b=B.size(); int num; //最大公共子序列长度 int c[a+1][b+1];//定义二维数组,用来存放最大公共子序列的长度,注意定义和引用时下标的区别; for(int i=0;i<a+1;i++){ c[i][0]=0; } for(int j=1;j<b+1;j++){ c[0][j]=0; } for(int i=0;i<a;i++){ for(int j=0;j<b;j++){ if(A[i]==B[j]){ c[i+1][j+1]=c[i][j]+1; } else{ if(c[i][j+1]>=c[i+1][j]){ c[i+1][j+1]=c[i][j+1]; } else{ c[i+1][j+1]=c[i+1][j]; } } } } num=c[a][b]; return num; } };
附:当需要返回最长公共子序列时,只需要在上面所考虑的三中情况下都设置相应的标记位就能实现了。表格中所画的三种箭头,在实际实现时可以用0,1,-1三个标志位来表示。
标签:
原文地址:http://www.cnblogs.com/Allen-rg/p/5800859.html