BST、B树、B+树、B*树

标签：

一. BST

　　BST即二叉搜索树Binary Search Tree（又叫二叉排序树Binary Sort Tree）。它有以下特点：

1. 所有非叶子结点至多拥有两个儿子（Left和Right）；
2. 所有结点存储一个关键字；
3. 非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树。

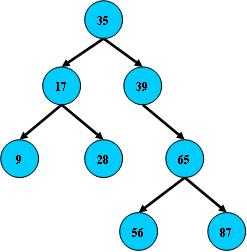
　　BST的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；如果B树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变B树结构（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销。

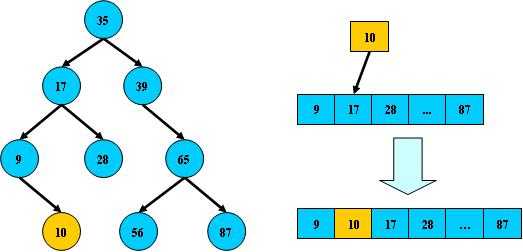
　　但BST树在经过多次插入与删除后，有可能导致不同的结构：

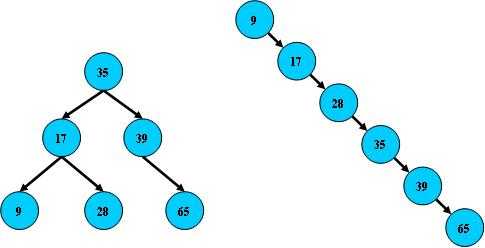
　　如上图所示，右边也是一个BST，但它的搜索性能已经是线性的了；同样的关键字集合有可能导致不同的树结构索引；所以，使用BST还要考虑尽可能让该树保持左图的结构，和避免右图的结构，也就是所谓的“平衡”问题；实际使用的BST都是在原BST的基础上加上平衡算法，即“平衡二叉树”；如何保持BST结点分布均匀的平衡算法是平衡二叉树的关键；平衡算法是一种在BST中插入和删除结点的策略。

二. B树（B-树）

　　B-tree树即B树，B即Balanced，平衡的意思。因为B树的原英文名称为B-tree，而国内很多人喜欢把B-tree译作B-树，其实，这是个非常不好的直译，很容易让人产生误解。而事实上是，B-tree就是指的B树。特此说明。

　　B-树是一种多路搜索树（并不一定是二叉的），它定义如下：

1. 定义任意非叶子结点最多只有M个儿子；且M>2；
2. 根结点的儿子数为[2, M]；
3. 除根结点以外的非叶子结点的儿子数为[M/2, M]；
4. 每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）
5. 非叶子结点的关键字个数=指向儿子的指针个数-1；
6. 非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
7. 非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
8. 所有叶子结点位于同一层；

　　当M=3时有如下示例：

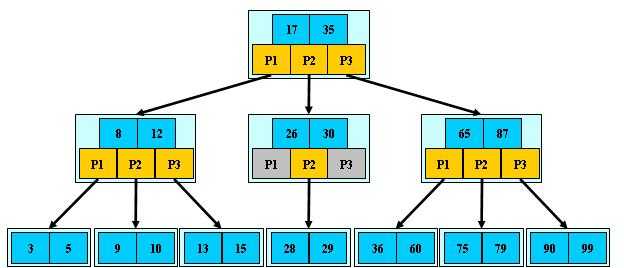
　　B树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点。

　　B树有以下特性：

1. 关键字集合分布在整颗树中；
2. 任何一个关键字出现且只出现在一个结点中；
3. 搜索有可能在非叶子结点结束；
4. 其搜索性能等价于在关键字全集内做一次二分查找；
5. 自动层次控制；

　　由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少利用率，其最底搜索性能为：

　　其中，M为设定的非叶子结点最多子树个数，N为关键字总数；所以B树的性能总是等价于二分查找（与M值无关），也就没有BST平衡的问题；由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并。

三. B+树

　　B+树是B-树的变体，也是一种多路搜索树。B+ 树是一个n叉树，每个节点通常有多个孩子，一棵B+树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点，也可能是一个包含两个或两个以上孩子节点的节点。B+树的定义如下：

1. 非叶子结点的子树指针与关键字个数相同；
2. 非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；
3. 为所有叶子结点增加一个链指针；
4. 所有关键字都在叶子结点出现；
5. 其他定义基本与B-树同。

　　当M=3时有如下示例：

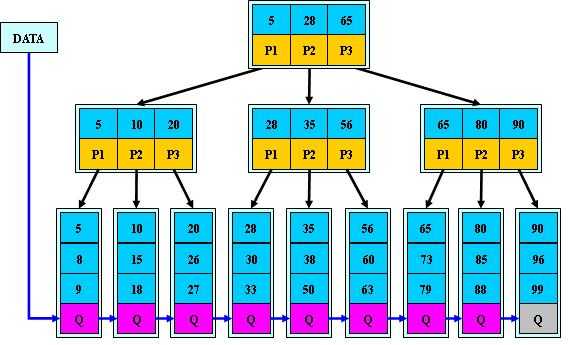
　　B+树有以下特性：

1. 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
2. 不可能在非叶子结点命中；
3. 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
4. 通常在B+树上有两个头指针，一个指向根结点，一个指向关键字最小的叶子结点。
5. 更适合文件索引系统。

　　一棵m阶的B+树和m阶的B-树的差异在于：

1. 有n棵子树的结点中含有n个关键字，每个关键字不保存数据，只用来索引，所有数据都保存在叶子节点。
2. 所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
3. 所有的非终端结点可以看成是索引部分，结点中仅含其子树（根结点）中的最大（或最小）关键字。

四. B*树

　　B*树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针。

　　当M=3时有如下示例：

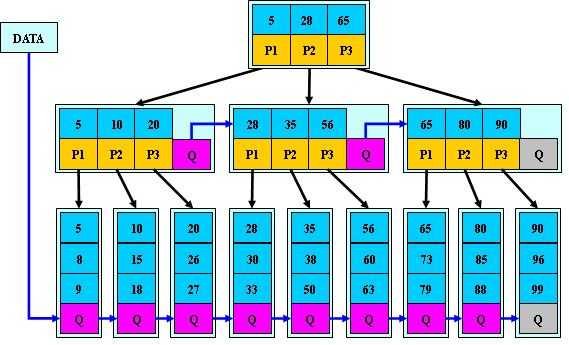
　　B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。

　　B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父

结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。

　　B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。

　　所以，B*树分配新结点的概率比B+树要低，空间使用率更高。

五. 小结

BST：每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点。

B(B-)树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中。

B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中。

B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3。

参考：http://www.cnblogs.com/oldhorse/archive/2009/11/16/1604009.html

BST、B树、B+树、B*树

标签：

原文地址：http://www.cnblogs.com/Eason-S/p/5809577.html