标签:
通常使用的分类回归树(class and regress tree)是一个二叉树。它的形式一般为: 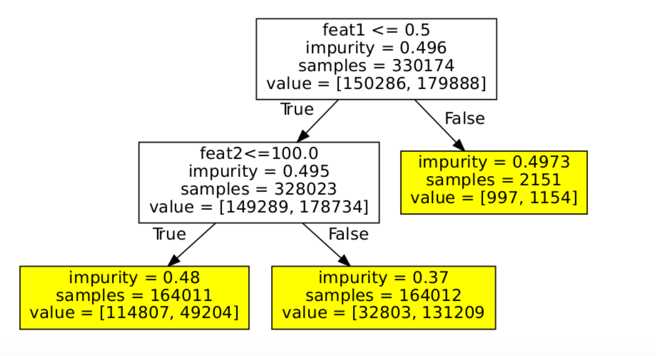
决策树有两种节点: 中间节点和叶子节点。
决策树最重要的概念就是不纯度函数(func I)的概念. 当一个节点需要分割的时候, 实际上就是找到一个合适的特征的一个合适的取值作为阈值(thresh)进行分割. 那么问题来了, 怎么找到那个合适的特征的合适的取值呢? 主要的依据就是不纯度的变化(delta I). 首先我们给出不纯度函数的定义. 不纯度函数不是一个具体的函数, 它是满足一系列约束的函数的总称.
在定义不纯度函数之前我们介绍一下机器学习的基本基本数学定义.
特征空间是一个 的矩阵, n表示样本个数(n_samples), m表示特征个数(n_features). 特征空间的第i个实例(instance)又叫做第i个特征向量, 使用
的矩阵, n表示样本个数(n_samples), m表示特征个数(n_features). 特征空间的第i个实例(instance)又叫做第i个特征向量, 使用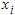 表示,:
表示,:
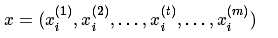
其中![]() 表示第i个实例的第t个特征.
表示第i个实例的第t个特征.
监督学习从训练数据(training data)集合中学习模型, 对测试数据(test data)进行预测. 训练数据由特征向量与输出对组成, 训练集合通常表示为:
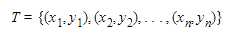
第i个输出yi表示输出向量第i个输出实例, 与第i个输入实例对应.
输出空间Y表示为为:
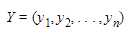
根据输出实例的取值范围不同. 决策树有不同的种类. 如果输出实例是离散的, 那么决策树是一个分类树; 如果输出实例是连续的, 那么决策树是一个回归树.如果决策树是分类树. 那么输出空间定义为输出实例所有取值的集合. 这个集合是有限集合. 不失一般性, 使用1,...,k这个取值. func I的定义为:
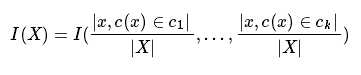
为了方便, 记:
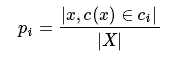
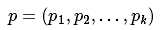
因此:
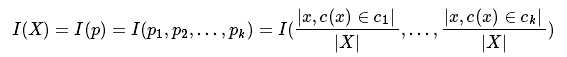
其中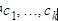 是对样本集合的一个划分:
是对样本集合的一个划分:
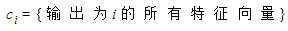
如上公式可以看出不纯度函数的定义域是长度为k的向量, 向量每个数的取值为0~1, 且加和为1. 第i个数是特征矩阵中属于类别i的特征向量个数在整个样本个数(n_sample)的占比.且必须满足如下约束:
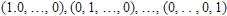 取最小值.
取最小值. 取最大值.
取最大值.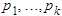 是对称的. 即
是对称的. 即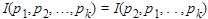 等. 从函数图像的角度理解, 就是函数一定是关于值坐标轴对称.
等. 从函数图像的角度理解, 就是函数一定是关于值坐标轴对称.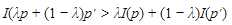
另外一个概念是不纯度变化(impurity reduction).
设 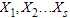 是特征空间X的一个划分. 不纯度变化定义为为:
是特征空间X的一个划分. 不纯度变化定义为为:
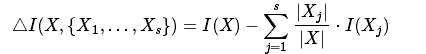
由于我们讨论的是二叉树, 我们简化一下公式:
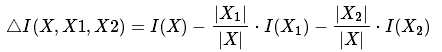
这个公式很好理解, X1,X2是对于原空间的一个划分. 按理说, 一个好的划分应该让不纯度变低, 以便让类目归属更加清晰. 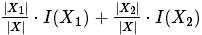 实际上就是这两个划分的不纯度的期望. 原不纯度减去划分后的不纯度的期望就是减少的不纯度的差值. 显然这个差值越大说明划分让子节点的纯度更"纯".
实际上就是这两个划分的不纯度的期望. 原不纯度减去划分后的不纯度的期望就是减少的不纯度的差值. 显然这个差值越大说明划分让子节点的纯度更"纯".
另外, 需要强调一点, 根据不纯度函数的第三个约束, 即不纯度函数是定义域下的凸函数, 可以保证 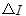 大于等于0.当且仅当所有划分的样本数相当取0.
大于等于0.当且仅当所有划分的样本数相当取0.
可这么说, 分类决策树节点划分的依据是找到一个特征的一个取值, 根据这个划分是的不纯度缩减量最大.
下面我们介绍两个常用不纯度函数, 信息熵(info entropy)和基尼指数(gini index).
首先介绍一下信息熵的概念. 我们把样本抽取过程当做一次随机试验A, 那么A有k个可能的输出 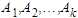 . 对应于k个分类. 那么A的信息熵定义为:
. 对应于k个分类. 那么A的信息熵定义为:
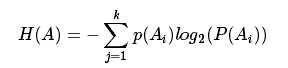
信息熵满足不纯度函数的定义. 所以我们定义:
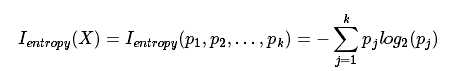
不纯度缩减(△I)为:
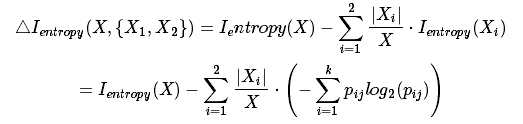
按照教课书的习惯, 当不纯度函数为信息熵是△Ientropy又叫做信息增益(info gain).
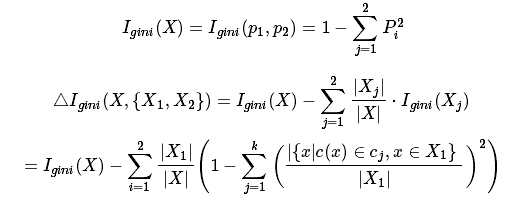
这里强调一下不管是信息熵还是基尼指数, 他们都是不纯函数的一种表达, 不纯度变化的计算没有任何变化. 我们也可以自己撰写不纯度函数. 当k=2时候, 我们可以吧信息熵和基尼指数在二维坐标上图形画出来. 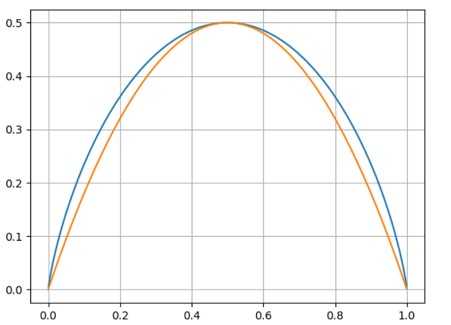
可以看出来这两个方法的区别很小. 实际过程中使用哪个方法作为不纯度函数效果不会有太大变化.
对于给定的训练集:
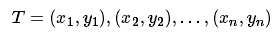
Y是连续变量. 考虑如何生成回归数.考虑一颗分类树, 每个叶子节点都对应一组概率值, 表示达到这个叶子节点的样本分到每个类目下的概率. 回归数基本结构和分类数一样, 不同的是每个叶子节点都表示对于到达这个叶子节点的样本的预测值(f(x)). f(x)等于这个叶子节点所有输入实例xi对应的输出yi的均值.有的叶子节点是对样本的一个划分
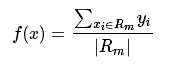
举个例子: 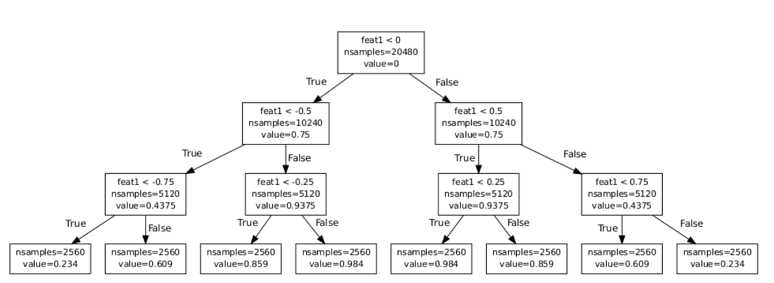
这颗回归树是对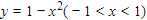 模拟, 我们把原函数和预测函数花在同一个坐标系统.
模拟, 我们把原函数和预测函数花在同一个坐标系统.
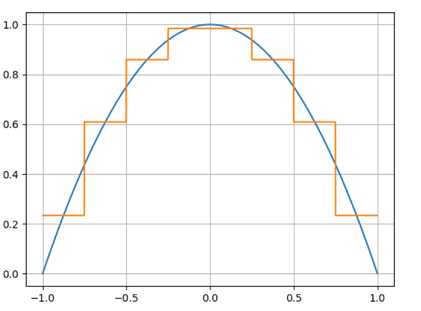
我看观察图形可以看出, 回归树的特点是使用连续的折线来拟合曲线. 因为在每个叶子节点的取值是固定的.
.回归树的构建和分类数构建方法类似. 同样是需要找个一个划分, 使得不纯函数的缩减最大. 但是上面所介绍的不纯度函数是根据分类树定义的. 我们需要定义适应回归树的不纯度函数.
在回归数中每个非叶子节点都是样本空间的一个子集的处理单元. 记这个子集为Tm每个样本xi有2个属性, 一个是实际输出yi, 另一个是预测输出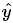 .
. 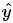 是通过这个节点下所有
是通过这个节点下所有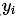 的均值算出来的, 即
的均值算出来的, 即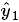 是
是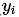 的期望. 反应的是总体上的拟合程度. 那么另外一个衡量
的期望. 反应的是总体上的拟合程度. 那么另外一个衡量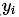 稳定性的指标是方差, 他衡量
稳定性的指标是方差, 他衡量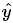 的代表性. 方差越小
的代表性. 方差越小
, 说明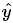 越具有代表性. 因此我们可以定义一种不纯度函数, 就是这个节点下输出值的方差.
越具有代表性. 因此我们可以定义一种不纯度函数, 就是这个节点下输出值的方差.
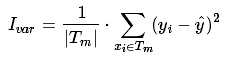
那么:
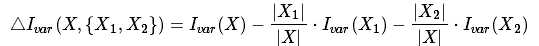
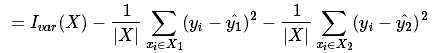
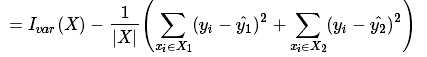
值得注意的是, 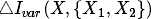 和
和 对于当前节点来说是常数. 因此
对于当前节点来说是常数. 因此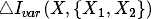 和
和 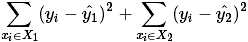 是单调性是相反的. 最大化前者就是最小化后者. 一般的教科书直接写成这样的公式:
是单调性是相反的. 最大化前者就是最小化后者. 一般的教科书直接写成这样的公式:
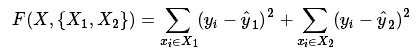
目标是找到合适的特征的值使得△I最大或者F最小. 这个不纯函数一般叫做最小二乘函数(MSE).
上面介绍了决策树一个重要概念, 不纯函数. 不纯函数不仅是分类树的概念, 也是回归树的概念. 它们在形式上是统一的. 这点很有意义, 下面我们分析sklearn源码时候可以发现, 在设计>决策树时候没有区分分类和回归树, 他们的不同都被封装在不纯函数的定义和计算节点的输出中了.
上面一章介绍了分类和回归数在某个节点如何选择合适的特征和特征取值进行分裂. 这一章介绍决策树的构建方法, 即如何决定每步应该分裂的节点. 决策树的构建一般有2种方法:
| 名称 | 图像 | 说明 |
|---|---|---|
| 广度优先 | 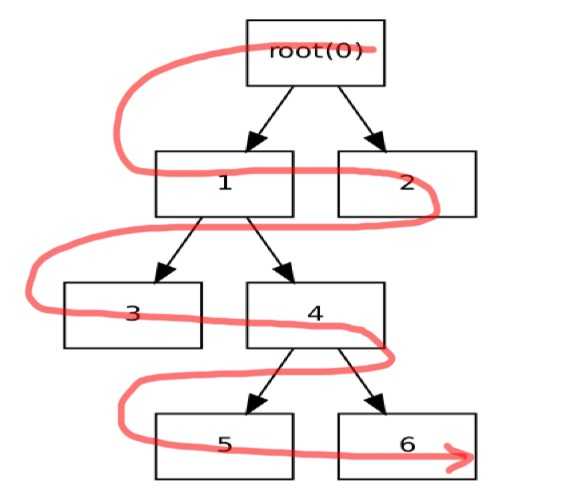 |
广度优先按照层次来构建树的. 首先根据合适的不纯度函数来分裂root成2个节点; 然后依次分裂第二层的2个节点; 依次递推. |
| 深度优先 | 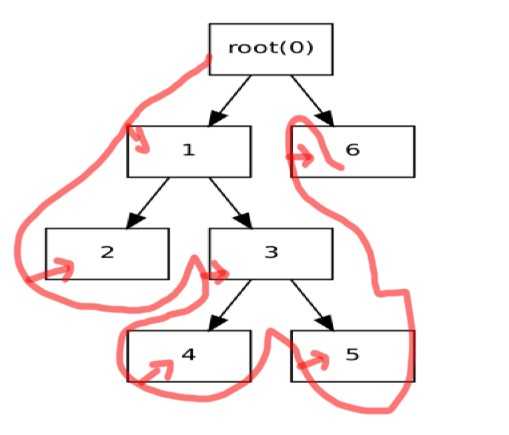 |
深度优先采用递归的思想, 在每个节点都是优先有左边的子树建好, 再建右边子树 |
不管是深度优先还是广度优先, 决策树算法都需要知道什么时候一个节点应该作为叶子节点. 如果没有约束决策树会一直建设下去知道节点只有一个类目(或者只有一个取值)才停止. 这样会>导致决策树变得非常庞大, 引发过拟合问题.
一般来说, 当如下条件其中之一满足的时候, 当前节点停止构建, 作为决策树的叶子节点.
| 参数 | 意义 | 终止条件 |
|---|---|---|
| min_samples_split | 当前节点允许分裂的最小样本数 | 当前节点样本数小于这个值时候 |
| min_samples_leaf | 叶子节点最少样本数 | 任何分裂不能导致子节点的样本数小于此值, 否则禁止分裂 |
| min_impurity_split | 分裂的不纯度阈值 | 当前节点不纯度小于此值时不分裂 |
| max_path | 数的最大深度 | 当前节点的深度大于等于此值是不分裂 |
通过上述的说明, 决策树的预测就非常的简单了. 决策树中只有叶子节点有预测功能. 一个测试样本从root出发选择正确的路径, 一定会走到一个叶子节点. 叶子节点的值即为决策树对这个>样本的预测.
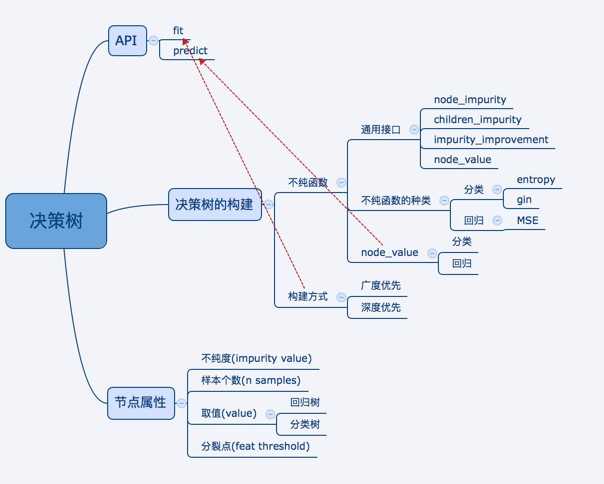
本文的结构实际上就是按照sckit-learn中的决策树进行设计的. 源代码在: https://github.com/scikit-learn/scikit-learn/tree/master/sklearn/tree .
首先介绍一下主要文件:
criterion.py* 主要定义了各种不纯度函数及其计算和转化方法.
| 主要类 | 功能描述 |
|---|---|
| abstract Criterion | 定义一系列计算某个不纯度或者不纯度缩减的方法 1. node_impurity: 计算当前节点的不纯度 2. children_impurity: 计算2个子节点的不纯度 3. impurity_improvement: 计算当前节点的不纯度缩减量 4. proxy_impurity_improvement: 由于当前节点的不纯度是一个常数, 因此在比较不纯度缩减量时候有更加简单的方法, 这个方法是回归数是, 计算所有样本输出的均值, 作为输出值. 5. node_value: 当前节点的值, 用于预测. 当决策树是分类树时它计算每个类目的概率, 当决策树 在分裂过程中最常用, impurity_improvement仅当需要计算不纯度缩减绝对值时才用 |
| Class ClassificationCriterion | 继承 Criterion; 重写node_value方法, 适应分类树的计算| |
| Class Entropy | 各个方法, 符合entropy的定义impurity继承ClassificationCriterion; |
| Class Gini | 继承ClassificationCriterion; |
| Class RegressionCriterion | 继承 Criterion; 重写node_value方法, 适应回归树的计算 |
| class MSE | 继承 RegressionCriterion , 主要实现上文提到回归数的不纯度计算方法 |
这个文件是讲所有的功能拼装在一起形成一个可以独立使用决策树类. 首先它声明了一个TreeBuilder的系列类, 用于实现前文所说的深度优先建树和广度优先建树.
这是源代码中为唯一一个python文件(其他都是cython文件). 他主要封装了_tree.py* 定义和主流机器学习库兼容的方法体系.
本章, 我们给出一个完整的实例.
import numpy as npfrom sklearn.tree importDecisionTreeRegressorimport matplotlib.pyplot as plt# Create a random datasetrng = np.random.RandomState(1)X = np.sort(5* rng.rand(80,1), axis=0)y = np.sin(X).ravel()y[::5]+=3*(0.5- rng.rand(16))# Fit regression modelregr_1 =DecisionTreeRegressor(max_depth=2)regr_2 =DecisionTreeRegressor(max_depth=5)regr_1.fit(X, y)regr_2.fit(X, y)# PredictX_test = np.arange(0.0,5.0,0.01)[:, np.newaxis]y_1 = regr_1.predict(X_test)y_2 = regr_2.predict(X_test)# Plot the resultsplt.figure()plt.scatter(X, y, c="k", label="data")plt.plot(X_test, y_1, c="g", label="max_depth=2", linewidth=2)plt.plot(X_test, y_2, c="r", label="max_depth=5", linewidth=2)plt.xlabel("data")plt.ylabel("target")plt.title("Decision Tree Regression")plt.legend()plt.show()这个实例很简单. 首先需要使用DecisionTreeRegressor来声明一个回归树. 然后使用fit来训练, 最后使用predict来预测结果.
这个实例展示了max_depth的不同, 对于效果的影响. 可以看到max_depth=5时候已经有过拟合现象了(有很多抖动点).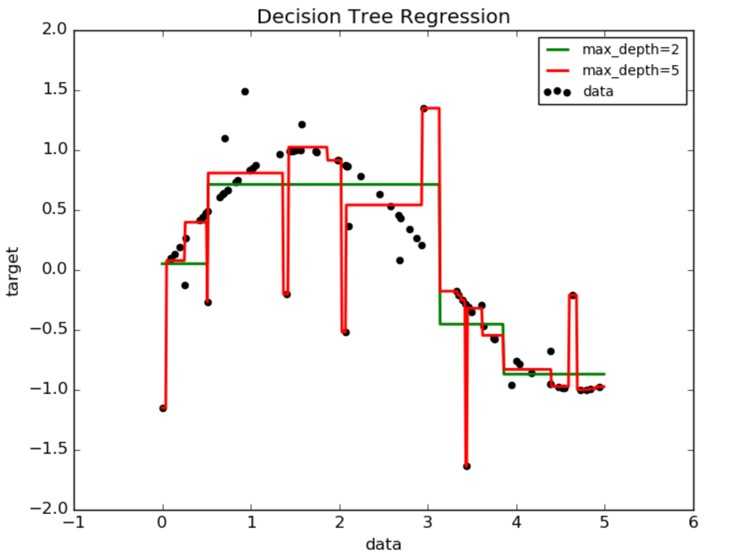
我们进一步改进, 维持max_depth=5不变, 增加min_samples_leaf=5的参数. 效果进一步提升. 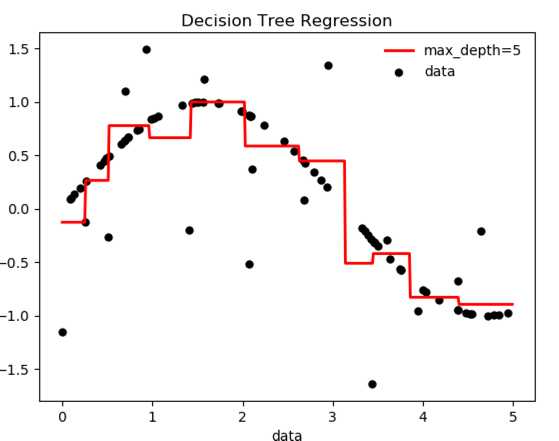
可以看到参数对于决策树的质量来说非常重要.
一般来说, 机器学习都需要特征归一化, 目的是让特征之间的比较可以在同一个量纲上进行. 但是从数据构建过程来看, 不纯函数的计算和比较都是单特征的. 所有决策树不需要数据的归一>化. 但是有点需要注意, 从上文中对splitter的源码分析中可以看出, 决策树为了加速遍历没有真正遍历所有取值, 当特征的绝对值太小的时候会导致相邻值的间隔小于step, 因此尽量让特>征值不要太小(大于0.01比较保险).
在gini函数小节中我们比较了gini和entroy在两元下的图形. 可以看到基本上没有区别. 有研究表明不同的不纯度函数对决策树产生的影响在2%以内1.
有人做过一项实验, 说明gini和entroy的不同:
gini更倾向于孤立最大的分类, 而entroy更加倾向于把类目均等分割. 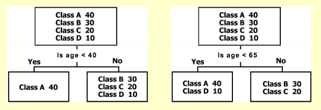
但是这也只是一种微弱的倾向, 事实上很少有实际案例说明选择不纯度函数有显著的作用. 所以对于分类决策树选择gini, 对于回归选择MSE, 这样的默认配置可以满足绝大多数的需求.
决策树的重要参数都是防止过拟合的. 我认为2个参数一定要设置:
我们回到 公式的本身:
公式的本身:
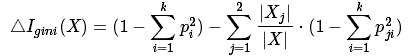
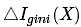 取到最大值. 很明显这是一个算法上的偏见, 已经形成了过拟合
取到最大值. 很明显这是一个算法上的偏见, 已经形成了过拟合
决策树的主要问题是容易形成过拟合. 如果我们通过各种剪枝和条件限制, 虽然可以避免过拟合, 但是会牺牲特征的有效性. 举个例子:
在构造决策树的过程中我们可以断言节点个数不会超过100个, 这样很多feature不仅没有多次分裂, 甚至有些特征根本无法参与决策.
为了解决这个问题, 统计学家不再深入决策树的结构而是提出另外一个思路: 能够通过构造不同的简单的决策树共同决策? 这有点"三个臭皮匠顶一个诸葛亮"的感觉. 我会在下一个文章具体>介绍一下这个方法, 即随机森林. 它是一个非常有效和常用的机器学习算法.
标签:
原文地址:http://www.cnblogs.com/hsydj/p/5814263.html