标签:
这一章节将介绍一系列典型的微积分问题(求极限、级数、定积分、导数、重积分等)在Matlab中的求解。
首先关于极限:
(1) 数列极限:
给出下面三段例程。

求解数列极限的limit函数参数说明:可以看到该函数可以有三个参数也可以有两个参数,对于三个变量(比如说第二个例程),第一个参数是数列的通项,第二个参数是确认离散变量,因为在通项中有两个字母a、n,第三个参数表示这个离散变量趋于某个范围,这个函数将返回在离散变量趋于的那个范围(第三个参数)时的极限。
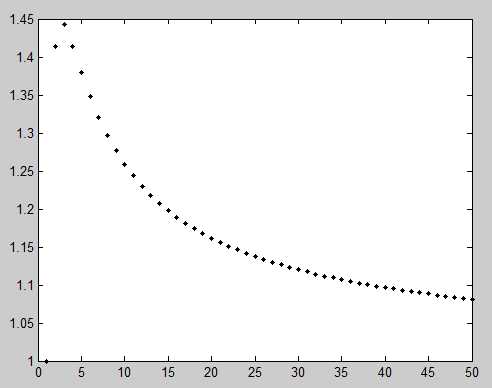
当然,借助Matlab自身强大的图像功能,我们对于求解数列极限,我们还有一个可行的方法就是得到这个数列的散点图,通过观察这个数列趋近于一个怎样的数,但是散点的数量要始终,而且得到的结果很可能不准确。
那第一个例子来说:
>> n=1:50;
>> plot(n,n.^(1./n),‘k.‘) % k.这里表示制自变量整数位置的散点图
得到如下的大致图像:
导数和微分在Matlab中的求解:
对于最简单的一阶导数,基于之前我们介绍的极限在Matlab中的写法,可根据定义直接求出导函数。
定义法求导函数:
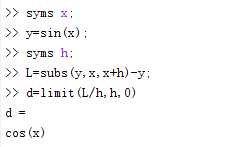
diff函数直接求导函数:
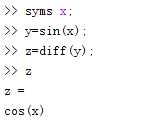
基于定义法和左右导数的概念所编写的DerivativeDefinition函数:
function df=DerivativeDefinition(fun,x,x0,type) %DERIVATIVEDEFINITION 根据导数的定义求函数的导函数或在某点处导数值 % DF=DERIVATIVEDEFINITION(FUN,X)或 % DF=DERIVATIVEDEFINITION(FUN,X,[]) 求函数FUN关于X的导函数 % DF=DERIVATIVEDEFINITION(FUN,X,X0) 求函数FUN在点X0处的导函数 % DF=DERIVATIVEDEFINITION(FUN,X,X0,TYPE) 根据TYPE指定导数类型求函数在点X0处的导数, % TYPE有以下取值: % 1.‘double‘或0:双侧导数值,此为缺省值 % 2.‘left‘或-1:左导数 % 3.‘right‘或1:右导数 % DF=DERIVATIVEDEFINITION(FUN,X,[],TYPE) 根据TYPE指定导数类型求函数的导函数 % % 输入参数: % ---FUN:符号函数表达式 % ---X:符号自变量 % ---X0:求导点 % ---TYPE:导数类型 % 输出参数: % ---DF:返回的导函数或导数值 % % See also limit, diff if nargin<4 type=0; end if nargin==2 || isempty(x0) x0=x; end syms h delta_y=subs(fun,x,x0+h)-subs(fun,x,x0); switch type case {0,‘double‘} df=limit(delta_y/h,h,0); % 求导数 case {-1,‘left‘} df=limit(delta_y/h,h,0,‘left‘); % 求左导数 case {1,‘right‘} df=limit(delta_y/h,h,0,‘right‘); % 求右导数 otherwise error(‘The Style of Derivative is Illegal.‘) end
结合一个实际问题对这段代码进行应用。
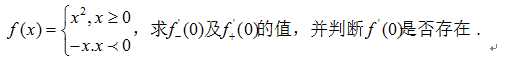

根据结果可知该点导数并不存在。
这里值得提的一点是,为了实现Matlab自定义函数功能,需要在Matlab编辑器中定义函数及其功能,然后在命令行窗口进行编程计算时直接调用即可。
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5814391.html