标签:
关于SVM(support vector machine)--支持向量机的一个故事
很久很久以前,有个SVM, 然后,……………………被deep learning 杀死了……………………………………
完结……撒花
故事的起源:
好吧,关于支持向量机有一个故事 ,故事是这样子的:
在很久以前的情人节,大侠要去救他的爱人,但魔鬼和他玩了一个游戏。
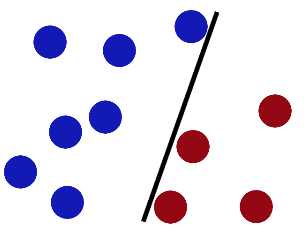
魔鬼在桌子上似乎有规律放了两种颜色的球,说:“你用一根棍分开它们?要求:尽量在放更多球之后,仍然适用。”
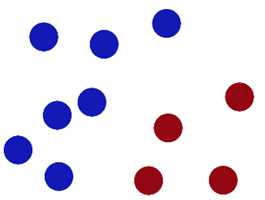
于是大侠这样放,干的不错?
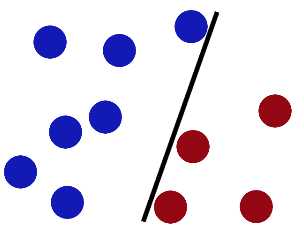
然后魔鬼,又在桌上放了更多的球,似乎有一个球站错了阵营。
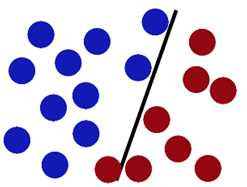
SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能大的间隙
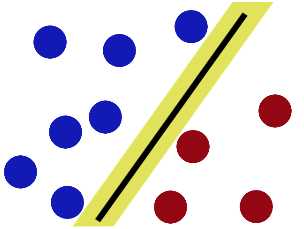
现在即使魔鬼放了更多的球,棍仍然是一个好的分界线
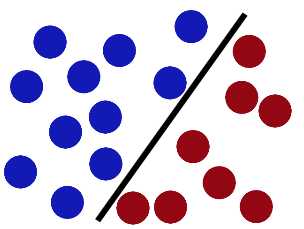
然后,在SVM 工具箱中有另一个更加重要的 trick。 魔鬼看到大侠已经学会了一个trick,于是魔鬼给了大侠一个新的挑战。
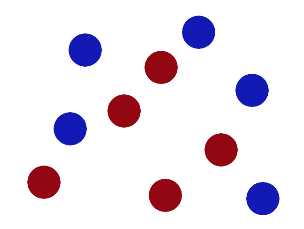
现在,大侠没有棍可以很好帮他分开两种球了,现在怎么办呢?当然像所有武侠片中一样大侠桌子一拍,球飞到空中。然后,凭借大侠的轻功,大侠抓起一张纸,插到了两种球的中间。
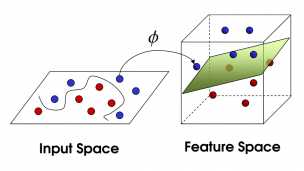
现在,从魔鬼的角度看这些球,这些球看起来像是被一条曲线分开了。
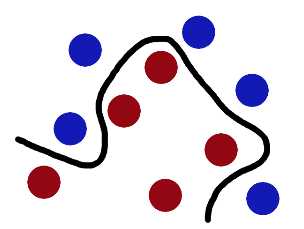
再之后,无聊的大人们,把这些球叫做 「data」,把棍子 叫做 「classifier」, 最大间隙trick 叫做「optimization」, 拍桌子叫做「kernelling」, 那张纸叫做「hyperplane」。
正文开始:
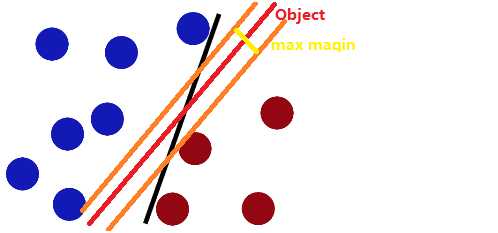
svmSVM的意义究竟是怎样的?首先是一堆需要分类的数据,就一维数据而言,目标是找到其使其可分离的分界点,二维数据而言就是,使其分离的线,就三维而言,就是使其分离的平面。这个分界线与两类数据最近的点则称为max-margin(最大边缘)。当然,简单的说下图中黑线位置可以是我们找到分界线.然而这个并非是最优的.通常而言,我们渴望所得到最大边缘是越大越好的,这样表示这个找到的最大Margin,是最优的,即下图黄线.也就是说,这样的分界线能够很好的将两类数据进行分离,即下图红线。而我们选择数据在进行训练的时候也就是为了能够找到很好的分界线,这样,当测试数据进来,依据在红色线位置,我们可以进行分类。ok,现在的问题是给了我这样的一大堆数据,我事先也是知道的,这些数据是怎样区分的,SVM是一种监督式学习方法的原因也在于此。
问题出现了,我们要如何找到这个分界线。假定我们是有这样的数据的,(x1, y1), (x2, y2), ...,(xn, yn), x用来代表数据,它可以是任意维度的,而y是表示代表的数据究竟是一个正样本,还是负样本,(即这个样本是属于A,还是属于B).
这就是回到了之前的问题,如何找到这样的一条线:
,首先我们假设,这个给出我们对数据的判定规则,给定一条直线的公式为:
y=WTX+b,
如果使得y > 0,则为正样本,y < 0则为负样本,我们的目标就很明确的知道,这样我们的目标就变成了找到y=0,这个直线.也就是为了能够求出W,b这两个参数.
有没有很奇怪,为什么这里的W会有一个转置符号?
其实,不可以单纯的理解为W是一个值,这里是一个向量(我已经加粗了,思密达)这里是为了考虑多维的情况.
就二维而言,而上面的橙色线我们有一个名字,support hyperplane(支撑平面).这两个直线的公式为:
WTX =δ+b
WTX =δ-b,
由于这里的W,b是未知参数,这个公式随意的在两边乘以一个非零参数,仍然不变,所以我们可以令δ=1.,这样我们就得到max margin 的距离公式,即:
,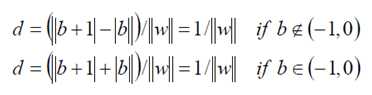
其中两倍的d即为 margin.所margin = 2d = 2/||W||,而为了获得最大的 (max) margin,其实就是想找最小的||W||。我们的约束条件是,对于任意的正样本:
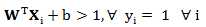
对于任意的负样本:
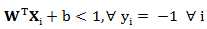
这个限制条件是我们进行接下来处理的关键,同时这连个式子可以合并为:
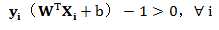
于是我们得到以下目标公式:
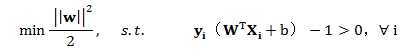
而这个问题就是SVM的核心,通过这个问题就可以求解出W,b,上式中的最小化问题其实就是我们要进行分类的数学表达形式。其中除以2,只是为了后续的结果好看,并不影响最终结果。其中这里面的取平方有着比较重要的意义,这里后面将会提到。(ps:这里的取平方和不去平方的意义是相同的--之前是为了获得最大的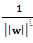 ,现在是为了获得最小的
,现在是为了获得最小的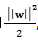
,问题是等价的)
前面所说的是线性可分的情况,这时,如果是线性不可分,即如下图所示:
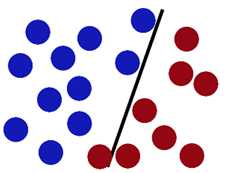
这种情况下,如果我们只是单纯的考虑让其可分,这是不可能的。因为他们本来就分不开。这样我们就引入了一个误差选项,ε,我们是允许在分类过程中出现误差的,用以保证其在整体的最优。(即,不能因为一个老鼠而坏了一锅汤)。所以我们的判决条件变为:
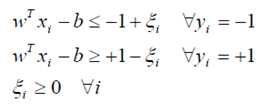
当然,这个误差项是我们自行调节的,如果太大,我们得到的分界线(面or something else, max margin),就会容错性太强(错的太多),大到一定程度,这样我们还要这个分界线干么?
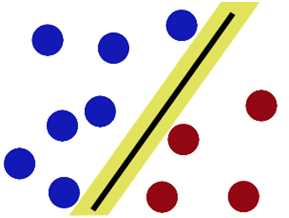
所以我们是希望有点误差,但是希望这个误差不要太大。这样我们的正负样本又能快乐的分类了。不会因为个别的样本影响到整体的分类结果。于是我们又引入了一个惩罚因子C,这样总体可忍受误差变为:
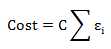
这样我们刚才的目标函数就变为:
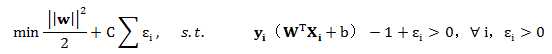
这两种目标函数代表svm的两种形式(hard-margin and soft-margin)。这个问题和上面的一样目标一样是一个QP问题(Quadratic programming),其实问题只要不是NP问题,数学家总有办法求解。至此线性分类结束。
然而实际中,可能存在的是无法分类的情况,这样的:
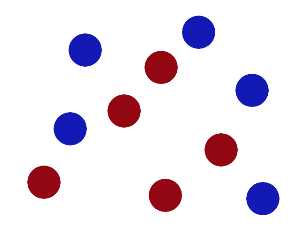
所以,这个问题怎么求解?如果还想找到那样的一个分界线,很明显,是不可能的。
于是我们便引入了一个SVM实际用途很重要的一种形式:kernel--核函数
这样先回到最初的目标函数:
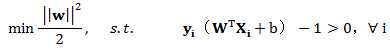
引入拉格朗日乘子,上式的问题可以变为:
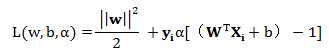
即目标问题变为求 的最小值问题,我们知道,一般这样的极值点通常是在其导数等于零时取得,于是对w,b 分别求偏微分,可以得到:
,
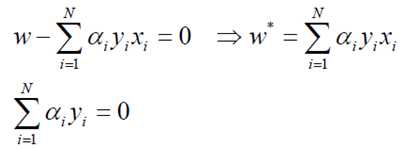
将得到的结果带入初始目标函数,这样激动人心的时刻到了,原目标函数变为:
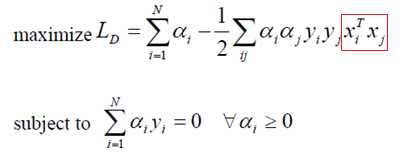
目标函数变为上面这样,这里需要指出的是,这里的
y都是常量,只有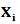 为一个多维向量。如果原始数据
是不可分,如上所示,那么我们可以让
为一个多维向量。如果原始数据
是不可分,如上所示,那么我们可以让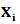 以
以 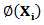
进行线性映射到其他空间,这样上面红色框内就变成:
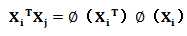
这样在原来空间计算的问题就转换为映射空间的问题,也就是
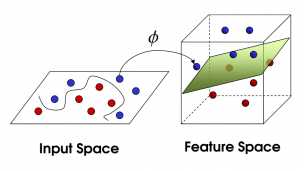
是不是,很吃惊,当我看到这,我也很吃惊。上述的转换是有深层含义的,如果我们的数据维度很低,只是在二维空间的一个点的位置,那么我们有多种方式进行分类,KNN等也许都可以,毕竟计算量并不大。关键是如果我们的维度很高,甚至接近无限维,这样我们再进行分类,有些分类方案不太适合,而这种方案由于计算的内积,计算的结果是一个值,这样即使很高维度的依然可以转换向量内积来计算,大大的减少了计算量。(个人理解)。于是原来的问题就可以分类了,就是这样。
除了上述的线性映射,还有其他种类的:
多项式核(Polynomial Kernel)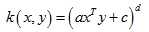
径向基核函数(RBF)(Radial Basis Function)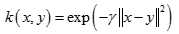
也叫高斯核(Gaussian Kernel),因为可以看成如下核函数的领一个种形式: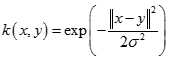
径向基函数是指取值仅仅依赖于特定点距离的实值函数,也就是 。任意一个满足 特性的函数 Φ都叫做径向量函数,标准的一般使用欧氏距离,尽管其他距离函数也是可以的。
。
至此关于SVM的基础就是这样,具体的证明可以参考下面的文档。
最后,我的愿望是……
世界和平,阿门
参考文档:
1:http://www.dataguru.cn/forum.php?mod=viewthread&tid=371987
--核函数相关,那个会转的图不错
2:http://blog.csdn.net/v_july_v/article/details/7624837
--SVM大全,从入门到放弃
3:http://www.csie.ntu.edu.tw/~cjlin/libsvm/
--一个很不错的svm网站,内部有个黑框,可以自行调整参数C,ε,对线性核RBF核会有个直观感受
4:http://blog.csdn.net/abcjennifer/article/details/7849812
--SVM的细致推导,源自一个网易公开课,
5:https://en.wikipedia.org/wiki/Support_vector_machine
--wiki百科--自由的百科全书
6:http://open.163.com/movie/2008/1/C/6/M6SGF6VB4_M6SGJVMC6.html
---Andrew Ng,机器学习大神
标签:
原文地址:http://www.cnblogs.com/sunbinbin/p/5827449.html