标签:
Given n non-negative integers representing the histogram‘s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given heights = [2,1,5,6,2,3],
return 10.
【题目分析】
题目很容易理解,给定一个非负数组代表的直方图,求出图中包含的最大的矩形的面积。
【思路】
1.这题的一个基本思想是以每一个bar为最低点,向左右遍历直到遇到比他小的bar或边界。这样就能找到一个此bar为最低点的矩形面积。遍历所有的bar之后即可找到最大的矩形面积。但是向左右遍历寻找比他小的bar的时间复杂度是O(n),在加上遍历一遍所有的bar,总的时间复杂度将为O(n*n),是无法通过所有数据的。我们在水平方向任意画一条线,如果有条和这条线相交,我们找出相交的矩阵中最大的那个。示例如下:
当线的高度是2时,相交的矩阵有两个,较大的那个面积是8。
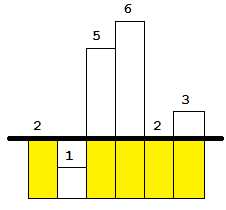
当线的高度是3时,相交的矩阵有两个,较大的那个面积时6。
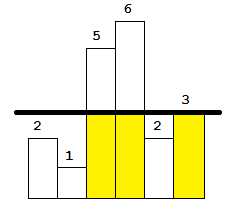
当线的高度是5时,相交的矩阵有一个,面积是10。
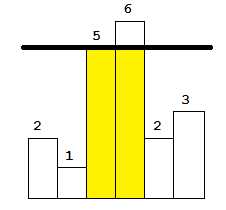
重复上面的步骤,找到的最大值是10.这个过程很简单,只需要遍历所有可能出现的高度,然后找到所有出现的矩阵中面积最大的那一个。但是这个过程的算法复杂度较高,为O(N2).
java代码:
1 public class Solution { 2 public int largestRectangleArea(int[] heights) { 3 if(heights.length == 0) return 0; 4 if(heights.length == 1) return heights[0]; 5 6 int curlen = 0; 7 int maxS = 0, curS = 0; 8 9 for(int i = 0; i < heights.length; i++){ 10 curlen = heights[i]; 11 curS = 0; 12 for(int j = 0; j < heights.length; j++){ 13 if(heights[j] >= preminlen) curS += preminlen; 14 else{ 15 maxS = Math.max(curS, maxS); 16 curS = 0; 17 } 18 } 19 maxS = Math.max(curS, maxS); 20 } 21 return maxS; 22 } 23 }
2. 我们需要寻找一种时间复杂度更低的寻找一个bar左右边界的算法。在网上流传了一个设计极其巧妙的方法,借助一个stack可以将时间复杂度降为O(n)。
这种算法的思想是维护一个递增的栈,这个栈保存了元素在数组中的位置。 这样在栈中每一个左边的bar都比本身小,所以左边就天然有界了,也就是左边界就是左边的一个bar。遍历一遍height数组,在将height数组入栈的时候,如果当前元素height[i]比栈顶元素小,则我们又找到了栈顶元素的右边界。因此我们在此时就可以计算以栈顶元素为最低bar的矩形面积了,因为左右边界我们都已经找到了,而且是在O(1)的时间复杂度内找到的。然后就可以将栈顶元素出栈了。这样每出栈一个元素,即计算以此元素为最低点的矩形面积。当最终栈空的时候我们就计算出了以所有bar为最低点的矩形面积。为保证让所有元素都出栈,我们在height数组最后加一个0,因为一个元素要出栈必须要遇到一个比他小的元素,也就是右边界。
java代码:
1 public class Solution { 2 public int largestRectangleArea(int[] height) { 3 int len = height.length; 4 Stack<Integer> s = new Stack<Integer>(); 5 int maxArea = 0; 6 for(int i = 0; i <= len; i++){ 7 int h = (i == len ? 0 : height[i]); 8 if(s.isEmpty() || h >= height[s.peek()]){ 9 s.push(i); 10 }else{ 11 int tp = s.pop(); 12 maxArea = Math.max(maxArea, height[tp] * (s.isEmpty() ? i : i - 1 - s.peek())); 13 i--; 14 } 15 } 16 return maxArea; 17 } 18 }
LeetCode OJ 84. Largest Rectangle in Histogram
标签:
原文地址:http://www.cnblogs.com/liujinhong/p/5837841.html