标签:
二叉堆堆是一个数组,它可以被看成一个近似的完全二叉树,树上每一个结点对应数组中的一个元素。除了最底层外,该树是完全充满的,而且是从左到右填充。表示堆的数组A包括两个属性:A.length给出数组元素的个数,A.heap_size表示有多少个堆元素存储在该数组中,这里,0<=A.heap_size<=A.length。
如下图所示:
堆可以分成两种:最大堆和最小堆。在最大堆中,任何节点的值都大于等于其孩子的值,故根节点是数组中的最大数所在节点。反之,最小堆中,任何节点的值都小于等于其孩子的值,故根节点是数组中最小值所在节点。
最小堆如下:
优先队列是一种用来维护由一组元素构成的集合S的数据结构,其中的每一个元素都有一个相关的值,称为关键字。优先队列也分为两种:最大优先队列和最小优先队列。
一个最大优先队列支持以下操作:
•INSERT(S,x):把元素x插入集合S中;
•MAXIMUM(S):返回S中具有最大关键字的元素;
•EXTRACT_MAX(S):去掉并且返回S中的具有最大关键字的元素;
•INCREASE_KEY(S,x,k):将元素x的关键字值增加到k。
相应地,最小优先队列支持的操作包括INSERT、MINIMUM、EXTRAT_MIN和DECRESE_KEY。
由于二叉堆就是一个简单的一维Int数组,故不需要初始化,直接插入便可。
每次插入都将新数据放到数组的最后的位置,最小堆原理如图:
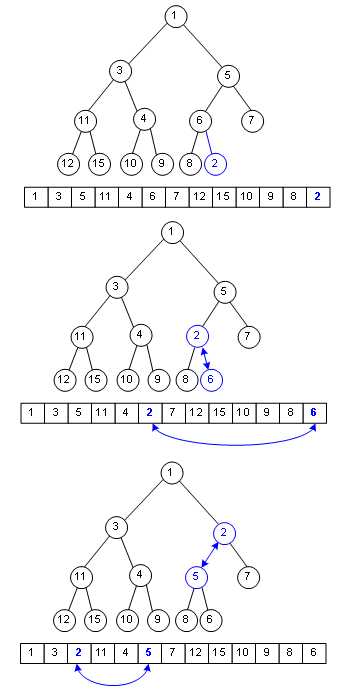
假设要在这个二叉堆里入队一个单元,键值为2,那只需在数组末尾加入这个元素,然后尽可能把这个元素往上挪,直到挪不动,经过了这种复杂度为Ο(logn)的操作,二叉堆还是二叉堆。
核心代码如下:

1 //A为该数组,i是新数据所在下标 2 void Insert(int A[], int i,int heap_size) 3 { 4 int j, temp; 5 6 temp = A[i]; 7 j = i / 2; //父结点 8 while (j >= 1 && i != 1) 9 { 10 if (A[j] <= temp) 11 break; 12 13 A[i] = A[j]; //把较大的子结点往下移动,替换它的子结点 14 i = j; 15 j = i / 2; 16 } 17 A[i] = temp; 18 heap_size ++; 19 }
按定义,堆中每次都只能删除第1个数据。为了便于重建堆,实际的操作是将最后一个数据的值赋给根结点,然后再从根结点开始进行一次从上向下的调整。调整时先在左右儿子结点中找最小的,如果父结点比这个最小的子结点还小说明不需要调整了,反之将父结点和它交换后再考虑后面的结点。相当于从根结点将一个数据的“下沉”过程。
下面给出代码:

1 //先进行调整 2 void MinHeapify(int A[],int i,int heap_size) 3 { 4 int l = 2*i; 5 int r = 2*i+1; 6 int minimum; 7 if(l <= heap_size && A[l] < A[i]) 8 minimum = l; 9 else 10 minimum = i; 11 if(r <= heap_size && A[r] > A[minimum]) 12 minimum = r; 13 if(largest != i) 14 { 15 swap(A[i],A[minimum]); 16 MinHeapify(minimum,heapsize); 17 } 18 } 19 20 //然后删除 21 void Delete(int A[],int heap_size) 22 { 23 Swap(A[1],A[heap_size]); 24 heap_size --; 25 MinHeapify(A,1,heap_size); 26 }
有了堆的插入和删除后,再考虑下如何对一个数据进行堆化操作。
核心代码如下:

1 //N是数组中元素个数 2 void BuildMinHeap(int A[],int N,int heap_size) 3 { 4 int heap_size = N; 5 for(int i = N/2;i > 0;i--) 6 MinHeapify(A,i,heap_size); 7 }
核心算法如下:

1 void HeapSort(int A[],int heap_size,int N) 2 { 3 int heap_size = N; 4 BuildMinHeap(A,N,heap_size); 5 for(int i = N;i > 1;i--) 6 { 7 Swap(A[1],A[i]); 8 heap_size --; 9 MinHeapify(A,1,heap_size); 10 } 11 }
在用堆实现优先的过程中,需要注意最大堆只能对应最大优先队列,最小堆则是对应最小优先队列,核心代码如下:

1 void INCREASE_KEY(int A[],int i,int key) 2 { 3 if (key < A[i]) 4 cout <= "error!"; 5 A[i] = key; 6 while (i > 1 && A[i/2] < A[i]) 7 { 8 swap(A[i],A[i/2]); 9 i = i/2; 10 } 11 } 12 13 void INSERT(int A[],int key,int heap_size) 14 { 15 heap_size ++; 16 A[heap_size] = MIN; //MAX为负无穷 17 INCREASE_KEY(A,heap_size,key); 18 } 19 20 int MAXIMUM(int A[]) 21 { 22 return A[1]; 23 } 24 25 int EXTRACT_MAX(int A[],int heap_size) 26 { 27 if (heap_size < 1) 28 cout <= "error!"; 29 int max = A[1]; 30 A[1] = A[heap_size]; 31 heap_size --; 32 MAX_HEAPIFY(A,1,heap_size); //应该很好根据前面的分析写出来 33 }
以上代码的写法有些欠妥,用struct和全局变量写应该会方便很多,各位多多体谅!
标签:
原文地址:http://www.cnblogs.com/vachester/p/5840217.html