标签：des   style   http   color   java   os   io   strong   

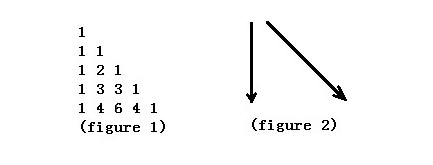
尽量沿着边走距离最短，化减后 C（n+1，k）+ n - k，

预处理阶乘，Lucas定理组合数取模

DP?

Figure 1 shows the Yang Hui Triangle. We number the row from top to bottom 0,1,2,…and the column from left to right 0,1,2,….If using C(n,k) represents the number of row n, column k. The Yang Hui Triangle has a regular pattern as follows.
C(n,0)=C(n,n)=1 (n ≥ 0) 
C(n,k)=C(n-1,k-1)+C(n-1,k) (0<k<n)
Write a program that calculates the minimum sum of numbers passed on a route that starts at the top and ends at row n, column k. Each step can go either straight down or diagonally down to the right like figure 2.
As the answer may be very large, you only need to output the answer mod p which is a prime.

1 1 2
4 2 7

Case #1: 0
Case #2: 5

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long int LL;

LL n,k,p;

LL fact[1300][11000];

LL QuickPow(LL x,LL t,LL m)
{
	if(t==0) return 1LL;
	LL e=x,ret=1LL;
	while(t)
	{
		if(t&1LL) ret=(ret*e)%m;
		e=(e*e)%m;
		t>>=1LL;
	}
	return ret%m;
}

int prime[2000],pr;
bool vis[10100];

void get_prime()
{
	for(int i=2;i<10100;i++)
	{
		if(vis[i]==false)	
			prime[pr++]=i;
		for(int j=2*i;j<10100;j+=i)
			vis[j]=true;
	}
}

void get_fact()
{
	for(int i=0;i<1240;i++)
	{
		fact[i][0]=1LL;
		for(int j=1;j<=prime[i]+10;j++)	
		{
			fact[i][j]=(fact[i][j-1]*j)%prime[i];	
		}
	}
}

LL Lucas(LL n,LL m,LL p)
{
	LL ret=1LL;
	int id=lower_bound(prime,prime+pr,p)-prime;
	while(n&&m)
	{
		LL a=n%p,b=m%p;
		if(a<b) return 0;
		ret=(ret*fact[id][a]*QuickPow((fact[id][b]*fact[id][a-b])%p,p-2,p)%p)%p;
		n/=p; m/=p;
	}
	return ret%p;
}

int main()
{
	get_prime();
	get_fact();
	int cas=1;
	while(scanf("%I64d%I64d%I64d",&n,&k,&p)!=EOF)
	{
		if(k>n/2) k=n-k;
		LL ans=(Lucas(n+1,k,p)+n-k)%p;
		printf("Case #%d: %I64d\n",cas++,ans);
	}
	return 0;
}

HDOJ 4349 DP?,布布扣,bubuko.com

HDOJ 4349 DP?

标签：des   style   http   color   java   os   io   strong   

原文地址：http://blog.csdn.net/ck_boss/article/details/38479839