标签:
今天用将近一天的时间学习了层次分析模型(AHP),主要参考了一份pdf,这个网站,和暨南大学章老师的课件,现写出一些自己总结的要点。
一、层次分析法的基本步骤:
角度一:
实际问题——分解——>多个因素——建立——>层次结构—
—确定——>诸因素的相对重要性——计算——>权向量—
—判断——>综合决策
角度二:
建立层次结构模型——>构造判断矩阵——>层次单排序——>一致性检验——>层次总排序。
二、几个理解的重点
1.正反矩阵
注意:

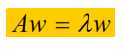
这里想了下,用最大特征根的特征向量替代A,可能是为了最大限度的保存原始数据(A)的信息量(不确定。。。)
3.一致性检验

一致性检验,具体还要涉及组合一致性检验。
三、MATLAB实现
这里先是搜的资料,看到这段代码,代码写得很清晰,这里直接贴在这里。
clc;
clear;
A=[1 1.2 1.5 1.5;
0.833 1 1.2 1.2;
0.667 0.833 1 1.2;
0.667 0.833 0.833 1];
%因素对比矩阵A,只需要改变矩阵A
[m,n]=size(A); %获取指标个数
RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];
R=rank(A); %求判断矩阵的秩
[V,D]=eig(A); %求判断矩阵的特征值和特征向量,V特征值,D特征向量;
tz=max(D);
B=max(tz); %最大特征值
[row, col]=find(D==B); %最大特征值所在位置
C=V(:,col); %对应特征向量
CI=(B-n)/(n-1); %计算一致性检验指标CI
CR=CI/RI(1,n);
if CR<0.10
disp(‘CI=‘);disp(CI);
disp(‘CR=‘);disp(CR);
disp(‘对比矩阵A通过一致性检验,各向量权重向量Q为:‘);
Q=zeros(n,1);
for i=1:n
Q(i,1)=C(i,1)/sum(C(:,1)); %特征向量标准化
end
Q %输出权重向量
else
disp(‘对比矩阵A未通过一致性检验,需对对比矩阵A重新构造‘);
end
这里是对AHP的一个初步的认识,之后还要深入学习,到时候再继续总结。
标签:
原文地址:http://www.cnblogs.com/buzhizhitong/p/5844139.html