标签:
高等代数
一、行列式
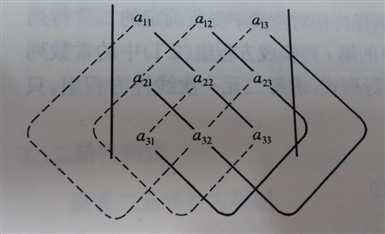
1.1求三阶行列式:
计算方法:按图计算,实线为正号,虚线为负号
1.2求n阶行列式
1)计算排列逆序数
例1:求32154的逆序数:
答:0+1+2+0+1=4
例2:求n(n-1)...21的逆序数:
答:n(n-1)/2
2)计算公式:逆序数为奇数取负,为偶数取正。
注意是按行顺序取数:a1p1,a2p2,...,anpn
1.3行列式D的性质
1、D=DT
2、互换行列式2行(列),D改变正负号。
3、D中存在2行(列)完全相同,则D为0
4、D中存在元素全为0的某行(列),则D为0
5、D中存在两行(列)对应元素成比例,则D为0
6、行列式某一行(列)中所有元素同乘以k,等于k*D,即可以将公因子提到行列式外面
7、D的对某一行加上k*另一行,则D不变
证明:
1.4元素aij的代数余子式Aij
1、公式
Aij=(-1)i+j*Mij
其中Mij是D的余子式,它由行列式D去掉元素aij去掉第i行j列后剩下的(n-1)个元素保持原位置组成的n-1阶行列式。
2、求行列式:行列式的展开法则
D=ai1Ai1+ai2Ai2+...+ainAin(i=1,2,...,n)
例:
二、矩阵
2.1运算律
加法:
1)交换律:A+B=B+A
2)结合律:(A+B)+C=A+(B+C)
数乘:
1)结合律:(λμ)A=λ(μA)
2)分配率:λ(A+B)=λA+λB,(λ+μ)A=λA+μA
2.2矩阵乘法
2.2.1公式
2.2.2运算律
1)结合律:(AB)C=A(BC)
2)分配律:A(B+C)=AB+AC,(B+C)A=BA+CA
3)λ(AB)=(λA)B=A(λB)
4)AE=A
5)A的幂运算:AkAl=Ak+l,(Ak)l=Akl
2.3转置矩阵AT的运算律
1)(AT)T=A
2)(A+B)T=AT+BT
3)(λA)T=λAT,λ为数
4)(AB)T=BTAT推广到(A1A2...Al)T=AlTAl-1T...AlT
2.4方阵
2.4.1行列式det(A)的运算律
1)|AT|=|A|
2)|λA|=λn|A|
3)|AB|=|AB|
2.4.2逆矩阵
1)公式
设A为n阶方阵,若存在一个n阶方阵B使
AB=BA=E
则称A是可逆的,B为A的逆矩阵。
2)A的伴随矩阵A*
其中,A*中的元素Aij是|A|中aij的代数余子式。
3)性质
1)AA*=A*A=|A|E
2)(A-1)-1=A
3)(λA)-1=1/λ A-1(λ!=0)
4)|A-1|=|A|-1
5)(AT)-1=(A-1)T
6)A可逆,B可逆,AB也可逆,且(AB)-1=B-1A-1
- 奇异矩阵:A为方阵,|A|=0;
- 非奇异矩阵:A为方阵,|A|!=0;
若矩阵A可逆,则|A|!=0
2.5矩阵的秩与初等变换
2.5.1秩
矩阵A的r阶子式D不等于0,而A的所有r+1阶子式全为0,则r称为矩阵A的秩,记为R(A)=r。其中零矩阵的秩为0。
2.5.2初等变换
2.5.2.1定义
1)对调某两行ri<-->rj
2)以数k!=0乘以某一行中所有元素kri
3)把某一行所有元素的k倍加到另一行对应元素上ri+krj
等价矩阵:矩阵A初等变换得到的矩阵B。记为A~B
2.5.2.2性质
1)对A施行一次初等行变换相当于在Am*n的左边乘以初等矩阵Pm*m;对A施行一次初等列变换相当于在A的右边乘以初等矩阵Qn*n
2)可逆矩阵A可标识成有限个初等矩阵的乘积A=P1P2...Pl,由此可得
P-1(A|E)=(E|A-1)
A-1(A|B)=(E|A-1B)
例1:求A-1
答:利用公式P-1(A|E)=(E|A-1)
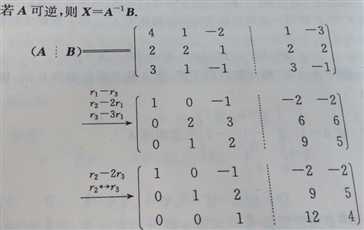
例2:求A-1B
答:利用公式A-1(A|B)=(E|A-1B)
三、方阵的特征值与特征向量
3.1定义
1)特征值与特征向量
设A是一个n阶方阵,λ是一个数,如果方程
或
存在非零解向量X,则称λ为A的一个特征值,对应的X为特征值相应的特征向量。
2)特征方程
这是n个未知数x,n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式
即
上式是以λ为未知数的一元次方程,称为方阵A的特征方程:
因为特征方程的解就是A的特征值λ。特征方程在复数范围内恒有解,其个数为方程的次数(重根按重数计算),因此,n阶矩阵A有n个特征值。
3.2求解特征值和特征向量
例:
3.3性质
1)属于不同特征值的特征向量一定线性无关。
2)λ
3)相似:就是之前的等价矩阵
则称A与B相似,记作A~B ,且满秩矩阵P称为将A变为B的相似变换矩阵。
- 相似矩阵有相同的特征多项式,因而有相同的特征值。
- 若阶矩阵与对角矩阵
相似,则
 即是A的n个特征值。
即是A的n个特征值。
4)特征值与矩阵的阶数没有任何关系,可以取任意大的值。只有在主成分分析和因子分析里才强调最大特征值λ。
参考资料:
1、李宏伟,李星,李志明,《工程高等代数》,科学出版社
【数理统计】高等代数
标签:
原文地址:http://www.cnblogs.com/xuancaoyy/p/5845321.html
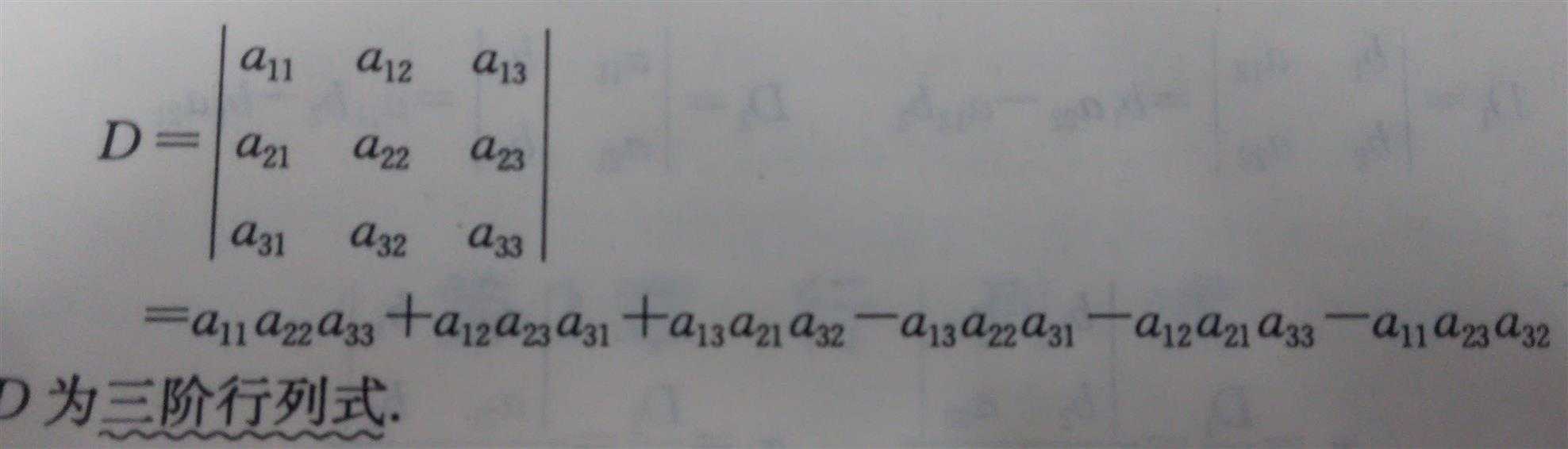


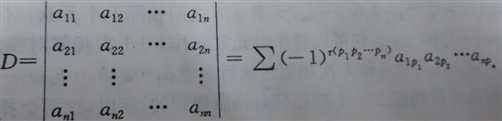





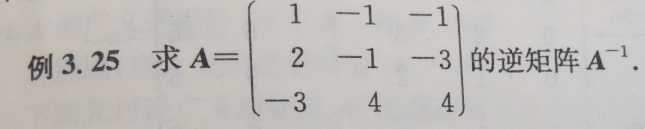
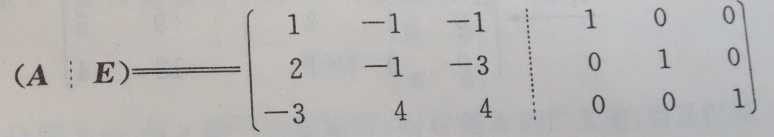

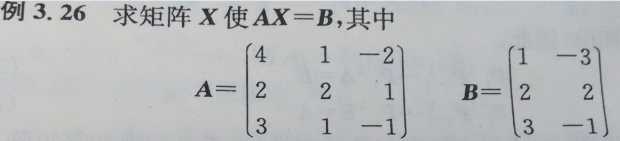



 =
=


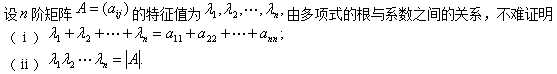


 即是A的n个特征值。
即是A的n个特征值。