标签:
树的定义有两种:
1.是基于图论的定义;
2.是基于递归和节点的定义;
1.基于图论的定义:
如果一个无向简单图G 满足以下相互等价的条件之一,那么G 是一棵树:
 不是G的子图。
不是G的子图。如果无向简单图G有有限个顶点(设为n个顶点),那么G 是一棵树还等价于:
如果一个无向简单图G中没有简单回路,那么G是森林。
2.基于节点和递归的定义:
树(Tree)是n(n≥0)个有限数据元素的集合。当n=0 时,称这棵树为空树。在一棵非树T 中:
(1)有一个特殊的数据元素称为树的根结点,根结点没有前驱结点。
(2)若n>1,除根结点之外的其余数据元素被分成m(m>0)个互不相交的集合T1,T2,…,Tm,其中每一个集合Ti(1≤i≤m)本身又是一棵树。树T1,T2,…,Tm 称为这个根结点的子树。
可以看出,在树的定义中用了递归概念,即用树来定义树。因此,树结构的算法类同于二叉树结构的算法,也可以使用递归方法。
树的定义还可形式化的描述为二元组的形式:
其中D 为树T 中结点的集合,R 为树中结点之间关系的集合。
当树为空树时,D=Φ;当树T 不为空树时有:
其中,Root 为树T 的根结点,DF 为树T 的根Root 的子树集合。DF 可由下式表示:
当树T 中结点个数n≤1 时,R=Φ;当树T 中结点个数n>1 时有:
其中,Root 为树T 的根结点,ri 是树T 的根结点Root 的子树Ti 的根结点。
树定义的形式化,主要用于树的理论描述。图7.1(a)是一棵具有9 个结点的树,即T={A,B,C,…,H,I},结点A 为树T 的根结点,除根结点A 之外的其余结点分为两个不相交的集合: T1={B,D,E,F,H,I}和T2={C,G},T1 和T2 构成了结点A 的两棵子树,T1 和T2 本身也分别是一棵树。例如,子树T1 的根结点为B,其余结点又分为两个不相交的集合:T11={D},T12={E,H,I}和T13={F}。
T11、T12 和T13 构成了子树T1 的根结点B 的三棵子树。如此可继续向下分为更小的子树,直到每棵子树只有一个根结点为止。
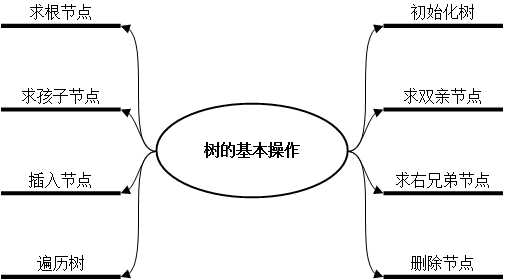
从树的定义和图7.1(a)的示例可以看出,树具有下面两个特点:
(1)树的根结点没有前驱结点,除根结点之外的所有结点有且只有一个前驱结点。
(2)树中所有结点可以有零个或多个后继结点。
由此特点可知,图7.1(b)、(c)、(d)所示的都不是树结构。

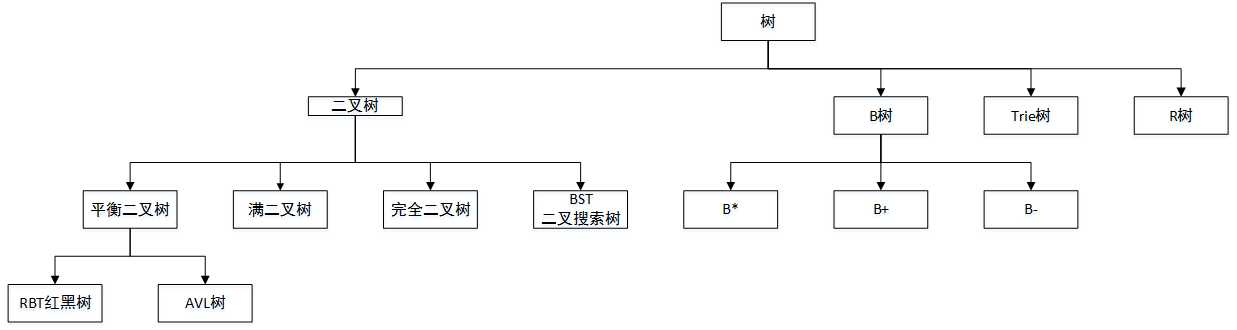
| 二叉树 |
|
|---|
| 自平衡二叉查找树 |
|
|---|
| B树 |
|
|---|
| Trie |
|
|---|
| 空间划分树 |
|
|---|
| 非二叉树 |
|
|---|
| 其他类型 |
|
|---|
|
树的名称 |
应用场景 |
|
Trie树 |
特点:保证字典序,存储字典的空间压缩率高 |
|
前缀搜索 |
|
|
正则匹配 |
|
|
数据压缩 |
|
|
数据库构建索引 |
|
|
|
C++ |
|
四叉树、八叉树 |
机器人领域,检测碰撞 |
|
|
文件系统的目录结构 |
|
|
路由协议 |
|
哈夫曼树 |
编码、压缩 |
|
B树、B+ |
分布式系统、mysql |
|
BST二叉查找树 |
内存查找 |
|
AVL自平衡二叉树 |
内存查找 |
参考链接:
http://c.biancheng.net/cpp/html/985.html
https://zh.wikipedia.org/wiki/%E6%A0%91_(%E5%9B%BE%E8%AE%BA)
http://philoscience.iteye.com/blog/1112759
标签:
原文地址:http://www.cnblogs.com/x739400043/p/5846673.html