标签:
在计算机科学中随机数永远会被用到。我的初衷是对随机数在蒙特卡洛模拟中的频繁使用状况进行管理。域的数据空间相当大,足够详尽地测试所有可能性,这样我就可以考察模拟中随机对输入参数赋值并产生海量输出结果的情况,这些输出结果可以用许多静态方法验证。比如,你可以按上面的方法利用随机数计算PI的值。(注:蒙特卡洛方法是使用随机数来解决很多计算问题的方法)
[假使你不知道是否能用上述方法完成计算,你有必要花几分钟思考一下。网络上有许多有趣的方法。其中甚至包括掷飞镖!下面的链接能帮你在自己的浏览器中利用随机数进行计算,链接还附上了JS样例。样例链接:https://curiosity-driven.org/pi-approximation]
一旦你理解了(或者尝试阅读其他的简单方法),这方法在你看来便是优雅且合理的。但是它还有潜在的缺陷,就是它极度依赖被用于产生蒙特卡罗测试要素的数字的真正随机性。算法预测随机数的生成拥有均匀的概率分布。如果你正在生成0.0~1.0之间的随机浮点数,任何一个数字出现的概率必须和其他数字相同。假如0.5附近的数出现的概率稍稍高于其他数,那么你最终得到的结果便会存在偏差,会偏向错误答案。在我提到的JS样例中很容易发现,更多的点落在圆内,由于点的数目表示它所在的圆区域,圆区域与正方形的比值也会偏大。因此电脑计算出的PI值也会偏大。
[在思考分布的均匀性时还需要考虑一个问题:你的取样量有多大?样例分布均匀是前半部分与后半部分都均匀吗?如果你运行一个JS脚本,你可能会觉得观察PI的估值不断变化是有趣的事。也许JS随机数生成器还不够完美?]
随机数不仅要绝对无序,而且它们要保证等概率出现以使任何的蒙特卡洛模拟都能正常运行。
无论你使用的是哪种计算机语言,所附的大多数随机数生成器并不是真正随机。它们是具有确定性的算法。我们使用的随机函数通常指的是伪随机数生成器。它们被设计成适当地生成均匀分布的无规律数字。
但这样就够了吗?我会在下一篇进行说明。
参考:经过12小时的蒙特卡罗仿真,PI的估值为3.14154XXXXXX.
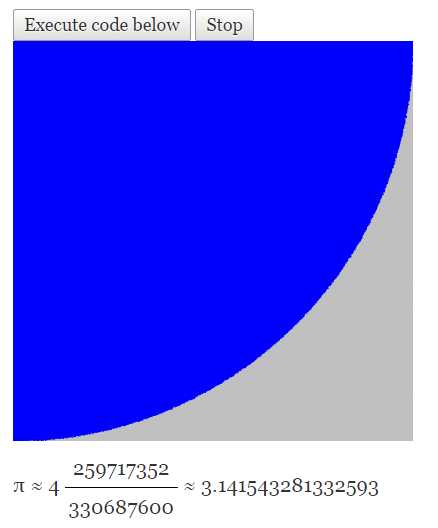
这个偏离是可以接受的吗?假如再增加12小时,答案会更优吗?这些是大家需要思考的随机性问题。
注:本文为译文。
原文链接:https://dzone.com/articles/the-randomness-of-being
随机的本质(一)
标签:
原文地址:http://www.cnblogs.com/panshijie205/p/5847196.html
