标签:
欧拉函数这里理论性非常强,它与费马小定理、剩余系、素数分解定理联系,能够推导出一系列的定理。
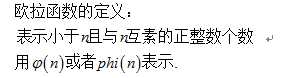



计算phi(n)的编码实现:
#include<cstdlib> #include<iostream> using namespace std; int phi(int n) { int rea = n; for(int i = 2;i*i <=n;i++) if(n%i == 0) { rea = rea - rea/i; do n /= i; while(n%i == 0); } if(n > 1) rea = rea - rea/n; return rea; } int main() { int n; while(cin >> n && n) { cout << phi(n) << endl; } return 0; }
计算区间[1,n]上欧拉函数值的和phi(2)+phi(3)+…+phi(n):
当n取得较大整数时,如果用上文求单个整数的欧拉函数值然后相加,耗时太多,这里对于求区间欧拉函数值的和,有一个类似Eratosthenes筛法的优化。
那么这里我们就像筛选素数那样,得到一个素数然后设置第二层循环记录这个素数整数倍的整数的“不完整欧拉值”,当该整数所有的素因子都遍历到,欧拉值便更新到真实值。
#include <cstdio> //O(nloglogn) #include <cstdlib> #include <cstring> #include <cmath> using namespace std; const int SIZE = 1000000 + 5; int phi[SIZE]; void init() { int i, j; memset(phi, 0, sizeof(phi)); phi[1] = 1; for(int i = 2; i < SIZE; i++) if(!phi[i]) { for(j = i; j < SIZE; j+=i) { if(!phi[j]) phi[j] = j; phi[j] = phi[j] / i * (i-1); } } } int main() { init(); int n; while(scanf("%d",&n)!=EOF && n) { long long sum = 0; for(int i = 2; i <= n; i++) { sum += phi[i]; } printf("%lld\n",sum); } }
应用1:既约真分数(poj 2478).
给出整数n,让你求解分母小于n的所有既约真分数的个数。
分析:首先我们要搞懂什么是既约真分数,简单来说,就是小于1的最简分数。那么我们很容易将其与欧拉函数联系起来,因为对于一个分母为n的既约真分数的个数,实际上就是phi(n),那么这个问题本质上就是求解phi(2)+...+phi(n).
应用2:精简打表数据.(uva 10820)
有一道比赛题目,输入两个整数x、y(均小于等于n),输出某个函数值f(x,y),一位选手想打表,但是如果全部打出来的话会造成内存超限,需要精简。
这道题目可以通过f(x,y)计算出f(kx,ky),k是任意正整数,这样很多结果就不需要放在表中了。
分析:通过“f(x,y)计算f(x,y)”这个题设条件,我们就能够将其联想到欧拉函数。最终表中存的二元组(x,y)只要互素,就能够保证表中不存在任何“赘余(即可由表中的另外某组数据计算得来)”数据.
假设x>y,那么我们枚举x=2、3、…、n,二元组的数量应该是phi(2)+…+phi(n),由对称性,最终结果应该乘2,而且不要忘记了(1,1)这个特殊情况。
最终结果应该是2(phi(2)+…+phi(n)) + 1.
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5848329.html