标签:
CNN是一种多层神经网络,基于人工神经网络,在人工神经网络前,用滤波器进行特征抽取,使用卷积核作为特征抽取器,自动训练特征抽取器,就是说卷积核以及阈值参数这些都需要由网络去学习。
图像可以直接作为网络的输入,避免了传统识别算法中复杂的特征提取和数据重建过程。
一般卷积神经网络的结构:
前面feature extraction部分体现了CNN的特点,feature extraction部分最后的输出可以作为分类器的输入。这个分类器你可以用softmax或RBF等等。
权值共享减少了权值数量,降低了网络复杂度。
其中,tanh(·)是双曲正切函数,bij为属于特征图Oij的可训练偏置,Kij为与Oij相连的第i-1层中特征图标号的集合。Wijk是连接特征图Oij和特征图O(i-1)k的卷积核窗口,Ri和Ci分别为该层卷积核的行数和列数。若第i-l层特征图的大小为n1×n2,连接第i-1层特征图和第i层特征图的卷积核大小为I1×12,则第i层特征图的大小为(n1-l1+1)×(n2-l2+1).
mean-pooling、max-pooling。
down(Xjl-1)表示下采样操作,就是对一个小区域进行pooling操作,使数据降维。
有的算法还会对mean-pooling、max-pooling后的输出进行非线性映射
f是激活函数。
Evaluation of Pooling Operations in. Convolutional Architectures for Object Recognition这篇文献证明了最大池一般效果更好。
貌似现在已经有用histogram做pooling的了。
注意,卷积的计算窗口是有重叠的,而采用的计算窗口没有重叠。
一般来说深度神经网络中的激活函数选用RELU而不用sigmoid或tanh。
ReLU(x)=max(x,0)
原因如下:
链接:http://www.zhihu.com/question/29021768/answer/43488153
来源:知乎
第一,采用sigmoid等函数,反向传播求误差梯度时,求导计算量很大,而Relu求导非常容易。(这个不大认同,sigmoid求导可以直接给出公式:f‘(x) = f(x)[1-f(x)])
第二,对于深层网络,sigmoid函数反向传播时,很容易就会出现梯度消失的情况(在sigmoid接近饱和区时,变换太缓慢,导数趋于0),从而无法完成深层网络的训练。
第三,Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
sigmoid和tanh函数的图像如下:
很自然的看到他们的导数两端接近0.
1. 传统的激励函数,计算时要用指数或者三角函数,计算量至少要比简单的 ReLU 高两个数量级;
2. ReLU 的导数是常数,非零即一,不存在传统激励函数在反向传播计算中的"梯度消失问题";
3. 由于统计上,约一半的神经元在计算过程中输出为零,使用 ReLU 的模型计算效率更高,而且自然而然的形成了所谓 "稀疏表征" (sparse representation),用少量的神经元可以高效,灵活,稳健地表达抽象复杂的概念。最后一个卷积-采样层的输出可作为输出层的输入,输出层是全连接层。输出层是一个权值可微的分类器,可以让整个网络使用基于梯度的学习方法来进行全局训练,比如softmax、RBF网络、 一层或两层的全连接神经网络等分类算法。但即使不可微的分类器(比如svm)其实也可以使用的,方法是先用可微的分类器调参数,参数调好后把分类器换掉就行了。
以LeNet5为例,其结构如下:
C1,C3,C5 : Convolutional layer.
5 × 5 Convolution matrix.
S2 , S4 : Subsampling layer.
Subsampling by factor 2.
F6 : Fully connected layer
OUTPUT : RBF
C层和S层成对出现,C承担特征抽取,S承担抗变形。C元中涉及两个重要参数,即感受野与阈值参数,前者确定输入连接的数目,后者则控制对特征子模式的反应程度。
C1层是一个卷积层(通过卷积运算,可以增强图像的某种特征,并且降低噪音),由6个特征图Feature Map构成。Feature Map中每个神经元与输入中5*5的邻域相连。特征图的大小为28*28。C1有156个可训练参数(每个滤波器5*5=25个unit参数和一个bias参数,一共6个滤波器,共(5*5+1)*6=156个参数),共156*(28*28)=122,304个连接。
S2层是一个下采样层,有6个14*14的特征图。特征图中的每个单元与C1中相对应特征图的2*2邻域相连接。S2层每个单元的4个输入相加,乘以一个可训练参数,再加上一个可训练偏置。结果通过sigmoid函数计算。可训练系数和偏置控制着sigmoid函数的非线性程度。如果系数比较小,那么运算近似于线性运算,亚采样相当于模糊图像。如果系数比较大,根据偏置的大小亚采样可以被看成是有噪声的“或”运算或者有噪声的“与”运算。每个单元的2*2感受野并不重叠,因此S2中每个特征图的大小是C1中特征图大小的1/4(行和列各1/2)。S2层有12个可训练参数和5880个连接。
C3层也是一个卷积层,它同样通过5x5的卷积核去卷积层S2,然后得到的特征map就只有10x10个神经元,但是它有16种不同的卷积核,所以就存在16个特征map了。这里需要注意的一点是:C3中的每个特征map是连接到S2中的所有6个或者几个特征map的,表示本层的特征map是上一层提取到的特征map的不同组合。
S4层是一个下采样层,由16个5*5大小的特征图构成。特征图中的每个单元与C3中相应特征图的2*2邻域相连接,跟C1和S2之间的连接一样。S4层有32个可训练参数(每个特征图1个因子和一个偏置)和2000个连接。
C5层是一个卷积层,有120个特征图。每个单元与S4层的全部16个单元的5*5邻域相连。由于S4层特征图的大小也为5*5(同滤波器一样),故C5特征图的大小为1*1:这构成了S4和C5之间的全连接。之所以仍将C5标示为卷积层而非全相联层,是因为如果LeNet-5的输入变大,而其他的保持不变,那么此时特征图的维数就会比1*1大。C5层有48120个可训练连接。
F6层有84个单元(之所以选这个数字的原因来自于输出层的设计),与C5层全相连。有10164个可训练参数。如同经典神经网络,F6层计算输入向量和权重向量之间的点积,再加上一个偏置。然后将其传递给sigmoid函数产生单元i的一个状态。
最后,输出层由欧式径向基函数(Euclidean Radial Basis Function)单元组成,每类一个单元,每个有84个输入。换句话说,每个输出RBF单元计算输入向量和参数向量之间的欧式距离。输入离参数向量越远,RBF输出的越大。一个RBF输出可以被理解为衡量输入模式和与RBF相关联类的一个模型的匹配程度的惩罚项。用概率术语来说,RBF输出可以被理解为F6层配置空间的高斯分布的负log-likelihood。给定一个输入模式,损失函数应能使得F6的配置与RBF参数向量(即模式的期望分类)足够接近。这些单元的参数是人工选取并保持固定的(至少初始时候如此)。这些参数向量的成分被设为-1或1。虽然这些参数可以以-1和1等概率的方式任选,或者构成一个纠错码,但是被设计成一个相应字符类的7*12大小(即84)的格式化图片。
分类器中的全连接层需要以卷积的形式来实现,即以卷积核和输入大小一样的卷积操作来实现全连接。
卷积核和偏置在开始时要随机初始化,这些参数是要在训练过程中学习的。卷积核[-sqrt(6 / (fan_in + fan_out)), sqrt(6 / (fan_in + fan_out))] 的取值范围选择来自于Bengio 的Understanding the difficulty of training deep feedforward neuralnetworks这篇文章。
卷积核的另一种初始化方法是用autoencoder去学习参数。
反向传输过程是CNN最复杂的地方,虽然从宏观上来看基本思想跟BP一样,都是通过最小化残差来调整权重和偏置,但CNN的网络结构并不像BP那样单一,对不同的结构处理方式不一样,而且因为权重共享,使得计算残差变得很困难,很多论文[1][5]和文章[4]都进行了详细的讲述,但我发现还是有一些细节没有讲明白,特别是采样层的残差计算,我会在这里详细讲述。
4.1输出层的残差
和BP一样,CNN的输出层的残差与中间层的残差计算方式不同,输出层的残差是输出值与类标值得误差值,而中间各层的残差来源于下一层的残差的加权和。输出层的残差计算如下:
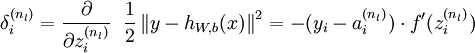
这个公式不做解释,可以查看公式来源,看斯坦福的深度学习教程的解释。
4.2 下一层为采样层(subsampling)的卷积层的残差
当一个卷积层L的下一层(L+1)为采样层,并假设我们已经计算得到了采样层的残差,现在计算该卷积层的残差。从最上面的网络结构图我们知道,采样层(L+1)的map大小是卷积层L的1/(scale*scale),ToolBox里面,scale取2,但这两层的map个数是一样的,卷积层L的某个map中的4个单元与L+1层对应map的一个单元关联,可以对采样层的残差与一个scale*scale的全1矩阵进行克罗内克积进行扩充,使得采样层的残差的维度与上一层的输出map的维度一致,Toolbox的代码如下,其中d表示残差,a表示输出值:
net.layers{l}.d{j} = net.layers{l}.a{j} .* (1 - net.layers{l}.a{j}) .* expand(net.layers{l + 1}.d{j}, [net.layers{l + 1}.scale net.layers{l + 1}.scale 1])
扩展过程:
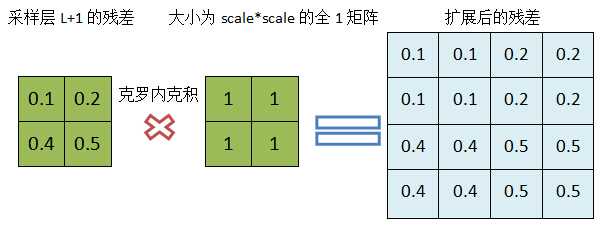
图5
利用卷积计算卷积层的残差:
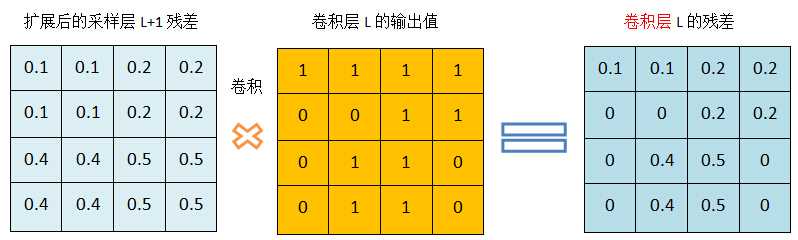
图6
4.3 下一层为卷积层(subsampling)的采样层的残差
当某个采样层L的下一层是卷积层(L+1),并假设我们已经计算出L+1层的残差,现在计算L层的残差。采样层到卷积层直接的连接是有权重和偏置参数的,因此不像卷积层到采样层那样简单。现再假设L层第j个map Mj与L+1层的M2j关联,按照BP的原理,L层的残差Dj是L+1层残差D2j的加权和,但是这里的困难在于,我们很难理清M2j的那些单元通过哪些权重与Mj的哪些单元关联,Toolbox里面还是采用卷积(稍作变形)巧妙的解决了这个问题,其代码为:
convn(net.layers{l + 1}.d{j}, rot180(net.layers{l + 1}.k{i}{j}), ‘full‘);
rot180表示对矩阵进行180度旋转(可通过行对称交换和列对称交换完成),为什么这里要对卷积核进行旋转,答案是:通过这个旋转,‘full‘模式下得卷积的正好抓住了前向传输计算上层map单元与卷积和及当期层map的关联关系,需要注意的是matlab的内置函数convn在计算卷积前,会对卷积核进行一次旋转,因此我们之前的所有卷积的计算都对卷积核进行了旋转:
a =
1 1 1
1 1 1
1 1 1
k =
1 2 3
4 5 6
7 8 9
>> convn(a,k,‘full‘)
ans =
1 3 6 5 3
5 12 21 16 9
12 27 45 33 18
11 24 39 28 15
7 15 24 17 9
convn在计算前还会对待卷积矩阵进行0扩展,如果卷积核为k*k,待卷积矩阵为n*n,需要以n*n原矩阵为中心扩展到(n+2(k-1))*(n+2(k-1)),所有上面convn(a,k,‘full‘)的计算过程如下:
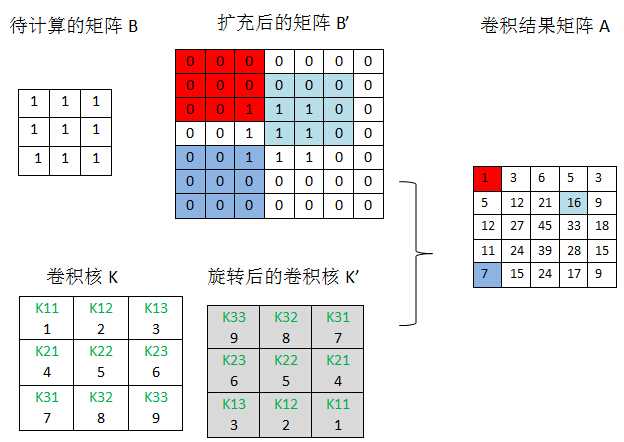
图7
实际上convn内部是否旋转对网络训练没有影响,只要内部保持一致(即都要么旋转,要么都不旋转),所有我的卷积实现里面没有对卷积核旋转。如果在convn计算前,先对卷积核旋转180度,然后convn内部又对其旋转180度,相当于卷积核没有变。
为了描述清楚对卷积核旋转180与卷积层的残差的卷积所关联的权重与单元,正是前向计算所关联的权重与单元,我们选一个稍微大一点的卷积核,即假设卷积层采用用3*3的卷积核,其上一层采样层的输出map的大小是5*5,那么前向传输由采样层得到卷积层的过程如下:
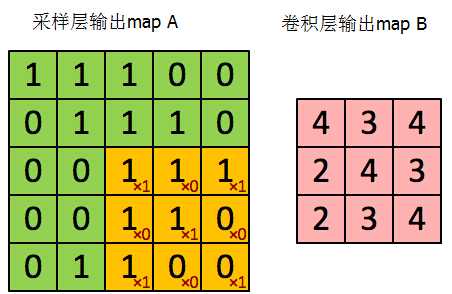
图8
这里我们采用自己实现的convn(即内部不会对卷积核旋转),并假定上面的矩阵A、B下标都从1开始,那么有:
B11 = A11*K11 + A12*K12 + A13*K13 + A21*K21 + A22*K22 + A23*K23 + A31*K31 + A32*K32 + A33*K33
B12 = A12*K11 + A13*K12 + A14*K13 + A22*K21 + A23*K22 + A24*K23 + A32*K31 + A33*K32 + A34*K33
B13 = A13*K11 + A14*K12 + A15*K13 + A23*K21 + A24*K22 + A25*K23 + A33*K31 + A34*K32 + A35*K33
B21 = A21*K11 + A22*K12 + A23*K13 + A31*K21 + A32*K22 + A33*K23 + A41*K31 + A42*K32 + A43*K33
B22 = A22*K11 + A23*K12 + A24*K13 + A32*K21 + A33*K22 + A34*K23 + A42*K31 + A43*K32 + A44*K33
B23 = A23*K11 + A24*K12 + A25*K13 + A33*K21 + A34*K22 + A35*K23 + A43*K31 + A44*K32 + A45*K33
B31 = A31*K11 + A32*K12 + A33*K13 + A41*K21 + A42*K22 + A43*K23 + A51*K31 + A52*K32 + A53*K33
B32 = A32*K11 + A33*K12 + A34*K13 + A42*K21 + A43*K22 + A44*K23 + A52*K31 + A53*K32 + A54*K33
B33 = A33*K11 + A34*K12 + A35*K13 + A43*K21 + A44*K22 + A45*K23 + A53*K31 + A54*K32 + A55*K33
我们可以得到B矩阵每个单元与哪些卷积核单元和哪些A矩阵的单元之间有关联:
A11 [K11] [B11]
A12 [K12, K11] [B12, B11]
A13 [K13, K12, K11] [B12, B13, B11]
A14 [K13, K12] [B12, B13]
A15 [K13] [B13]
A21 [K21, K11] [B21, B11]
A22 [K22, K21, K12, K11] [B12, B22, B21, B11]
A23 [K23, K22, K21, K13, K12, K11] [B23, B22, B21, B12, B13, B11]
A24 [K23, K22, K13, K12] [B23, B12, B13, B22]
A25 [K23, K13] [B23, B13]
A31 [K31, K21, K11] [B31, B21, B11]
A32 [K32, K31, K22, K21, K12, K11] [B31, B32, B22, B12, B21, B11]
A33 [K33, K32, K31, K23, K22, K21, K13, K12, K11] [B23, B22, B21, B31, B12, B13, B11, B33, B32]
A34 [K33, K32, K23, K22, K13, K12] [B23, B22, B32, B33, B12, B13]
A35 [K33, K23, K13] [B23, B13, B33]
A41 [K31, K21] [B31, B21]
A42 [K32, K31, K22, K21] [B32, B22, B21, B31]
A43 [K33, K32, K31, K23, K22, K21] [B31, B23, B22, B32, B33, B21]
A44 [K33, K32, K23, K22] [B23, B22, B32, B33]
A45 [K33, K23] [B23, B33]
A51 [K31] [B31]
A52 [K32, K31] [B31, B32]
A53 [K33, K32, K31] [B31, B32, B33]
A54 [K33, K32] [B32, B33]
A55 [K33] [B33]
然后再用matlab的convn(内部会对卷积核进行180度旋转)进行一次convn(B,K,‘full‘),结合图7,看红色部分,除去0,A11=B‘33*K‘33=B11*K11,发现A11正好与K11、B11关联对不对;我们再看一个A24=B‘34*K‘21+B‘35*K‘22+B‘44*K‘31+B‘45*K‘32=B12*K23+B13*K22+B22*K13+B23*K12,发现参与A24计算的卷积核单元与B矩阵单元,正好是前向计算时关联的单元,所以我们可以通过旋转卷积核后进行卷积而得到采样层的残差。
残差计算出来后,剩下的就是用更新权重和偏置,这和BP是一样的,因此不再细究。
/******************************************************************************************************/
当接在卷积层的下一层为pooling层时,求卷积层的误差敏感项
如果是mean-pooling就把误差也平均了传递到卷积层,如果是max-pooling就只对原convolution区块中输出最大值的那个neuron进行反向传播,其他neuron对权值更新的贡献算做0
这张图来自博客http://blog.csdn.net/wds555/article/details/44100581,总结得很好
<span style="font-size:14px;"><span style="font-size:18px;"><span style="font-size:18px;">"""This tutorial introduces the LeNet5 neural network architecture
using Theano. LeNet5 is a convolutional neural network, good for
classifying images. This tutorial shows how to build the architecture,
and comes with all the hyper-parameters you need to reproduce the
paper's MNIST results.
This implementation simplifies the model in the following ways:
- LeNetConvPool doesn't implement location-specific gain and bias parameters
- LeNetConvPool doesn't implement pooling by average, it implements pooling
by max.
- Digit classification is implemented with a logistic regression rather than
an RBF network
- LeNet5 was not fully-connected convolutions at second layer
References:
- Y. LeCun, L. Bottou, Y. Bengio and P. Haffner:
Gradient-Based Learning Applied to Document
Recognition, Proceedings of the IEEE, 86(11):2278-2324, November 1998.
http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf
"""
import os
import sys
import time
import numpy
import theano
import theano.tensor as T
from theano.tensor.signal import downsample
from theano.tensor.nnet import conv
from logistic_sgd import LogisticRegression, load_data
from mlp import HiddenLayer
class LeNetConvPoolLayer(object):
"""Pool Layer of a convolutional network """
def __init__(self, rng, input, filter_shape, image_shape, poolsize=(2, 2)):
"""
Allocate a LeNetConvPoolLayer with shared variable internal parameters.
:type rng: numpy.random.RandomState
:param rng: a random number generator used to initialize weights
:type input: theano.tensor.dtensor4
:param input: symbolic image tensor, of shape image_shape
:type filter_shape: tuple or list of length 4
:param filter_shape: (number of filters, num input feature maps,
filter height, filter width)
:type image_shape: tuple or list of length 4
:param image_shape: (batch size, num input feature maps,
image height, image width)
:type poolsize: tuple or list of length 2
:param poolsize: the downsampling (pooling) factor (#rows, #cols)
"""
assert image_shape[1] == filter_shape[1]
self.input = input
# there are "num input feature maps * filter height * filter width"
# inputs to each hidden unit
fan_in = numpy.prod(filter_shape[1:])
# each unit in the lower layer receives a gradient from:
# "num output feature maps * filter height * filter width" /
# pooling size
fan_out = (filter_shape[0] * numpy.prod(filter_shape[2:]) /
numpy.prod(poolsize))
# initialize weights with random weights
W_bound = numpy.sqrt(6. / (fan_in + fan_out))
self.W = theano.shared(
numpy.asarray(
rng.uniform(low=-W_bound, high=W_bound, size=filter_shape),
dtype=theano.config.floatX
),
borrow=True
)
# the bias is a 1D tensor -- one bias per output feature map
b_values = numpy.zeros((filter_shape[0],), dtype=theano.config.floatX)
self.b = theano.shared(value=b_values, borrow=True)
# convolve input feature maps with filters
conv_out = conv.conv2d(
input=input,
filters=self.W,
filter_shape=filter_shape,
image_shape=image_shape
)
# downsample each feature map individually, using maxpooling
pooled_out = downsample.max_pool_2d(
input=conv_out,
ds=poolsize,
ignore_border=True
)
# add the bias term. Since the bias is a vector (1D array), we first
# reshape it to a tensor of shape (1, n_filters, 1, 1). Each bias will
# thus be broadcasted across mini-batches and feature map
# width & height
self.output = T.tanh(pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))
# store parameters of this layer
self.params = [self.W, self.b]
def evaluate_lenet5(learning_rate=0.1, n_epochs=200,
dataset='mnist.pkl.gz',
nkerns=[20, 50], batch_size=500):
""" Demonstrates lenet on MNIST dataset
:type learning_rate: float
:param learning_rate: learning rate used (factor for the stochastic
gradient)
:type n_epochs: int
:param n_epochs: maximal number of epochs to run the optimizer
:type dataset: string
:param dataset: path to the dataset used for training /testing (MNIST here)
:type nkerns: list of ints
:param nkerns: number of kernels on each layer
"""
rng = numpy.random.RandomState(23455)
datasets = load_data(dataset)
train_set_x, train_set_y = datasets[0]
valid_set_x, valid_set_y = datasets[1]
test_set_x, test_set_y = datasets[2]
# compute number of minibatches for training, validation and testing
n_train_batches = train_set_x.get_value(borrow=True).shape[0]
n_valid_batches = valid_set_x.get_value(borrow=True).shape[0]
n_test_batches = test_set_x.get_value(borrow=True).shape[0]
n_train_batches /= batch_size
n_valid_batches /= batch_size
n_test_batches /= batch_size
# allocate symbolic variables for the data
index = T.lscalar() # index to a [mini]batch
# start-snippet-1
x = T.matrix('x') # the data is presented as rasterized images
y = T.ivector('y') # the labels are presented as 1D vector of
# [int] labels
######################
# BUILD ACTUAL MODEL #
######################
print '... building the model'
# Reshape matrix of rasterized images of shape (batch_size, 28 * 28)
# to a 4D tensor, compatible with our LeNetConvPoolLayer
# (28, 28) is the size of MNIST images.
layer0_input = x.reshape((batch_size, 1, 28, 28))
# Construct the first convolutional pooling layer:
# filtering reduces the image size to (28-5+1 , 28-5+1) = (24, 24)
# maxpooling reduces this further to (24/2, 24/2) = (12, 12)
# 4D output tensor is thus of shape (batch_size, nkerns[0], 12, 12)
layer0 = LeNetConvPoolLayer(
rng,
input=layer0_input,
image_shape=(batch_size, 1, 28, 28),
filter_shape=(nkerns[0], 1, 5, 5),
poolsize=(2, 2)
)
# Construct the second convolutional pooling layer
# filtering reduces the image size to (12-5+1, 12-5+1) = (8, 8)
# maxpooling reduces this further to (8/2, 8/2) = (4, 4)
# 4D output tensor is thus of shape (batch_size, nkerns[1], 4, 4)
layer1 = LeNetConvPoolLayer(
rng,
input=layer0.output,
image_shape=(batch_size, nkerns[0], 12, 12),
filter_shape=(nkerns[1], nkerns[0], 5, 5),
poolsize=(2, 2)
)
# the HiddenLayer being fully-connected, it operates on 2D matrices of
# shape (batch_size, num_pixels) (i.e matrix of rasterized images).
# This will generate a matrix of shape (batch_size, nkerns[1] * 4 * 4),
# or (500, 50 * 4 * 4) = (500, 800) with the default values.
layer2_input = layer1.output.flatten(2)
# construct a fully-connected sigmoidal layer
layer2 = HiddenLayer(
rng,
input=layer2_input,
n_in=nkerns[1] * 4 * 4,
n_out=500,
activation=T.tanh
)
# classify the values of the fully-connected sigmoidal layer
layer3 = LogisticRegression(input=layer2.output, n_in=500, n_out=10)
# the cost we minimize during training is the NLL of the model
cost = layer3.negative_log_likelihood(y)
# create a function to compute the mistakes that are made by the model
test_model = theano.function(
[index],
layer3.errors(y),
givens={
x: test_set_x[index * batch_size: (index + 1) * batch_size],
y: test_set_y[index * batch_size: (index + 1) * batch_size]
}
)
validate_model = theano.function(
[index],
layer3.errors(y),
givens={
x: valid_set_x[index * batch_size: (index + 1) * batch_size],
y: valid_set_y[index * batch_size: (index + 1) * batch_size]
}
)
# create a list of all model parameters to be fit by gradient descent
params = layer3.params + layer2.params + layer1.params + layer0.params
# create a list of gradients for all model parameters
grads = T.grad(cost, params)
# train_model is a function that updates the model parameters by
# SGD Since this model has many parameters, it would be tedious to
# manually create an update rule for each model parameter. We thus
# create the updates list by automatically looping over all
# (params[i], grads[i]) pairs.
updates = [
(param_i, param_i - learning_rate * grad_i)
for param_i, grad_i in zip(params, grads)
]
train_model = theano.function(
[index],
cost,
updates=updates,
givens={
x: train_set_x[index * batch_size: (index + 1) * batch_size],
y: train_set_y[index * batch_size: (index + 1) * batch_size]
}
)
# end-snippet-1
###############
# TRAIN MODEL #
###############
print '... training'
# early-stopping parameters
patience = 10000 # look as this many examples regardless
patience_increase = 2 # wait this much longer when a new best is
# found
improvement_threshold = 0.995 # a relative improvement of this much is
# considered significant
validation_frequency = min(n_train_batches, patience / 2)
# go through this many
# minibatche before checking the network
# on the validation set; in this case we
# check every epoch
best_validation_loss = numpy.inf
best_iter = 0
test_score = 0.
start_time = time.clock()
epoch = 0
done_looping = False
while (epoch < n_epochs) and (not done_looping):
epoch = epoch + 1
for minibatch_index in xrange(n_train_batches):
iter = (epoch - 1) * n_train_batches + minibatch_index
if iter % 100 == 0:
print 'training @ iter = ', iter
cost_ij = train_model(minibatch_index)
if (iter + 1) % validation_frequency == 0:
# compute zero-one loss on validation set
validation_losses = [validate_model(i) for i
in xrange(n_valid_batches)]
this_validation_loss = numpy.mean(validation_losses)
print('epoch %i, minibatch %i/%i, validation error %f %%' %
(epoch, minibatch_index + 1, n_train_batches,
this_validation_loss * 100.))
# if we got the best validation score until now
if this_validation_loss < best_validation_loss:
#improve patience if loss improvement is good enough
if this_validation_loss < best_validation_loss * improvement_threshold:
patience = max(patience, iter * patience_increase)
# save best validation score and iteration number
best_validation_loss = this_validation_loss
best_iter = iter
# test it on the test set
test_losses = [
test_model(i)
for i in xrange(n_test_batches)
]
test_score = numpy.mean(test_losses)
print((' epoch %i, minibatch %i/%i, test error of '
'best model %f %%') %
(epoch, minibatch_index + 1, n_train_batches,
test_score * 100.))
if patience <= iter:
done_looping = True
break
end_time = time.clock()
print('Optimization complete.')
print('Best validation score of %f %% obtained at iteration %i, '
'with test performance %f %%' %
(best_validation_loss * 100., best_iter + 1, test_score * 100.))
print >> sys.stderr, ('The code for file ' +
os.path.split(__file__)[1] +
' ran for %.2fm' % ((end_time - start_time) / 60.))
if __name__ == '__main__':
evaluate_lenet5()
def experiment(state, channel):
evaluate_lenet5(state.learning_rate, dataset=state.dataset)</span></span></span>标签:
原文地址:http://blog.csdn.net/u014568921/article/details/45222623