标签:
这次主要想写两篇,一篇把决策树的相关思想和方法解释清楚,另外一个说一下ensemble形式的决策树,random forest,依据主要是breiman的论文。
这篇讲决策树(主要以cart为例,因为random forest的大多实现也是根据cart)
1、cart的生成。
cart的全称是classification and regression tree,意为分类回归树。也就是说这类决策树既可以解决分类问题,也能解决回归问题。因此针对分类树和回归树,cart有两种生成方式。这里要注意,树是根据训练集数据依据一定的规则生成,对于测试集数据,只需要将数据从根节点输入,像流水一样,沿着应该走的管道,到达所预测的类别或者回归数值。
针对任何一种机器学习模型,其训练过程都大同小异,目的都是为了使训练集数据尽可能被较好地分类和拟合。cart也不例外,无论是分类树还是回归树,无外乎都需要在生成过程(训练过程)使得某些误差最小,最恰当的安排训练数据。下面分别说明。
(1)分类树的生成。
对于一份lable为分类变量的训练集,存在一个指标叫做基尼指数,只需要知道基尼指数是概率分布的其中一种表示
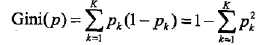
pk表示某一类别的样本数占总样本数的比例。再说一次,只要是分类性质的样本集,本身就存在基尼指数这个属性。
然后就是到底按照哪个特征的哪个值进行二分训练集,注意,cart树的每一步都是二分,没有多分情况。
![]()
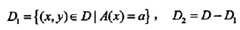
没有简单的办法,只有穷举,用每个特征(这里是A)的每个可能的值(这里是a)进行二分,每分一次就会产生两份样本,然后按照上式求每一次的综合基尼指数,最后选择基尼指数最小的那个分法就好了。为什么选择最小的呢?我们看看基尼指数的含义,实质上表示的是一份样本集的纯净程度,拿二分类类型的样本集来说,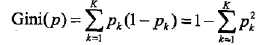 这个算式在什么情况下最大?最小?当所有样本都是一类的时候,最小,为0;当一半一半时,最大,为2*0.5^2。所以,越小的基尼指数,意味着这次二分最大程度保证了分开的两份样本集各自的纯净度,这也正是我们想要的。
这个算式在什么情况下最大?最小?当所有样本都是一类的时候,最小,为0;当一半一半时,最大,为2*0.5^2。所以,越小的基尼指数,意味着这次二分最大程度保证了分开的两份样本集各自的纯净度,这也正是我们想要的。
2、回归树的生成
对应与分类树的最小化基尼指数准则,回归树该怎么确定哪个分法才最好呢?最小二乘!经典的最小二乘算法!
对于每一个特征的每一个值,我们依然都尝试一遍,每一次,都算一下5.21式。c1,c2分别是分开的两份样本的各自均值,也就是能使拟合误差最小的预测值。直至满足停止条件。

(3)关于停止条件。
对于分类回归树来说,停止条件可以有多种,也可以人为设定。比如对于分类树,可以当所有特征都用尽时停止,也可以当某个树杈包含的所有样本都纯净时停止。对于回归树,可以认为设定当某个树杈包含的样本个数或者方差小于某个阈值时停止。
2、cart的剪枝以及其它的剪枝算法。
这里介绍两种主要的剪枝算法--reduced error prune and cost complexity prune(ccp)
插一句,为什么要剪枝。可以想象一下,对于决策树来说,它可以把训练集训练的100%准确,就是完全拟合,但是对于任何新的数据,它会产生巨大的误差。因此一颗生长完全的决策树其实是overfitting的,必须要通过剪枝来降低它的泛化误差。
另外,剪枝算法通常都需要有验证集数据的帮助。
(1)reduced error prune
这种剪枝算法是最简单最直观的。它完全脱离训练集数据,采用新的验证集数据去判断某一个subtree该不该替换成leaf。首先,先用完整的未剪枝的树把验证集测试一遍,肯定有很多错误。这时候,针对每一个node,都试着剪掉一遍,然后每剪掉一个node,都再测试一遍,看看是否提高了准确度,最终选择那个提高准确度最高的node,剪掉它。这叫做一轮剪枝,然后继续重复,每次剪一个node,直到准确度不再有提高为止。
(2)ccp
这种剪枝算法就是cart树使用的。
这种算法并没有完全脱离训练集。第一步先依据训练集,尝试剪掉每个节点(有歧义,其实是每次只剪一个,比如节点A,B,C,先剪掉A,保留B,C;再剪掉B,保留A,C....)
在训练集上计算以下指标a:

取最小的那个a对应的节点,剪掉!,这时候生成了第一个子树(N-1个节点,原树N个)。重复以上步骤,直到最后只剩下根节点,作为最后一个子树。
这时候,我们有了一系列的子树,然后第二步:
验证集登场,这时候,只需要使用验证集对所有子树走一遍,取误差最小的那棵树,就是我们最终需要的树!
可以看出,这个指标a,既联系了tree size,又联系了error,最终的optimal a相当于一定程度上给决策树加上了复杂度的惩罚项,也就是做了相应的正则化。既减少了误差,又平衡了复杂度。
好了,大概就是这些!
下一次写一点random forest。
标签:
原文地址:http://www.cnblogs.com/lvlvlvlvlv/p/5856986.html