标签:
卡特兰数是组合数学中常见也是重要的特殊计数公式。
首先给出一个现实问题的模型:
给出凸多边形的边数n,求解该凸多边形内部不相交的对角线把这个区域分成三角形区域的方法数。

首先我们进行初步的分析,当n=2,h2=1,也就是说对于三角形,划分的情况数是1.这似乎有些不好理解,由于三角形内部无法添加对角线,所以符合情况的就是三角形本身,情况数为1.
下面我们讨论n取任意值的情况。
看下面的图。
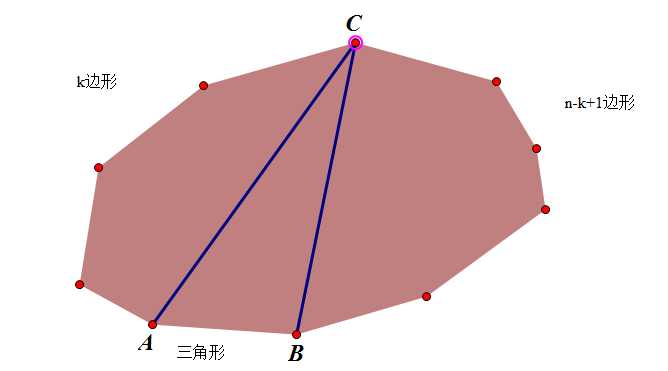
考虑将n+1凸边形的子问题,即我们将AB视为基边,枚举C的位置,有n-1个可枚举位置,然后结合基本的计数原理,我们能够看到下面的递推式能够不重不漏的表示出h[n].
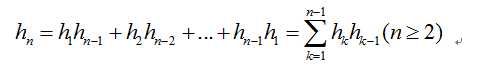
而现在的问题在于,这样的递推公式是我们不喜爱的,我们喜欢的形式是斐波那契数列,给出的是前后项的关系式然后我们可以在线性时间复杂度下求出该数列,那么下面我们需要讨论的便是如何得到这个递推公式的解。



下面是根据这条结论计算卡特兰数列的JAVA代码:
import java.io.*; import java.util.*; import java.math.BigInteger; public class Main { public static void main(String args[]) { BigInteger[] a = new BigInteger[101]; a[0] = BigInteger.ZERO; a[1] = BigInteger.valueOf(1); for(int i = 2; i <= 100; ++i) a[i] = a[i - 1].multiply(BigInteger.valueOf(4 * i - 2)).divide(BigInteger.valueOf(i+1)); Scanner in = new Scanner(System.in); int n; while(in.hasNext()) { n = in.nextInt(); System.out.println(a[n]); } } }
标签:
原文地址:http://www.cnblogs.com/rhythmic/p/5857927.html