浅谈数据结构-堆

标签：

在数据结构的世界中有一个叫堆的玩意，这玩意有什么用呢？无用，都去pq了 堆，其实就是一棵完全二叉树。

“若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树”  by 谋财害命公司 百度

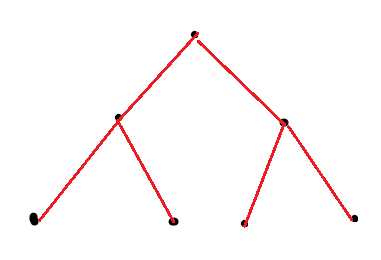
↑清真的 完全二叉树 ↓

啊那么为什么会闲的无聊出现这种奇怪的数据结构呢？

因为我们的某些算法可能需要堆来进行优化，如dj，prim。

堆可以在O（1）的时间取出最优值，但是需要O（logn）的时间修改和O（nlogn）的时间建立。【啊大概好像也许应该可能是这样的复杂度】

那么我们该怎么建立一个清真的堆呢？

首先我们要明白堆的原理：

1.加入元素时，在尾部添加，然后从尾部开始递归，爬树爬到顶端，在爬树的过程中进行交换最优值的操作。

2.删除元素时，先把第一个元素和末尾元素的值换一下，然后删除末尾元素，从根节点往下递归，直到叶子节点，递归过程进行最优值交换操作。

3.查询元素时，查第一个元素。

↑啊这是不是非常简单啊？pj选手不会的都拉出去续了

相信有些人可能看了上面这三段我意念出来的文字，像便秘一样写不出来，唉我只好舍命陪君子瞎jb口胡着写一个啦~~~喵！

【我以堆排序为例子】

1 void  put(int k)
2 {
3     int father=k>>1;
4     if (k==0) return ;
5     if (a[k]<a[father])
6       swap(a[k],a[father]),put(father);
7     return ;
8 }

FA♂Q

 1 void del(int k)
 2 {
 3     int lc,rc;
 4     lc=k<<1;
 5     rc=(k<<1)+1;
 6     if (lc>len && rc>len) 
 7       return ;
 8     if (lc<=len && rc>len)
 9       if (a[k]>a[lc])
10         {
11             swap(a[k],a[lc]);
12             return ;
13         }
14     if (lc<=len && rc<=len)
15        {
16           int tc=rc;
17           if (a[lc]<a[rc]) tc=lc;
18           if (a[k]>a[tc])
19             swap(a[k],a[tc]),del(tc);
20        }
21 }

Change♂boss♂of♂this♂gym

YY了一下插入和删除这两个操作，大概也许应该是没错的

然后就可以用heap做许多好玩的事情啦（误）

浅谈数据结构-堆

标签：

原文地址：http://www.cnblogs.com/yz12138/p/5869601.html