标签:
朴素贝叶斯是基于贝叶斯定理与特征条件独立假设的分类方法。实现简单、学习和预测的效率都很高,是一种常用的分类方法。贝叶斯分类器是一个统计分类器。它们能够预测类别所属的概率。接下来将介绍贝叶斯定理和特征条件独立假设。
条件概率:若Ω是全集,A、B是其中的事件(子集),P表示事件发生的概率,则
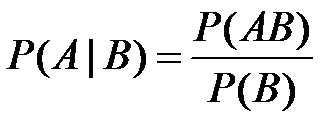
为事件B发生后A发生的概率。
乘法定理:设A1,A2,…,An为n个事件,n≥2,且P(A1A2…A(n-1))>0,则有
P(A1A2…An)=P(An|A12…A(n-1)) P(A(n-1)|A12…A(n-2))…·P(A2|A1)P(A1)。
全概率公式:若事件B1,B2,…构成一个完备事件组且都有正概率,则对任意一个事件A,有如下公式成立:
P(A)=P(AB1)+P(AB2)+...+P(ABn)=P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn).此公式即为全概率公式。
由以往的数据分析得到的概率, 叫做先验概率.
而在得到信息之后再重新加以修正的概率叫做后验概率.
P(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
P(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
定义:设X是类标号未知的数据样本。设H为某种假定,如数据样本X属于某特定的类C。对于分类问题,我们希望确定P(H|X),即给定观测数据样本X,假定H成立的概率。贝叶斯定理给出了如下计算P(H|X)的简单有效的方法:
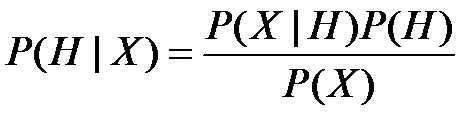
P(H)是先验概率,或称H的先验概率。P(X|H)代表假设H成立的情况下,观察到X的概率。
P(H| X )是后验概率,或称条件X下H的后验概率。
先验概率泛指一类事物发生的概率,通常根据历史资料或主观判断,未经实验证实所确定的概率。而后验概率涉及的是某个特定条件下一个具体的事物发生的概率
用于分类的特征在类确定的条件下都是条件独立的。这一假设会使贝叶斯法变得简单,但有时会牺牲一定的分类准确率。
对于给定的训练数据集,首先基于特征条件独立假设学习输入输出的联合概率分布,然后基于此模型,对于给定的输入X,利用贝叶斯定理求出后验概率最大的输出y。
朴素贝叶斯分类的工作过程如下:
(1) 每个数据样本用一个n维特征向量X= {x1,x2,……,xn}表示,分别描述对n个属性A1,A2,……,An样本的n个度量。
(2) 假定有m个类C1,C2,…,Cm,给定一个未知的数据样本X(即没有类标号),分类器将预测X属于具有最高后验概率(条件X下)的类。也就是说,朴素贝叶斯分类将未知的样本分配给类Ci(1≤i≤m)当且仅当P(Ci|X)> P(Cj|X),对任意的j=1,2,…,m,j≠i。这样,最大化P(Ci|X)。其P(Ci|X)最大的类Ci称为最大后验假定。根据贝叶斯定理
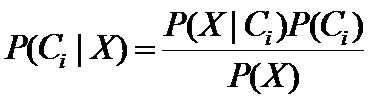
(3) 由于P(X)对于所有类为常数,只需要P(X|Ci)*P(Ci)最大即可。
如果Ci类的先验概率未知,则通常假定这些类是等概率的,即P(C1)=P(C2)=…=P(Cm),因此问题就转换为对P(X|Ci)的最大化(P(X|Ci)常被称为给定Ci时数据X的似然度,而使P(X|Ci)最大的假设Ci称为最大似然假设)。否则,需要最大化P(X|Ci)*P(Ci)。注意,类的先验概率可以用P(Ci)=si/s计算,其中si是类Ci中的训练样本数,而s是训练样本总数。
(4) 给定具有许多属性的数据集,计算P(X|Ci)的开销可能非常大。为降低计算P(X|Ci)的开销,可以做类条件独立的朴素假定。
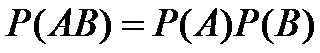
给定样本的类标号,假定属性值相互条件独立,即在属性间,不存在依赖关系。这样
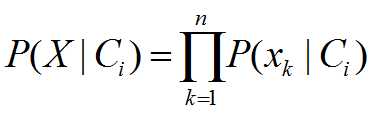
(5) 对未知样本X分类,也就是对每个类Ci,计算P(X|Ci)*P(Ci)。
样本X被指派到类Ci,当且仅当P(Ci|X)> P(Cj|X),1≤j≤m,j≠i,换言之,X被指派到其P(X|Ci)*P(Ci)最大的类。
标签:
原文地址:http://www.cnblogs.com/douza/p/5871017.html