标签:
题意:假设有n个人按顺序的身高分别是h[1], h[2] ... h[n],从中挑出一些人形成一个新的队形,新的队形若满足以下要求,则就是新的完美队形:
1、连续的
2、形成回文串
3、从左到中间那个人,身高需保证不下降
问有组成完美队形的最多人数
题解:Manacher算法的变形。
首先我们来解释一下Manacher算法:在我看来就是一个优化的暴力。
我们首先统一奇偶回文串成为奇数回文串,就是在两个数之间加入一些不可能出现的数。
例如题目:1 2 3 3 2 5 2 3 1—>(符号更加清楚)$ # 1 # 2 # 3 # 3 # 2 # 5 # 2 # 3 # 1 # &(其中首尾多的#保证答案正确) ,注意首尾多增加 & 与 $ 为了不处理边界。接着我们只需要统计此时回文串长度的一半(包括中间一个字符)再减一就是此处总回文串的长度。
首先使用dp数组记录回文串一半长度,id记录最大dp的下标,maxid记录最大dp可以管到的最后一个距离,然后利用回文串的性质减少每次比较的次数
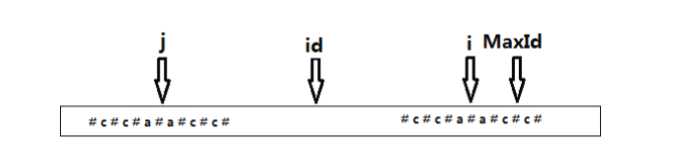
如图:在不超过maxid的位置(超过就不确定是否匹配成功了)j(i相对于id的对应位置)可以直接赋值给i,接着i再暴力寻找回文串是否没有找完整。最后我们的变形就在暴力处增加判断就好
#include<set> #include<map> #include<queue> #include<stack> #include<cmath> #include<vector> #include<string> #include<cstdio> #include<cstring> #include<stdlib.h> #include<iostream> #include<algorithm> using namespace std; #define eps 1E-8 /*注意可能会有输出-0.000*/ #define Sgn(x) (x<-eps? -1 :x<eps? 0:1)//x为两个浮点数差的比较,注意返回整型 #define Cvs(x) (x > 0.0 ? x+eps : x-eps)//浮点数转化 #define zero(x) (((x)>0?(x):-(x))<eps)//判断是否等于0 #define mul(a,b) (a<<b) #define dir(a,b) (a>>b) typedef long long ll; typedef unsigned long long ull; const int Inf=1<<28; const double Pi=acos(-1.0); const int Mod=1e9+7; const int Max=300010; int num[Max]; int Init(int n)//增加其他字符,让奇数偶数回文串都变成奇数回文串 { for(int i=n-1;i>=0;--i) { num[(i<<1)+2]=num[i]; num[(i<<1)|1]=0;//不可能出现的字符 } num[(n<<1)|1]=0; num[0]=1;//边界 num[(n<<1)+2]=2; return (n<<1)+3; } int dp[Max];//每个位置匹配长度 int Manacher(int n) { int manx=0; int id=0,maxid=0; dp[0]=1; for(int i=1;i<n;++i) { if(maxid>=i) dp[i]=min(dp[(id<<1)-i],maxid-i+1); else dp[i]=1; while(num[i+dp[i]]==num[i-dp[i]]&&(num[i+dp[i]]==0||num[i+dp[i]]<=num[i+dp[i]-2]))//注意这儿需要修改 dp[i]++; if(maxid<i+dp[i]-1) { maxid=i+dp[i]-1; id=i; } if(manx<dp[i]-1) manx=dp[i]-1; } return manx; } int main() { int t,n; scanf("%d",&t); while(t--) { scanf("%d",&n); for(int i=0;i<n;++i) scanf("%d",&num[i]); n=Init(n); printf("%d\n",Manacher(n)); } return 0; }
HDU 4513 吉哥系列故事——完美队形II (Manacher变形)
标签:
原文地址:http://www.cnblogs.com/zhuanzhuruyi/p/5873869.html