标签:
1、已知函数 $f(x)$ 的定义域为 $[-1, 1]$, 求 $f(ax) + f\left(\displaystyle{x\over a}\right)$ 的定义域, 其中 $a > 0$.
解答:
仿照例4解法易知其定义域为 $$\begin{cases}[-a, a],\ (0 < a < 1)\\ \left[-\displaystyle{1\over a}, {1\over a}\right],\ (a \ge 1) \end{cases}.$$
2、函数 $f$ 定义在整数集上, 满足 $$f(n) = \begin{cases}n - 3,\ (n \ge 1000),\\ f\left(f(n + 5)\right),\ (n < 1000). \end{cases}$$ 求 $f(84)$.
解答:
参考例6, 例10解法, 考虑寻求规律.
令 $f_1(n) = f(n)$, $f_{m+1}(n) = f_m(f(n))$, 其中 $m = 1, 2, \cdots$. 则有$$f(84) = f_2(84+5) = f_3(84 + 2\times 5) = \cdots = f_{184}(84 + 183 + 5) = f_{184}(999).$$ 此后试解发现形成反复, 因此考虑寻找循环节. $$f_{n+2}(999) = f_{n+3}(1004) = f_{n+2}(1001) = f_{n+1}(998) = f_{n+2}(1003)$$ $$= f_{n+1}(1000) = f_{n}(997) = f_{n+1}(1002) = f_{n}(999).$$ 由此可得 $$f(84) = f_{184}(999) = f_{182}(999) = \cdots = f_2(999) = f_3(1004)$$ $$= f_2(1001) = f(998) = f_2(1003) = f(1000) = 997.$$
3、已知关于$x$的方程$|(x - 1)(x - 3)| = mx$有4个不同的实根. 求$m$的范围.
解答:
考虑图像法解决之.
令 $f(x) = |(x - 1)(x - 3)|$, $g(x) = mx$.
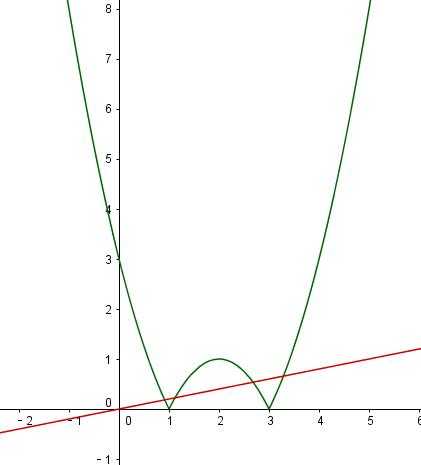
当 $g(x)$ 与上图中间部分相切时为最大值位置(切点位于第一象限), 即 $$mx = -(x - 1)(x - 3)$$ 之判别式为0时 $m$ 之取值: $$\Delta = (m - 4)^2 - 12 = 0\Rightarrow m = 4\pm2\sqrt3.$$ 验证可知, 当 $m = 4 - 2\sqrt3$ 时交点位于第一象限.
因此 $m\in\left(0,\ 4-2\sqrt3\right)$.
4、是否存在函数 $f: \mathbf{R}\rightarrow\mathbf{R}$, 使得对所有的实数 $x$, 都有 $f\left(x^2\right) - f^2(x) \ge \displaystyle{1\over 4}$. 并且对不同的 $x\in\mathbf{R}$, $f(x)$ 也不同.
解答:
由已知表达式 $f\left(x^2\right) - f^2(x) \ge \displaystyle{1\over 4}$ 考虑配方.
令 $x = 0, 1$ 分别得 $$f(0) - f^2(0) \ge {1\over4}\Rightarrow \left(f(0) - {1\over2}\right)^2 \le0\Rightarrow f(0) = {1\over2},$$ $$f(1) - f^2(1) \ge {1\over4}\Rightarrow \left(f(1) - {1\over2}\right)^2 \le0\Rightarrow f(1) = {1\over2},$$ 即有 $f(0) = f(1)$. 矛盾! 因此不存在.
5、函数 $f(x)$ 定义在 $[0, 1]$ 上, 且 $f(0) = f(1)$. 如果对不同的 $x_1, x_2\in[0, 1]$, 都有 $|f(x_1) - f(x_2)| < |x_1 - x_2|$, 证明: $|f(x_1) - f(x_2)| < \displaystyle{1\over2}$.
证明:
易知若 $0 \le x_1 < x_2\le 1$ 且 $0 < x_2 - x_1 \le \displaystyle{1\over2}$, 则有 $$|f(x_1) - f(x_2)| < |x_1 - x_2| \le {1\over2}.$$ 由此只需证明 $\displaystyle{1\over2} < x_2 - x_1 \le 1$ 时不等式亦成立即可: $$|f(x_1) - f(x_2)| = |f(x_2) - f(x_1) - f(1) + f(0)| \le |f(x_2) - f(1)| + |f(0) - f(x_1)|$$ $$< |x_2 - 1| + |0 - x_1| = 1 - x_2 + x_1 - 0 = 1 - (x_2 - x_1) < {1\over2}.$$ Q.E.D.
6、已知函数$y = f(x)$在其定义域上是增函数. 求证:
1. $y = f^{-1}(x)$在其定义域上也是增函数;
2. 若 $f(x)\equiv f^{-1}(x)$, 则在其定义域上 $f(x) = x$.
证明:
1. 此即证明当 $y_1 < y_2$ 时, 必有 $x_1 < x_2$. 需注意该函数存在反函数, 因此必为一一映射.
设 $f(x)$ 定义域为 $X$, 值域为 $Y$. 设 $y_1, y_2\in Y$ 且 $y_1 < y_2$. $\exists$ 惟一之 $x_1, x_2\in X$, 使得 $x_1 = f^{-1}(y_1)$, $x_2 = f^{-1}(y_2)$, 即 $f(x_1) = y_1$, $f(x_2) = y_2$. 由原函数单调性可知 $x_1 < x_2$, 故 $y = f^{-1}(x)$ 亦为增函数.
2. 若 $x < f(x)$ 且 $x\in X$, 则有 $$x < f(x) = f^{-1}(x)\Rightarrow f(x) < f^{-1}(f(x)) = x,$$ 矛盾! 同理可证明 $x > f(x)$时仍不成立.
Q.E.D.
扫描关注“奥数学苑”微信公众号(ID: aoshu_xueyuan)

数学奥林匹克问题解答:目标2017高中数学联赛基础班-2作业题解答-1
标签:
原文地址:http://www.cnblogs.com/zhaoyin/p/5874791.html