字符串之间的编辑距离

标签：

问题一：字符串s1与字符串s2之间的编辑距离为：将s1转换成s2的最少步数，转换过程可以进行的操作有：

1.插入一个字符

2.删除一个字符

3.替换一个字符

我们用f[i][j]表示s1[0,i]前i个字符组成的字符串，和s2[0,j]前j个字符组成的字符串，之间的编辑距离。若s[i-1]==s[j-1]，那么f[i][j]=f[i-1][j-1]，若s[i-1]！=s[j-1]，那么可以进行操作1，向s1中插入一个字符，则f[i][j]=f[i][j-1]+1，若进行操作2，向s1中删除一个字符，则f[i][j]=f[i-1][j]+1，若进行操作3，进行字符替换，则f[i][j]=f[i-1][j-1]+1。

int editdis(char *s1,char *s2)
{
    
    int m=strlen(s1);
    int n=strlen(s2);
    vector<vector<int>> f(m+1,vector<int>(n+1));
    for(int i=0;i<=m;i++)
    {
        f[i][0]=i;
    }
    for(int j=0;j<=n;j++)
        f[0][j]=j;
    for(int i=1;i<=m;i++)
        for(int j=1;j<=n;j++)
        {
            f[i][j]=s1[i-1]==s2[j-1]?f[i-1][j-1]:min(f[i-1][j],min(f[i][j-1],f[i-1][j-1]))+1;
        }
    return f[m][n];

}

问题二：字符串插入，判断字符串s3能否由s1和s2组成。

用f[i][j]表示s1[0~i]前i个字符串与s2[0~j]前j个字符串能否组成s3[0~i+j]。

字符串之间的编辑距离

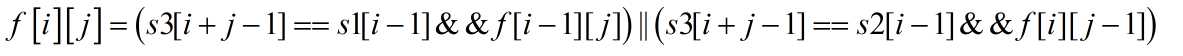
标签：

原文地址：http://www.cnblogs.com/beaglebone/p/5877613.html