标签:
多元线性回归模型用途:
1、 回归用来拟合,解释现象;
2、 用来构建观测数据集与自变量之间一个预测模型;
3、 用来量化y与 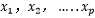 相关性强度
相关性强度
假设:
1、 观测数据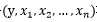 相互独立
相互独立
2、 随机误差服从于方差相同的正态分布
原理:

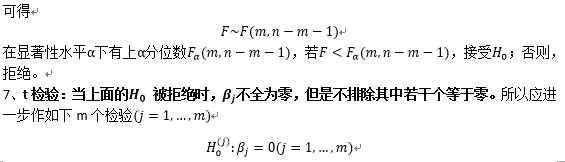


####R语言####################
1、#########################查看数据相关性######################################
data=iris
round(cor(data[,1:4]),3)
plot(data$x1,data$x2)
2、#########################初步建模##########################################
lm1=lm(y~x1+x2+x3,data=a1)
Summary(lm1)
通过F检验,发现初步建模的模型是否线性关系显著。从T检验发现,看哪几个自变量与因变量线性关系较为显著(注意,并不是说其余字段可以剔除)。
3、#######################模型诊断,即显著性检验##############################
par(mfrow=c(2,2)) ####设置画图为2*2的格式
plot(lm1,which=c(1;4)) ########画出lm1中对应于模型检验的4张图,包括残差图(自变量随机误差项是否同方差) 、QQ图(检验随机误差项是否正态分布)和Cook距离图(检验异常值)
a1=a1(-47)#########如有异常值,应以剔除
################################剔除后看效果############################
Lm2=lm(y~x1+x2+x3,data=a1)
Summary(lm2)
4、####################检验自变量多重共线性##################################
#####################方差膨胀因子检验:VIF###########################
Library(car)
Round(vif(lm2),2)
####################AIC和BIC选择#########################
Lm.aic=step(lm2,trace=F)
Summary(lm.aic)
Lm.bic=step(lm2,k=log(length(a1[,1])),trace=F)
Summary(lm.bic)
5、##############################模型效果#######################################
Y1=predict(lm2,a2)
Y2= predict(lm.aic,a2)
Y2= predict(lm.bic,a2)
Y0=a2[,10]
R0=y0-a2$ROEt
R1=y0-y1
R2=y0-y2
R3=y0-y3
Resid=abs(as.data.frame(cbind(r0,r1,r2,r3)))
Sampply(resid,mean)
#########matlab语言########################
1、 b=regress(Y,X),b 为回归系数估计值
2、 [b,bint,r,rint,stats]=regress(Y,X,alpha)
alpha 为显著性水平(缺省时设定为0.05),b,bint 为回归系数估计值和它们的置信区间,r,rint 为残差(向量)及其置信区间,stats 是用于检验回归模型的统 计量,有四个数值,第一个是 ,第二个是F,第三个是与F 对应的概率p, 拒绝,回归模型成立,第四个是残差的方差
3、 残差及其置信区间可以用 rcoplot(r,rint)画图
#######################查看除第?个数据外其余残差的置信区间均包含零点,即视为异常点,将其剔除后重新计算###########################
4、########################实现变量选择##############################
stepwise(x,y,inmodel,alpha) 其中x是自变量数据,y是因变量数据,分别为 m n× 和 1 ×n 矩阵,inmodel是矩阵x的 列数的指标,给出初始模型中包括的子集(缺省时设定为空),alpha为显著性水平。
标签:
原文地址:http://www.cnblogs.com/dudumiaomiao/p/5878087.html