标签:
前提条件是这样的:输入一个图(可以是有向图,也可以是无向图,允许平行边存在),我们要做的事情是将这个图切割成两个子图,(切割的定义:将图中的所有顶点分为两个集合A和B,要求这两个集合非空)假设这个图中的顶点数为n,边的条数为m,这样一来就总共有2的n次方减2种切割方案,(每个顶点有两种选择,要么选集合A,要么选集合B,同时保证两个集合非空),要找到一种切割方案,使得切割经过的边最少(仅仅指从左边的集合A到右边的集合B的边,忽略有向图中从右边到左边的边)
这就引入了一种算法,叫Rand Contraction算法,这个算法的核心是一个while循环
只要图中的顶点数大于2,就进入循环
1,随机选择图中的一条边,假设边的两个顶点为u和v
2,将这两个顶点u和v融合成一个单独的顶点
3,如果有自循环,就删除掉
最后循环体外,按照只剩下两个顶点的情况进行切割
直接看例子:
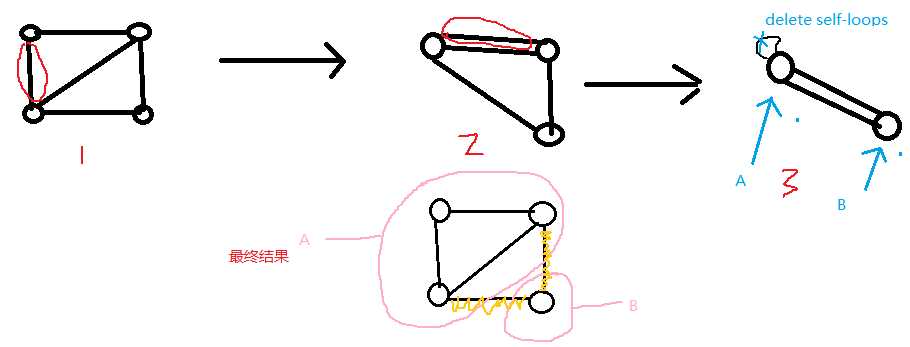
其中红线圈表示每次while循环迭代选择的边,该例子中此种切割方案经过的边最少,为2
下面我们来看另外一种切割方案
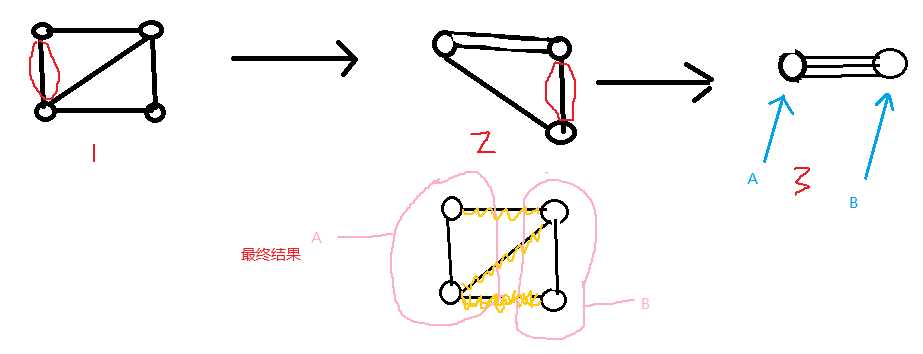
在第二次迭代的时候,我们选择了一条不同的边,这样我们就得到了不同的结果,毫无疑问,这种切割方案并不是最优的
很多情况下,最优的切割方案并不是只有一种,例如二叉树,切割任意一条边都是最优的切割方案,还有没有对角线的多边形
事实上这种算法成功的概率,(我指的是直接找到的是最小切割方案,忽略其它不是最优切割方案的情况),仅仅是大于等于1/n的平方,这是经过数学证明的
尽管如此,这个算法仍然是有用的。
标签:
原文地址:http://www.cnblogs.com/wjf0/p/5879960.html