标签:
文章部分图片来源于龙心尘老师课件。
首先,在了解树模型之前,自然想到树模型和线性模型有什么区别呢?其中最重要的是,树形模型是一个一个特征进行处理,之前线性模型是所有特征给予权重相加得到一个新的值。而树形模型更加接近人的思维方式。树模型拟合出来的函数其实是分区间的阶梯函数。
其次,需要了解几个重要的基本概念:根节点(最重要的特征);父节点与子节点是一对,先有父节点,才会有子节点;叶节点(最终标签)。
一、决策树
决策树生成的数学表达式:

决策树的生成必须要解决两个问题:
(1) 如何分裂训练数据
如何分裂数据也即分裂准则是什么?树模型都是通过不纯度来分裂数据的,通过比较划分前后的不纯度值,来确定如何分裂。不纯度通俗点理解就是目标变量要分得足够开。另一种理解是分类误差率的一种衡量。下面是不纯度的公式,说实话我也没看懂。。。。
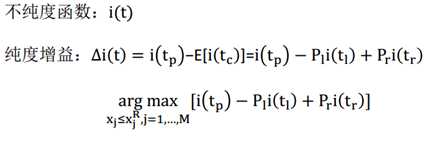
纯度的选取有多种方法,每种方法也就形成了不同的决策树方法,比如ID3算法使用信息增益作为不纯度;C4.5算法使用信息增益率作为不纯度;CART算法使用基尼系数作为不纯度。下面做具体的介绍:
——CART算法:既可以做分类,也可以做回归。只能形成二叉树。
分支条件:二分类问题
分支方法:对于连续特征的情况:比较阈值,高于某个阈值就属于某一类,低于某个阈值属于另一类。对于离散特征:抽取子特征,比如颜值这个特征,有帅、丑、中等三个水平,可以先分为帅和不帅的,不帅的里面再分成丑和中等的。
得分函数(y):就是上面提到的gt(x),对于分类树取得是分类最多的那个结果(也即众数),对于回归树取得是均值。
损失函数:其实这里的损失函数,就是分类的准则,也就是求最优化的准则
对于分类树(目标变量为离散变量):同一层所有分支假设函数的基尼系数的平均。
对于回归树(目标变量为连续变量):同一层所有分支假设函数的平方差损失
对于分类树(目标变量为离散变量):使用基尼系数作为分裂规则。比较分裂前的gini和分裂后的gini减少多少,减少的越多,则选取该分裂规则,这里的求解方法只能是离散穷举。关于基尼系数,可以参考周志华的西瓜书决策树那章,讲得比较简洁,也比较易懂。“直观来说,(数据集D的基尼系数)Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此Gini(D)越小,则数据集D的纯度越高。”
具体这个的计算,我觉得有例子才好理解,下面这个红绿球的例子很好的说明了,如何根据损失函数最小(也就是基尼系数最小)来选取分裂规则。最后GIINs2更小,因此选择它作为分类规则。估计大家有个疑问,就是特征的选择,包括最开始根节点的选取,其实也是同样的方法,决策树方法是会把每个特征都试一遍,然后选取那个,能够使分类分的最好的特征,也就是说将A属性作为父节点,产生的纯度增益要大于B属性作为父节点,则A作为优先选取的属性。

对于回归树(目标变量为连续变量):使用最小方差作为分裂规则。只能生成二叉树。

CART与逻辑回归的比较:
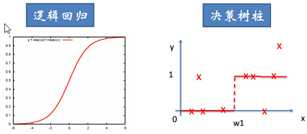
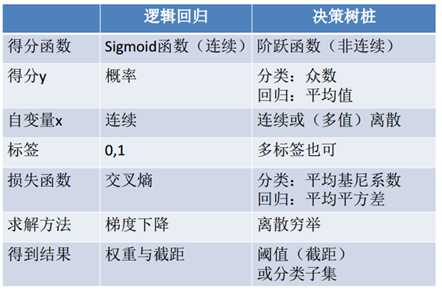

ID3算法:使用信息增益作为分裂的规则,信息增益越大,则选取该分裂规则。多分叉树。信息增益可以理解为,有了x以后对于标签p的不确定性的减少,减少的越多越好,即信息增益越大越好。

C4.5算法:使用信息增益率作为分裂规则,此方法避免了ID3算法中的归纳偏置问题,因为ID3算法会偏向于选择类别较多的属性(形成分支较多会导致信息增益大)。多分叉树。

三种方法对比:

(2) 如何停止分裂
下面这六种情况都会停止分裂。其中第一种其实属于树的完全长成,但这会出现过拟合问题,所有之前很流行一种抑制这种情况的方法,叫树的剪枝,即给分裂准则—基尼系数加上惩罚项,此时树的层数越深,基尼系数的惩罚项会越大。

二、随机森林
尽管有剪枝等等方法,一棵树的生成肯定还是不如多棵树,因此就有了随机森林,解决决策树泛化能力弱的缺点。(可以理解成三个臭皮匠顶过诸葛亮)
而同一批数据,用同样的算法只能产生一棵树,这时Bagging策略可以帮助我们产生不同的数据集。Bagging策略来源于bootstrap aggregation:从样本集(假设样本集N个数据点)中重采样选出Nb个样本(有放回的采样,样本数据点个数仍然不变为N),在所有样本上,对这n个样本建立分类器(ID3\C4.5\CART\SVM\LOGISTIC),重复以上两步m次,获得m个分类器,最后根据这m个分类器的投票结果,决定数据属于哪一类。
随机森林在bagging的基础上更进一步:
1. 样本的随机:从样本集中用Bootstrap随机选取n个样本
2. 特征的随机:从所有属性中随机选取K个属性,选择最佳分割属性作为节点建立CART决策树(泛化的理解,这里面也可以是其他类型的分类器,比如SVM、Logistics)
3. 重复以上两步m次,即建立了m棵CART决策树
4. 这m个CART形成随机森林,通过投票表决结果,决定数据属于哪一类(投票机制有一票否决制、少数服从多数、加权多数)
关于调参:1.如何选取K,可以考虑有N个属性,取K=根号N
2.最大深度(不超过8层)
3.棵数
4.最小分裂样本树
5.类别比例
标签:
原文地址:http://www.cnblogs.com/fionacai/p/5894142.html