标签:
现在有一个长度为n的数组A,另外还有一个整数k。数组下标从1开始。
现在你需要把数组的顺序重新排列一下使得下面这个的式子的值尽可能小。
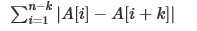
特别的,你也可以不对数组进行重新排列。
单组测试数据。
第一行包含两个整数n,k (2≤n≤3*10^5, 1≤k≤min(5000,n-1))。
第二行包含n个整数 A[1],A[2],...,A[n] (-10^9≤A[i]≤10^9)。
输出答案占一行。
3 2
1 2 4
1
这题一看题就是把数组分成了k组,k组分别怎么排列后求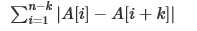 ,然后求k组之和最小,k组里面有n%k组有n/k + 1 个数,有k - n %k 个有n/k个,一个组内部怎样最小当然是按从小到大排最小,内部可以消掉,之等于最大值减最小值,所以所有的数排序,求怎样划分成k组能使和最小。dp方程(i表示有n/k个数):dp[i][j] = min(dp[i-1][j] + a[i * (n/k) + j * (n/k + 1) -1] - a[(i-1) * (n/k) + j * (n/k + 1) -1],dp[i][j-1]+a[i * (n/k) + j * (n/k + 1) -1] - a[i * (n/k) + (j -1)* (n/k + 1) -1],);
,然后求k组之和最小,k组里面有n%k组有n/k + 1 个数,有k - n %k 个有n/k个,一个组内部怎样最小当然是按从小到大排最小,内部可以消掉,之等于最大值减最小值,所以所有的数排序,求怎样划分成k组能使和最小。dp方程(i表示有n/k个数):dp[i][j] = min(dp[i-1][j] + a[i * (n/k) + j * (n/k + 1) -1] - a[(i-1) * (n/k) + j * (n/k + 1) -1],dp[i][j-1]+a[i * (n/k) + j * (n/k + 1) -1] - a[i * (n/k) + (j -1)* (n/k + 1) -1],);
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define MAXN 300001 5 #define INF 1<<30 6 using namespace std; 7 8 int dp[5001][5001]; 9 int a[MAXN]; 10 11 int main() 12 { 13 int n,k; 14 scanf("%d%d",&n,&k); 15 for(int i = 0; i < n; i++) 16 scanf("%d",a+i); 17 sort(a,a+n); 18 int x1 = k - n % k; 19 int x2 = n % k; 20 k = n/k; 21 dp[0][0] = 0; 22 for(int i = 1; i <= x1; i++) 23 dp[i][0] = dp[i-1][0] + a[i* k - 1] - a[(i-1) * k]; 24 for(int j = 1; j <= x2; j++) 25 dp[0][j] = dp[0][j-1] + a[j * (k+1) -1 ] - a[ (j-1) * (k + 1)]; 26 for(int i = 1; i <= x1; i++) 27 for(int j = 1; j <= x2; j++) 28 { 29 int k0 = (i-1) * k + j *( k + 1); 30 int k1 = i * k + (j - 1)* ( k + 1 ); 31 dp[i][j] = min((dp[i-1][j] + ((k0 + k) > n ? 0 :(a[k0 + k - 1] - a[k0]))), 32 (dp[i][j - 1] + ((k1 + k + 1) > n ? 0 : (a[k1 + k] - a[k1])))); 33 } 34 printf("%d\n",dp[x1][x2]); 35 return 0; 36 }
标签:
原文地址:http://www.cnblogs.com/yutingmoran/p/5901495.html