标签:
链接:http://bak3.vjudge.net/problem/UVA-10048
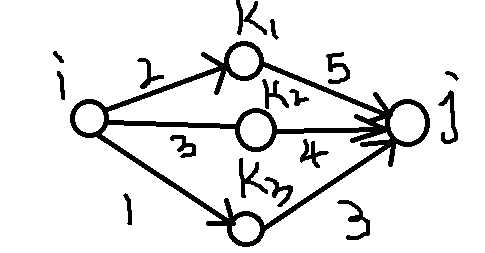
分析:把Floyd算法里的加法改成max。因为不管是floyd算法还是dijkstra算法,都是基于这样一个事实:对于任意一条至少包含两条边的路径i->j,一定存在一个中间点k,使得i->j的总长度等于i->k与k->j的长度之和。对于不同的点k,i->k和k->j的长度之和可能不同,最后还需要取一个最小值才是i->j的最短路径。把刚才推理中“之和”换成“取最大值”,推理仍然适用。
1 #include <cstdio> 2 #include <algorithm> 3 using namespace std; 4 5 const int maxn = 100 + 5; 6 const int INF = 1000000000; 7 int c, s, q, d[maxn][maxn]; 8 9 int main() { 10 int u, v, w, kase = 0; 11 while (scanf("%d%d%d", &c, &s, &q) == 3 && (c || s || q)) { 12 for (int i = 0; i < c; i++) { 13 d[i][i] = 0; 14 for (int j = i + 1; j < c; j++) 15 d[i][j] = d[j][i] = INF; 16 } 17 for (int i = 0; i < s; i++) { 18 scanf("%d%d%d", &u, &v, &w); u--; v--; 19 d[u][v] = min(d[u][v], w); 20 d[v][u] = d[u][v]; 21 } 22 for (int k = 0; k < c; k++) 23 for (int i = 0; i < c; i++) 24 for (int j = 0; j < c; j++) 25 d[i][j] = min(d[i][j], max(d[i][k], d[k][j])); 26 if (kase) printf("\n"); 27 printf("Case #%d\n", ++kase); 28 while (q--) { 29 scanf("%d%d", &u, &v); u--; v--; 30 if (d[u][v] >= INF) printf("no path\n"); else printf("%d\n", d[u][v]); 31 } 32 } 33 return 0; 34 }
标签:
原文地址:http://www.cnblogs.com/XieWeida/p/5903567.html