标签:
PCA作用:
降维,PCA试图在力保数据信息丢失最少的原则下,用较少的综合变量代替原本较多的变量,而且综合变量间互不相关,减少冗余以及尽量消除噪声.
PCA数学原理:
设 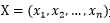 是
是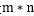 维向量
维向量
想经过线性变换得到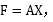 其中F的各行向量相互独立,即
其中F的各行向量相互独立,即
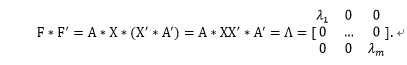
由于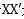 是实对称矩阵,因此存在正交矩阵A满足以上关系,令
是实对称矩阵,因此存在正交矩阵A满足以上关系,令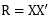 ,即得
,即得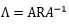 ,得
,得
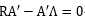
只根据第一列得出的方程为:
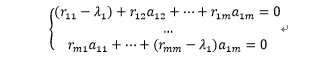
即
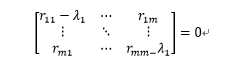
即
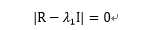
显然,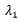 是相关系数矩阵的特征值,
是相关系数矩阵的特征值,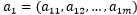 是相应的特征向量.
是相应的特征向量.
根据第二列、第三列等可以得到类似的方程,于是
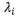 是方程
是方程
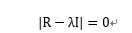
的p个根,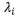 为特征方程的特征根,
为特征方程的特征根,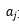 是其特征向量的分量.
是其特征向量的分量.
PCA的计算步骤:
假设样本观测数据矩阵为:
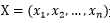 ,
,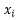 为n个样本在第i个属性上的观测值,是一个列向量
为n个样本在第i个属性上的观测值,是一个列向量
1.对原始数据标准化处理(0均值化处理)
2.计算样本相关系数矩阵
3.计算协方差矩阵的特征值和特征向量
4.选择重要的主成分,并写出主成分表达式
5.计算主成分得分
6.根据主成分得分的数据,做进一步的统计分析.
最大方差理论:
(1)、在信号处理中认为信号具有较大的方差,噪声具有较小的方差,信噪比就是信号与噪声的方差比,越大越好.因此,选择具有较大方差的特征值维度.
(2)、最小特征根接近于零,说明存在多重共线性问题
判断主成分的个数:
最常见的是基于特征值的方法,每个主成分都与相关系数矩阵的特征值 关联,第一主成分与最大的特征值相关联,第二主成分与第二大的特征值相关联,依此类推.
1、Kaiser-Harris准则建议保留特征值大于1的主成分,特征值小于1的成分所解释的方差比包含在单个变量中的方差更少.
2、Cattell碎石检验则绘制了特征值与主成分数的图形,这类图形可以展示图形弯曲状况,在图形变化最大处之上的主成分都保留.
3、可以进行模拟,依据与初始矩阵相同大小的随机数矩阵来判断要提取的特征值.若基于真实数据的某个特征值大于一组随机数据矩阵相应的平均特征值,那么该主成分可以保留.该方法称作平行分析.
优缺点:
优点:首先它利用降维技术用少数几个综合变量来代替原始多个变量,这些综合变量集中了原始变量的大部分信息.其次它通过计算综合主成分函数得分,对客观经济现象进行科学评价.再次它在应用上侧重于信息贡献影响力综合评价.
缺点:
1、在PCA中,首先应保证所提取的前几个主成分的累计贡献率达到一个较高的水平(即变量降维后的信息量须保持在一个较高水平上),其次对这些被提取的主成分必须都能够给出符合实际背景和意义的解释(否则主成分将空有信息量而无实际含义).
2、主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义那么清楚、确切,这是变量降维过程中不得不付出的代价.因此,提取的主成分个数m通常应明显小于原始变量个数p(除非p本身较小),否则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”.
#################R语言########################
法1:
data=USArrests
data<-scale(data)
#prcomp()####:主成分分析,通过奇异值分解做主成分分析,而不使用协方差矩阵的特征根;
dt<-princomp(data)####主成分分析 可以从相关阵或者从协方差阵做主成分分析;
summary(dt)####提取主成分信息 loadings=T显示主成分分析或因子分析中载荷的内容,提取主成分对应的特征向量;
loadings(dt)####载荷矩阵,查看每个变量对主成分的贡献度;
#predict()############3预测主成分的值;
screeplot(dt,type="lines")####画出主成分的碎石图;
biplot(dt)#######画出数据关于主成分的散点图和原坐标在主成分下的方向,双重信息图#################biplot,查看各个变量的表现.
法2(细节过程):
d=read.table("clipboard",header=T) #从剪贴板读取数据
sd=scale(d) #对数据进行标准化处理
d=read.table("clipboard",header=T) #从剪贴板读取标准化数据
pca=princomp(d,cor=T) #PCA函数
screeplot(pca,type="line",mian="碎石图",lwd=2) #画出碎石图
dcor=cor(d) #求相关矩阵
deig=eigen(dcor) #求相关矩阵的特征值和特征向量
deig$values #输出特征值
sumeigv=sum(deig$values)
sum(deig$values[1:2])/k #求前两个主成分的累积方差贡献率
pca$loadings[,1:2] #输出前2个主成分的载荷系数
deig$values[1]/k;deig$values[2]/k; #计算主成分C1、C2的系数b1、b2
C=(b1*C1+b2*C2)/(b1+b2)=q1*C1+q2*C2
s=pca$scores[,1:2] #输出前两个主成分的得分
c=s[1:评价对象的个数,1]*q1+s[1:评价对象的个数,2]*q2
cbind(s,c)
####################Python#########################
from numpy import *
def loadDataSet(fileName,delim=‘\t‘):
fr=open(fileName)
stringArr=[line.strip().split(delim) for line in fr.readlines]
datArr=[map(float,line) for line in stringArr]
return mat(datArr)
def pca(dataMat,topNfeat=9999999):
meanVals=mean(dataMat,axis=0)
meanRemoved=dataMat-meanVals
covMat=cov(meanRemoved,rowvar=0)
eigVals,eigVects=linalg.eig(mat(covMat()))
eigValInd=argsort(eigVals)
eigValInd=eigValInd[:-(topNfeat+1):-1]
redEigVects=eigVects[:,eigValInd]
lowDDataMat=meanRemoved*redEigVects
reconMat=(lowDDataMat*redEigVects.T)+meanVals
return lowDDataMat,reconMat
标签:
原文地址:http://www.cnblogs.com/dudumiaomiao/p/5905725.html