标签:
看syq的代码写出来的,chty_orz
原题:
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
1. 游戏界面是一个长为 n,高为 m 的二维平面,其中有k 个管道(忽略管道的宽度)。
2. 小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
3. 小鸟每个单位时间沿横坐标方向右移的距离为 1,竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度 X,每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度 Y。小鸟位于横坐标方向不同位置时,上升的高度 X 和下降的高度 Y 可能互不相同。
4. 小鸟高度等于 0 或者小鸟碰到管道时,游戏失败。小鸟高度为 m 时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
5≤n≤10000,5≤m≤1000,0≤k<n,0<X<m,0<Y<m,0<P<n,0≤L<H≤m,L+1<H。
这个DP呢代码非常简单,如果看题解的话很容易就写出来了,主要就是状态转移方程要变一下
裸的方程很好推,f[i][j]=min(f[i][j],f[i-1][j-k*x[i]]+k),这样能拿60-70,还是挺实惠的
如果想A掉的话,就要优化这个方程,这个方程搞了三重循环,要把k的内个优化掉
然后有酱紫两个方程f[i][j]=min(f[i][j],f[i-1][j-k*x[i]]+k),f[i][j-x]=min(f[i][j-x],f[i-1][j-x-(k-1)*x]+k-1)
这两个方程就和求等比数列通项公式内样乘上个系数所有的项都往右移了一格,然后减一下,就变成了
f[i][j]=f[i][j-x]+1,所以f[i][j]=min(f[i-1][j-x],f[i][j-x])+1,然后f[i][j]就能O(1)算了
用这个方程推过去就好,要注意处理撞墙和撞顶的情况
最后扫一遍即可
有时候DP复杂度比较高的时候,就可以考虑用一些奇奇怪怪的方式把一些东西约掉,或许我要去学一下斜率优化?
这题我是参考chty的代码写的,他的代码中有这么一段:
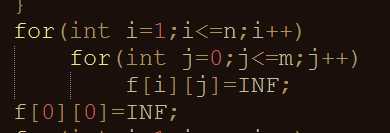
看到这段的时候我大概是这个样子:

所有的f一开始都全设成INF了,min(f[i][j])怎么搞???
然后跟踪了一下才发现原来f[0]中只有f[0][0]被设成INF了,剩下的还是0,因为鸟可以从任意位置开始飞,但是不能从零开始
这题我之前是看过一遍的,再想做的时候就凭上次的记忆直接开始做,没好好看题,甚至题意都曲解了,所以不管什么时候开始做某道题,就算之前看过了,也一定要认真把问题扫一遍
同时也显示出来我考虑不严谨,思维没有覆盖到f[0]
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 using namespace std; 7 int read(){int z=0,mark=1; char ch=getchar(); 8 while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)mark=-1; ch=getchar();} 9 while(ch>=‘0‘&&ch<=‘9‘){z=(z<<3)+(z<<1)+ch-‘0‘; ch=getchar();} 10 return z*mark; 11 } 12 int oo=168430090; 13 int n,m,p,up[11000],down[11000],ding[11000],di[11000]; 14 int f[11000][1100]; 15 int main(){//freopen("ddd.in","r",stdin); 16 memset(ding,0,sizeof(ding)),memset(di,0,sizeof(di)); 17 memset(f,10,sizeof(f)); 18 cin>>n>>m>>p; 19 for(int i=1;i<=n;i++){ up[i-1]=read(),down[i-1]=read(); di[i]=0,ding[i]=m+1;}//顶部也有可能是m,注意是从0到n 20 int _x; 21 for(int i=1;i<=p;i++){ _x=read(); di[_x]=read(),ding[_x]=read();} 22 f[0][0]=oo; for(int i=1;i<=m;i++)f[0][i]=0;//可以从任意高度开始,但不能是0 23 for(int i=1;i<=n;i++){ 24 for(int j=up[i-1];j<=m;j++){ 25 f[i][j]=min(f[i][j],f[i][j-up[i-1]]+1); 26 f[i][j]=min(f[i][j],f[i-1][j-up[i-1]]+1); 27 } 28 for(int j=m-up[i-1];j<=m;j++){ 29 f[i][m]=min(f[i][m],f[i-1][j]+1); 30 f[i][m]=min(f[i][m],f[i][j]+1); 31 } 32 for(int j=di[i]+1;j<=ding[i]-1;j++)if(j+down[i-1]<=m) 33 f[i][j]=min(f[i][j],f[i-1][j+down[i-1]]); 34 for(int j=1;j<=di[i];j++) f[i][j]=oo; 35 for(int j=ding[i];j<=m;j++) f[i][j]=oo; 36 } 37 int bu=p,ans=oo; 38 for(int i=n;i>=1;i--){ 39 for(int j=di[i]+1;j<=ding[i]-1;j++) 40 ans=min(f[i][j],ans); 41 if(ans!=oo) break; 42 if(ding[i]<=m) bu--; 43 } 44 if(bu==p) cout<<1<<endl<<ans<<endl; 45 else cout<<0<<endl<<bu<<endl; 46 return 0; 47 }
标签:
原文地址:http://www.cnblogs.com/JSL2018/p/5905782.html