标签:
无向连通图G 有n 个点,n - 1 条边。点从1 到n 依次编号,编号为 i 的点的权值为W i ,每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ,若它们的距离为2 ,则它们之间会产生Wu
×Wv 的联合权值。
请问图G 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入格式:
输入文件名为link .in。
第一行包含1 个整数n 。
接下来n - 1 行,每行包含 2 个用空格隔开的正整数u 、v ,表示编号为 u 和编号为v 的点之间有边相连。
最后1 行,包含 n 个正整数,每两个正整数之间用一个空格隔开,其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。
输出格式:
输出文件名为link .out 。
输出共1 行,包含2 个整数,之间用一个空格隔开,依次为图G 上联合权值的最大值
和所有联合权值之和。由于所有联合权值之和可能很大,[b]输出它时要对10007 取余。 [/b]
5 1 2 2 3 3 4 4 5 1 5 2 3 10
20 74
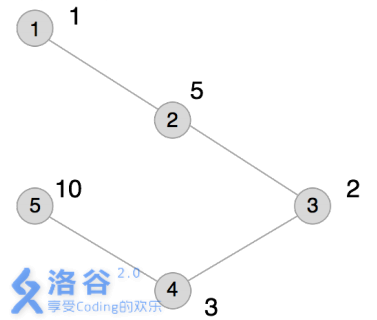
本例输入的图如上所示,距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。
其联合权值分别为2 、15、2 、20、15、20。其中最大的是20,总和为74。
【数据说明】
对于30% 的数据,1 < n≤ 100 ;
对于60% 的数据,1 < n≤ 2000;
对于100%的数据,1 < n≤ 200 , 000 ,0 < wi≤ 10, 000 。
【题目分析】
首先我们可以暴力枚举,理论上来说可以过60的数据,如果rp好的话还可以卡几个,下面是枚举的代码,但是只过了40,wa了两个点
#include<cstdio> #include<cstring> #include<iostream> #include<vector> using namespace std; #define modd 10007 int n; int a[2010]; int ans1=0,ans2=0; bool g[2010][2100]; int main() { scanf("%d",&n); for(int i=1;i<n;i++) { int u,v; scanf("%d%d",&u,&v); g[u][v]=1; g[v][u]=1; } for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { if(g[i][j]) { for(int k=1;k<=n;k++) if(g[j][k]&&k!=i) ans1=max(ans1%modd,a[i]*a[k]), ans2+=a[i]%modd*a[k]%modd; } } printf("%d %d",ans1,ans2%modd); return 0; }
仔细考虑一下,我们为什么要枚举呢
若当前和节点u相连的节点的权值是wi,此时u又新加了个节点m,权值为wx,那么:
ans1为最大值,ans2为总和
ans1=max(ans1,max{wi}*wx);
ans2=ans2+w1*wx+w2*wx+...wn*wx=ans2+∑wi*wx;我们发现,只要记录当前节点所连的点的历史最大值和历史权值之和,就可以O(1)来更新两个答案了。
不过要注意,ans2对于一组关系只计算了一次,别忘了乘2 。
#include<cstdio> #include<iostream> #include<cstring> #include<algorithm> #include<vector> using namespace std; #define maxn 200010 #define mod 10007 int u[maxn],v[maxn]; int a[maxn]; int sum[maxn],maxx[maxn]; int ans1=0,ans2=0; int main() { int n; scanf("%d",&n); for(int i=1;i<=n-1;i++) scanf("%d%d",&u[i],&v[i]); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<n;i++) { ans1=max(ans1,max(a[u[i]]*maxn[v[i]],a[v[i]]*maxn[u[i]])); ans2=(ans2%mod+((a[u[i]]%mod)*(sum[v[i]]%mod))%mod+((a[v[i]]%mod)*(sum[u[i]]%mod))%mod)%mod; sum[u[i]]+=a[v[i]]; sum[v[i]]+=a[u[i]]; maxn[u[i]]=max(maxn[u[i]],a[v[i]]); maxn[v[i]]=max(maxn[v[i]],a[u[i]]); } printf("%d %d",ans1,(ans2*2)%mod); return 0; }
标签:
原文地址:http://www.cnblogs.com/xiaoningmeng/p/5906383.html