标签:
1、 参考书《数据压缩导论(第4版)》 Page 66 2(a),4
2.利用程序huff_enc和huff_dec进行以下操作(在每种情况下,利用由被压缩图像生成的码本)
(a)对Sena、Sensin和Omaha图像进行编码。
解:
| 图像文件名 | 压缩前 | 压缩后 | 压缩比 |
| Sena | 64.0KB | 56.1KB | 1.14 |
| Sensin | 64.0KB | 60.2KB | 1.06 |
| Omaha | 64.0KB | 57.0KB | 1.12 |
压缩比=压缩前/压缩后
则根据压缩比可得:压缩比越大,图片被压缩就越小,占用的内存就越小,就压缩空间越大。
4.一个信源从符号集A={a1,a2,a3,a4,a5}中选择字母,概率为P(a1)=0.15,P(a2)=0.04,P(a3)=0.26,P(a4)=0.05,P(a5)=0.50.
(a)计算这个信源的熵。
(b)求这个信源的霍夫曼码。
(c)求(b)中的代码的平均长度,及其冗余。
解:
(a) 根据公式:H(A)=-P(a1)*log2P(a1)-P(a2)*log2P(a2)-P(a3)*log2P(a3)-P(a4)*log2P(a4)-P(a5)*log2P(a5)
=-0.15*log20.15-0.04*log20.04-0.26*log20.26-0.05*log20.05-0.50*log20.50
=1.818(bit)
(b)信源霍夫曼编码的数树:(概率高的为0低的为1,最右边的是高位)
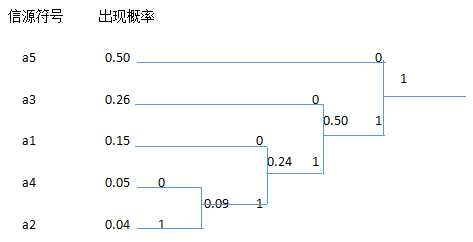
则得出该信源的霍夫曼编码为:
A1=110 A2=1111 A3=10 A4=1110 A5=0
码长:A1:3 A2:4 A3:2 A4:4 A5:1
(c)根据公式:(码长*概率)
代码平均长度:L=3*0.15+4*0.04+2*0.26+4*0.05+1*0.5
=1.83bit
冗余:V=1-N
=1-(H/L*100%)
=1-(1.818/1.83*100%)
=0.0066
2、 思考:为什么压缩领域中的编码方法总和二叉树联系在一起呢?
解:为了使用不固定的码长表示单个字符,编码必须符合“前缀编码”的要求,即较短的编码决不能是较长编码的前缀。
要构造符合这一要求的二进制编码体系,二叉树是最理想的选择。
3、 选做:试将“Shannon-Fano”编程实现。
标签:
原文地址:http://www.cnblogs.com/yxy19880818/p/5908791.html